080100Экономика(МатАнализ и ЛинАлгебра) / Лекции_Линейная_алгебра

z

= r = x2 + y2 .

(11)

arg z = ϕ = arctg

y

0,

x ≥ 0,

(12)

+

x < 0.

x

π,

2.3.1.4. Примеры

Найти модули и аргументы чисел z1 = −2 − 2i , z2 =1 − 3i ,

z3 = −2i .

Решение.

а) z1 = −2 − 2i Re z1 = x1 = −2 < 0, Im z1 = y1 = −2

z

= r =

(−2)2 + (−2)2 = 8 = 2

2, arg z

= ϕ = arctg −2

+ π = π + π = 5π.

1

1

1

1

−2

4

4

б)

z3 = −2i . В том случае,

когда комплексное

–1

y

1

2

число является чисто действительным

или

чисто

O

мнимым, его модуль и аргумент можно определять

x

–1

ϕ3

без привлечения формул (11), (12) непосредственно

из чертежа: ϕ3 = − π , r3 = 2 .

–2

–2i

2

РИС. 2.3.2

z(t) =

eit

.

cost + isin t

Покажем сначала, что z(t) =const . Для этого найдем производную

′

ieit (cost + i sin t) − eit (−sin t + i cost)

=

z (t) =

(cost + i sin t)2

=

eit (i cost + i

2 sin t + sin t − i cost)

=

eit [(sin t − sin t) + i(cost − cost)]

= 0 .

(cost + i sin t)2

(cost + i sin t)2

′

Так как z (t) = 0 , то z(t) =const . Следовательно, если z(t) = x(t) +iy(t) , то

x(t) = C1 и y(t) = C2 . Найдем эти постоянные C1 и C2 .

Чтобы получить C1 и C2 , нужно найти значение z(t) при любом фикси-

рованном значении t , например, при t =0:

z(0) =

ei0

=

1

=1.

Таким образом,

cos0

+ isin 0

1

+ i0

C1 + iC2 =1. Следовательно,

z =1. Тогда

eit

=1 eit = cost + isin t .

cost + isin t

2)

eit1

= ei(t1−t2 ) .

eit2

Пример. Записать число z = −2 3 + 2i в показательной форме.

Решение. x = −2 3 < 0 , y = 2. Следовательно,

r = (−2 3)2 + 22 = 12 + 4 = 16 = 4 ,

ϕ=arctg

2

+ π= −arctg

1

+ π= −π + π=

5π ,

−2 3

3

6

6

5π

i

z = 4e 6 .

2.3.3.4. Умножение и деление комплексных чисел в показательной форме,

формула Муавра. Извлечение корня из комплексного числа

Пусть имеются два комплексных числа, заданных в показательной форме:

z

= r eiϕ1 и

z

2

= r eiϕ2 . Рассмотрим, как выполняются некоторые алгебраические

1

1

2

′ ′

системе. Возникает задача: получить связь между

динаты (x , y ) в новой

′ ′

(x , y ) и(x, y).

1. Рассмотрим первое преобразование системы координат – параллель-

ный перенос.

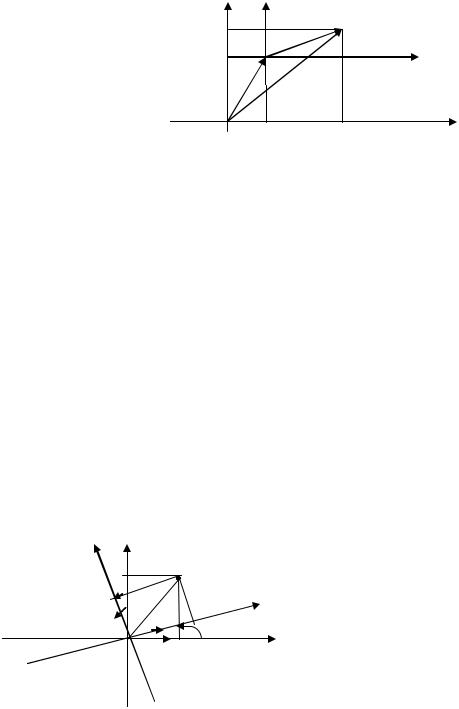
Пусть xOy - старая система координат. Новая система

′ ′

′

получена

x O y

из старой параллельным переносом осей координат, и M (x, y)

координаты точ-

ки в старой системе, а M

′ ′

(x , y ) - в новой системе.

y

y′

M

y

y ′

b

x′

x′

О′

0

a

x

x

Построим

три вектора

′

′

Тогда

OM = OO

′

′

Так

как

OO ,

O M , OM.

+ O M .

′

′

′

′

=(a,b),

OM

=(x, y), то

′

′

O M =(x , y ), OO

(x, y) = (a,b) + (x , y ).

Следовательно,

x = a

+ x′

x′ = x − a

= b

+ y′

y

y′ = y − b

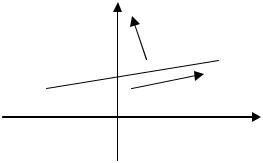
2. Рассмотрим второе преобразование системы координат – поворот осей

координат на угол α, при фиксированном начале координат.

Пусть xOy - старая система координат. Новая система

′

′

получена из

x Oy

старой поворотом осей Ox, Oy на угол α.

y′

y

Рассмотрим точку

M ,

имеющую коорди-

α

M

j

наты (x, y)

в системе

xOy

и координаты

x′

y

′

i

′

′

′

′

α

(x , y )

в системе x Oy .

0

i

x

Построим вектор OM .

РИС. 3.1.2

Тогда OM =(x, y)

– в системе xOy,

следовательно, разложение вектора по ба-

зису на плоскости имеет вид OM = xi + yj, где i , j

- орты в системе xOy.

′

′

′

′

′

′

′ ′

′

′

-

Аналогично OM =(x , y ) в системе

x Oy , т.е. OM = x i

+ y j ,

где i , j

′

′

орты в системе x Oy

,

Отсюда

′

′

′ ′

= xi + yj

(15)

x i

+ y j

37

Если умножить равенство (15) скалярно сначала на

′

′

i

,

а затем на j , и

учесть, что

i

′

i

′

=

i

′

2

=1,

j

′

j

′

=

j

′

2

=1, j

′

i

′

= i

′

j

′

= 0 (i

′

j

′

),

i i′=

i

i′

cos(

i i′)=1 1 cosα =cosα,

j i′ =

j

i′

cos(j i′)

π

= sin α,

=1 1 cos

− α

2

cos(i , j′)

i

j′=

i

j′

=1 1 cos

π

= −sin α,

+ α

2

j j′=

j

j′

cos(j, j′)=1 1 cosα = cosα,

то можно получить

x′ = x cosα + y sin α,

y′ = −x sin α + y cosα.

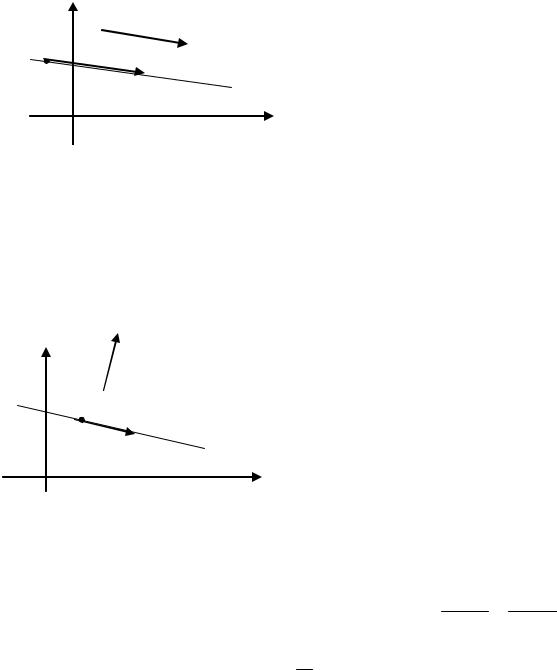
Введем два вектора, определяющие направление.

1)

Вектор S =(m,n) называется

y

направляющим вектором прямой l если он

N

l

параллелен ей (лежит на ней);

S

2)

вектор N = (A, B) называется нор-

мальным вектором прямой l , если он пер-

0

пендикулярен ей, то есть: S l, N l.

РИС. 3.1.3

Найдем виды уравнения прямой, использующие векторы S, N.

3.1.2.2. Уравнения прямой.

1. Дано: точка M 0 (x0 , y0 )

на прямой l и направляющий вектор S =(m,n).

Найти уравнение прямой l.

Пусть M (x, y) – произвольная точка

прямой

l . Тогда

M0M

S –

векторы

y

S

коллинеарны.

Запишем условие

коллинеарности

M 0

M

векторов

M0M =(x − x0 , y − y0 ) и S =(m,n) :

0

x

x − x0

=

y

− y0

(16)

n

РИС. 3.1.4

m

Получили уравнение прямой, которое называется каноническим.

2. Дано: точка M 0 (x0 , y0 )

на прямой l и нормальный вектор N = (A, B).

Найти уравнение прямой.

Если M (x, y) - произвольная точка пря-

y

N

мой l, то M0M N .

Записывая

условие

перпендикулярности

M0

M

векторов

l

M0M =(x − x0 , y − y0 ) и N =(A, B),

0

x Получим второе уравнение прямой

(17)

РИС. 3.1.5

A(x − x0 ) + B( y − y0 ) = 0

y

l

Отношение

S

n

=tgα = k,

n

m

α

0

x

прямой к оси Ox).

РИС. 3.1.6

y − y0 = k(x − x0 )

(18)

S = M1M2 = (x2 − x1, y2 − y1)

- направ-

y

ляющий вектор прямой.

Каноническое уравнение прямой примет

M2

вид

M1

x

− x1

=

y − y1

(19)

x

− x

y

2

− y

x

2

1

1

0

и называется уравнением прямой, про-

РИС. 3.1.7

ходящей через две точки.