
080100Экономика(МатАнализ и ЛинАлгебра) / Линейная алгебра_080100_заоч_1_курс_экз_паспорт
.pdf
R5:
R6:
V1: Векторная алгебра
V2: Линейные операции над векторами
I:
S: Известны координаты точек A = (1; 2) и C = (−3;−3) . Если |
|
|
|||
AB = 2 AC |
− CB , |
||||
то координаты точки B = (x; y) равны … |
|
|
|
|
|
-: (3;4.5) |
|
|
|
|
|
+: (−5;−5.5) |
|
|
|
|
|
-: (−3; −1.5) |
|
|
|
|
|
-: (1;0.5) |
|
|
|
|
|
I: |
|
|
|
|
|
S: Даны векторы |
и |
; если |
|
, то вектор |
|
равен … |
|
|
|
|
|
-: |
|
|
|
|
|
-: |
|
|
|
|
|
+: |
|
|
|
|
|
-: |
|
|
|
|
|
I: |
|
|
|
|
|
S: Если известны координаты вершин |
, |
, |
|
|
|
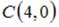 треугольника ABC, то вектор
треугольника ABC, то вектор 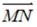 , где М и N – середины сторон АВ и ВС соответственно, равен …
, где М и N – середины сторон АВ и ВС соответственно, равен …
+: 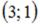 -:
-: 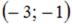 -:
-: 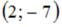
-: 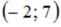 I:
I:
41

. Тогда линейная комбинация
вектором и соответствующим ему
вектором и соответствующим ему
R3:
42
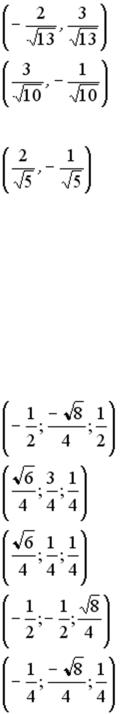
R4: 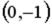
R5: 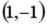
I:
S: Укажите соответствие между заданным вектором и соответствующим ему нормированным вектором (ортом)
L1: 
L2: 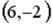
L3:  L4:
L4: 
R1:
R2:
R3: 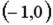
R4:
R5: 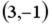
I:
S: Укажите соответствие между заданным вектором и соответствующим ему нормированным вектором (ортом)
L1:  L2:
L2: 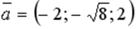
L3: 
R2:
R1:
R4:
R3:
R5:
43

I:
S: Укажите соответствие между заданным вектором и соответствующим ему нормированным вектором (ортом)
L1: 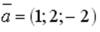
L2: 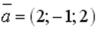
L3: 
R4:
R1:
R3:
R5:
R2:
V2: Скалярное, векторное и смешанное произведения векторов.
I:
S: Направляющим для прямой, заданной уравнением 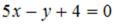 , будет вектор …
, будет вектор …
-: |
|
|
|
|
-: |
|
|
|
|
+: |
|
|
|
|
-: |
|
|
|
|
I: |
|
|
|
|
S: Если |
, |
, |
и точки A, B, C являются вершинами |
|
треугольника, то скалярное произведение векторов |
равно … |
|||
-: 9 |
|
|
|
|
+: 4 |
|
|
|
|
-: 14 |
|
|
|
|
-: 20 |
|
|
|
|
I: |
|
|
|
|
44

и 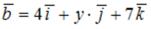 , где
, где  ,
,  и
и  – Известно, что скалярное произведение этих
– Известно, что скалярное произведение этих
этими векторами равен 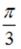 . Тогда значение
. Тогда значение
образованного векторами 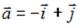 и
и
прямой, заданной как пересечение двух плоскостей
площадь которого равна площади на векторах 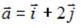 и
и 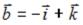 , равна …
, равна …
+:  -: 3
-: 3
I:
45

S: |
равно нулю, |
-:
+:
-:
-: I:
S: |
нулю, |
если
-: -:
-: |
|
+: |
|
I: |
|
S: |
равно нулю, |
если |
|
-: |
|
-: |
|
+: |
|
-: |
|
I: |
|
S: |
нулю, |
-: |
|
+: |
|
-: |
|
-: |
|
I: |
|
S: |
равно |
нулю, если… |
|
-: |
; |
+: |
; |
-: |
; |
-: |
; |
I: |
|
46

S: Даны векторы 
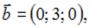
 Смешанное
Смешанное
произведение  Тогда значение m равно …
Тогда значение m равно …
-: 1 +: – 1 -: 7 -: 0
I:
S: Объем треугольной призмы, построенной на векторах
 , равен …
, равен …
+: 8
-: -: 4
-: 16
I:
S: Длина ребра куба, объем которого равен объему параллелепипеда,
построенного на векторах  , равна …
, равна …
-: 1 +: 2 -: 8
-: 3
V1: Аналитическая геометрия на плоскости
V2: Прямоугольные координаты на плоскости
I:
S: Расстояние между двумя точками A(x1; y1) и B(x2 ; y2 ) определяется по формуле …
+: d = 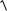
 (х2 − х1)2 + ( у2 − у1)2 -: d = (х2 − х1)2 + ( у2 − у1)2
(х2 − х1)2 + ( у2 − у1)2 -: d = (х2 − х1)2 + ( у2 − у1)2
-: d = 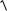
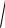 ( y1 − х1)2 + ( у2 − x2 )2
( y1 − х1)2 + ( у2 − x2 )2
-: d = Ах1 + Ву2 + С

 А2 + В2
А2 + В2
I:
S: Точки 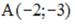 и
и 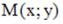 лежат на одной прямой, параллельной оси абсцисс. Расстояние между точками А и М равно 5. Тогда отрицательные координаты точки М равны …
лежат на одной прямой, параллельной оси абсцисс. Расстояние между точками А и М равно 5. Тогда отрицательные координаты точки М равны …
-: 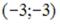 -:
-: 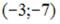 +:
+: 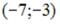
47

ки 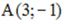 и
и 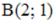 . Тогда координаты точки
. Тогда координаты точки 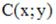 , точке A относительно точки В, равны …
, точке A относительно точки В, равны …
что точка 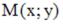 лежит на оси ординат и равноудалена от и
лежит на оси ординат и равноудалена от и 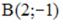 . Тогда точка М имеет координаты …
. Тогда точка М имеет координаты …
ки  и
и 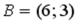 . Тогда абсцисса середины отрезка
. Тогда абсцисса середины отрезка
ки 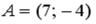 и
и 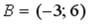 . Тогда ордината середины отрезка
. Тогда ордината середины отрезка
-: 2 +: 1 -: – 1 -: 5 I:
S: Даны точки  и
и  . Тогда ордината середины отрезка
. Тогда ордината середины отрезка 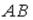 равна …
равна …
+: 1 -: – 1 -: 2 -: 4 I:
48
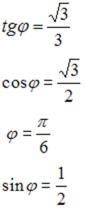
S: Даны точки 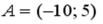 и
и  . Тогда абсцисса середины отрезка
. Тогда абсцисса середины отрезка  равна …
равна …
-: – 9 -: 2 -: – 1 +: – 2
V2: Полярные координаты на плоскости
I:
S: В полярных координатах уравнение луча, проходящего через полюс под углом 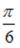 к полярной оси, имеет вид …
к полярной оси, имеет вид …
-:
-:
+:
-: I:
S: Уравнение  в полярных координатах имеет вид …
в полярных координатах имеет вид …
+: 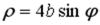 -:
-:  -:
-: 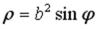
-: 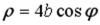 I:
I:
S: Уравнение 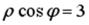 в декартовых координатах имеет вид …
в декартовых координатах имеет вид …
+: 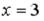 -:
-:  -:
-: 
-: 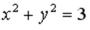 I:
I:
49

S: Уравнение окружности, изображенной на рисунке,
в полярной системе координат имеет вид …
-:  -:
-: 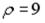 +:
+: 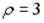
-:  I:
I:
S: На плоскости введена полярная система координат  . Уравнение
. Уравнение
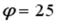 задает на этой плоскости… -: прямую линию
задает на этой плоскости… -: прямую линию
-: окружность радиуса 5 с центром в полюсе -: окружность радиуса 25 с центром в полюсе +: луч
I:
S: Точка 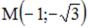 задана в прямоугольной системе координат. Тогда ее
задана в прямоугольной системе координат. Тогда ее
полярные координаты 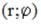
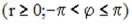 , при условии, что полюс совпадает с началом координат прямоугольной системы, а полярная ось – с положительной полуосью абсцисс и обе системы координат правые, равны …
, при условии, что полюс совпадает с началом координат прямоугольной системы, а полярная ось – с положительной полуосью абсцисс и обе системы координат правые, равны …
+:
-:
-:
-: I:
50
