080100Экономика(МатАнализ и ЛинАлгебра) / Линейная алгебра_080100_заоч_1_курс_экз_паспорт
.pdf
S: Корень уравнения равен …
-: 6 +: 10 -: 2 -: 8 I:
S: Определитель |
равен … |
+: 0 |
|
I: |
|
S: Определитель |
равен … |
+: 0 |
|
I: |
|
S: Определитель |
равен … |
+: 0 |
|
I: |
|
S: Определитель |
|
|
равен … |
|
+: 35 |
|
|
|
|
I: |
|
|
|
|
|
1 −7 |
8 |
|
|
|
|
|||
S: Определитель |
0 |
6 |
3 |
равен … |
|
0 |
0 |
−2 |
|
+: -12 |
|
|
|
|
I: |
|
|
|
|
|
1 −7 |
3 |
|
|
|
|
|||
S: Определитель |
0 |
5 |
0 |
равен … |
|
1 |
0 |
−2 |
|
+: -25 |
|
|
|
|
I: |
|
|
|
|
11
|
|
|
1 −7 3 |
|
|
|
|
||
|
|
|
|
|
|
|
|||
S: Определитель |
|
|
2 |
5 |
4 |
равен … |
|||
|
|
|
0 |
1 |
0 |
|
|
|
|
+: 2 |
|
|
|
|
|
|
|
|
|
I: |
|
|
−1 |
|
|||||
|
|
2 |
|
0 |
|
||||
|
|
|
|||||||
S: Определитель |
|
−16 7 |
8 |
|
|
равен … |
|||
|
|
56 |
4 −28 |
|
|||||
+: 0 |
|
|
|
|
|
|
|
|
|
I: |
|
−3 |
|
|
|
|
|||
|
|
6 |
|
3 |
|
||||
|
|
|
|||||||
S: Определитель |
|
9 |
|
0 |
6 |
равен … |
|||
|
|
|
−12 |
6 |
−6 |
|
|||
+: 0 |
|
|
|
|
|
|
|
|
|
I: |
−2 |
|
|
|
|
||||
|
|
2 |
1 |
|
|
|
|||
|
|
|
|||||||
S: Определитель |
|
−4 |
|
6 −2 |
|
равен … |
|||
|
|
4 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+: 0
V2: Линейные операции над матрицами
I:
S: Даны матрицы |
, |
. Тогда |
матрица |
равна … |
|
-:
-:
+:
12
-: I:
S: Даны матрицы |
, |
, |
. Тогда матрица |
равна … |
|
|
|
-:
-:
-:
+:
I:
S: Дана матрица |
. Если E – |
единичная матрица того же |
размера, что и матрица A, то матрица |
равна … |
|
+:
-:
-:
13
-: I:
S: Если |
, то матрица |
имеет вид... |
-:
+:
-:
-: I:
S: Даны матрицы |
и |
. Тогда |
равно … |
-:
-:
-:
+:
I:
14
S: Даны матрицы |
, |
. Тогда матрица |
равна… |
|
|
-:
-:
+:
-: I:
S: Даны матрицы |
, |
. Тогда матрица |
равна … |
|
|
-:
-:
-:
15
+:
I:
S: Даны матрицы |
, |
. Тогда матрица |
равна … |
|
|
-:
-:
+:
-: I:
S: Если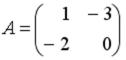 
и 
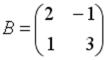, то матрица 
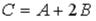имеет вид…
-:
+: 
-: 
-: 
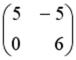
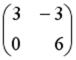
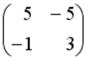I:
16
S: Если |
и |
, то матрица |
имеет вид… |
-:
-:
-:
+:
V2: Произведения матриц
I:
S: Для матриц А и В найдено произведение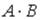 
, причем 
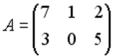. Тогда матрицей В может быть матрица …
-: -: 
+:
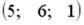
-: I:
S: Для матриц |
|
1 |
2 3 |
|
3 |
0 1 |
|
и транспонированных к ним |
А = |
−1 |
|
, В = |
|
−12 |
|
||
|
|
0 2 |
1 |
|
|
|||
определены произведения …
+: ABT
-: AB
-: A+B
+: AT+B I:
17
|
|
|
1 2 |
|
|
|
1 |
−1 0 |
|
|
S: Для матриц |
А = |
|
−10 |
|
, В = |
|
2 |
0 3 |
|
и транспонированных к ним |
|
|
|
|
|||||||
|
|
|
3 4 |
|
|
|
4 |
−1 2 |
|
|
|
|
|
|
|
|
|
|
определены произведения …
-: ABT
+: BA
-: A+BT
+: ATB I:
S: Для матриц |
, |
и транспонированных к ним |
определены произведения … |
|
|
+: |
|
|
-: |
|
|
+: |
|
|
+: |
|
|
-: |
|
|
I: |
|
|
S: Для матриц |
, |
и транспонированных к ним |
определены произведения … |
|
|
+: |
|
|
+: |
|
|
-: |
|
|
+: |
|
|
-: 
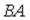
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+: 
-:
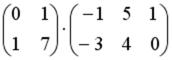
18
+:
+:
-:
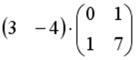
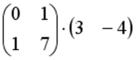
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
-:
+:
-: 
+:
+:
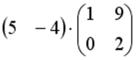
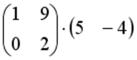
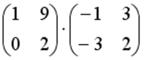
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+:
-:
+:
-:
+:
19
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+:
+:
-:
-:
+:
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+:
+:
-:
+:
-: I:
S:Если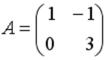 
, 
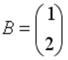, тогда матрица 
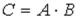имеет вид …
-:
20