
УМК Математика (в 4-х частях) 2 семестр (инженерно-технические направления)
.pdf
|
|
|
|
|
(1 g) (1 |
f ) |
|
|
|
|
|
|
ln f |
|
||||
f g |
f |
|
|
, f g |
, |
f g |
egln f e1 g сводят к раскрытию |
|||||||||||
1 g |
|
|
|
|||||||||||||||
|
|
|
(1 |
f ) (1 g) |
|
|
|
|
|
|
|
|||||||
неопределенностей вида 0 0 или . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) lim |
3x2 2x 8 |
|
0 |
|
|
(3x2 2x 8) |
|
, где |
||||||||||
|
|
|
|
|
|
|
|
lim |
|
|
|
|
||||||
2x |
2 |
3x 14 |
|
(2x |
2 |
3x 14) |
|
|||||||||||
x 2 |
|
|
|
0 |
|
x 2 |
|
|
||||||||||
(3x2 2x 8) (3x2) (2x) (8) 3(x2) 2(x) 0 3 2x 2 1 6x 2,
(2x2 3x 14) |
(2x2) (3x) (14) 2(x2) 3(x) 0 |
2 2x 3 1 4x 3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3x2 2x 8 |
|
|
|
|
0 |
|
|
lim |
|
6x 2 |
|
|
6 2 2 10 |
. |
|
|
|||||||||||||||||||||||||||||
Тогда |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
x 2 2x |
|
|
3x 14 |
|
|
0 |
|
|
x 2 4x 3 |
|
|
4 2 3 11 |
|
|
|
|||||||||||||||||||||||||||||||||||
б) |
|
|
|
e 5x 1 5x |
|
|
0 |
|
|
|
|
|
|
|
|
(e 5x 1 5x) |
, где |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
sin(x |
2 |
) |
|
|
|
|
|
|
|
|
|
|
(sin(x |
2 |
)) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
x 0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
(e 5x 1 5x) (e 5x ) (1) (5x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
5x |
) (e |
u |
|
u 5x ) (e |
u |
)u ux |
|
|
u |
ux |
|
|
|
5x |
( 5x) 5e |
5x |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
(e |
|
|
|
|
|
e |
|
e |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5x) 5(x) 5 1 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5e 5x 5, |
||||||||||||
(sin(x2)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosu ux cos(x2)(x2) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
u x |
2 |
|
(sinu)u ux |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2xcos(x2 ) . |
|
|
|
|
|
|
|
|
e 5x 1 5x |
|
|
|
0 |
|
|
|
|
5e 5x 5 |
0 |
|
|
|
|
|||||||||||||||||||||||||||||||
Тогда |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
. Применяем правило |
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
x 0 |
|
sin(x |
|
) |
|
|
|
|
|
|
0 |
|
x 0 |
2xcos(x |
|
) |
0 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5e 5x 5 |
|
0 |
|
|
|
|
|
|
|
( 5e 5x 5) |
|
|||||||||||||||||||||
Лопиталя ещё раз:lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
, где |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
2xcos(x |
|
|
) |
|
|
|
|
|
x 0 |
(2xcos(x |
|
)) |
|
||||||||||||||||||||||||
( 5e 5x 5) ( 5e 5x ) (5) 5(e 5x ) 0 5 ( 5e 5x ) 25e 5x , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
(2xcos(x |
2 |
)) |
|
2[(x) |
|
cos(x |
2 |
) x(cos(x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
)) ] |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
31

|
|
|
|
cosu |
|
|
|
|
|
|
|
|
|
|
(x) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) 2xsin(x |
|
|||||||||||||
(cos(x2)) |
|
|
|
|
2 |
(cosu)u ux sinu ux sin(x2)(x |
2 ) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=2[1 cos(x2) x( 2xsin(x2))] 2cos(x2) 4x2 sin(x2) . |
|||||||||||||||||||||||||||||
Тогда lim |
5e 5x 5 |
|
0 |
|
|
|
|
|
|
25e 5x |
|
|
|
|
|
|
|
|
25 |
|
25 |
. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2xcos(x |
2 |
) |
|
|
|
|
|
2 |
) 4x |
2 |
sin(x |
2 |
) |
2 0 |
2 |
|
||||||||||||||||||||||||||||
|
|
x 0 |
|
|
|
|
0 |
x 0 2cos(x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
в) lim |
1 |
|
|
1 |
|
|
|
|
. Преобразуем данную неопределённость (при- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
x 1 |
x 1 |
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ведением разности дробей к общему знаменателю) к виду |
0 |
, после чего |
||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
применим правило Лопиталя. Получим |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
x 1 |
|
ln x |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ln x x 1 |
0 |
|
|
|
|
(ln x x 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
=lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
0 |
((x 1)ln x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x 1 |
(x 1)ln x |
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(ln x x 1) (ln x) (x) (1) |
1 |
1 0 |
|
1 x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
((x 1)ln x) (x 1) ln x (x 1)(ln x) 1 ln x
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
||
|
|
ln x x 1 |
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
Тогда |
lim |
|
lim |
|
|
x |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
(x 1)ln x |
0 |
xln x x 1 |
||||||||||||
|
x 1 |
|
|
|
x 1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Применяем правило Лопиталя ещё раз:
(x 1) 1 xlnx x 1 .
|
x |
x |
|
|
|
|
lim |
|
1 x |
|
0 |
. |
|
|
|
|
|
|||
x 1 xln x x 1 |
0 |
|
||||
lim |
1 x |
|
0 |
lim |
(1 x) |
|
, где (1 x) |
(1) (x) 1, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
xln x x 1 |
|
|
|
|
|
|
|
|||||||||||||||||
x 1 |
|
0 |
|
x 1 |
(xln x x 1) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(xln x x 1) (xln x) (x) (1) (x) ln x x(ln x) 1 0 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ln x x |
1 |
|
1 lnx 2. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||
В итоге получим lim |
|
1 x |
0 |
|
|
1 |
1 |
1 |
. |
|||||||||||||||
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
0 2 |
|
||||||||||||||||||
|
|
|
|
x 1 xln x x 1 |
0 |
|
x 1 ln x 2 |
2 |
|
|||||||||||||||
Ответ:
32
|
3x2 2x 8 10 |
|
e 5x 1 5x 25 |
|
|
1 |
|
1 |
|
|
|||||||||
а)lim |
|
|
|
|
|
; б)lim |
|
|
|
|
|
;в)lim |
|
|
|
|
|
|
|
2x |
2 |
3x 14 |
|
sin(x |
2 |
) |
|
|
|
|
|||||||||
x 2 |
|
11 |
x 0 |
|
2 |
x 1 |
x 1 |
|
ln x |
|
|||||||||
51-60. Для указанной функции y f (x) требуется:
а) провести полное исследование функции и построить её график; найти наибольшее и наименьшее значения функции на отрезке [a,b] ;
в) составить уравнение касательной к графику функции в точке x0 .
1
.
2
б)
а) y |
(x 1)2 |
; |
б) y x3 6x2 1, a 1, b 7 ; |
в) y |
|
x2 |
, x0 4. |
|||
x2 2x |
|
|
|
|
||||||
x 1 |
||||||||||
|
|
|
|
|
|
|||||
Для построения графика функции y f (x) нужно:
1)найти область определения функции;
2)найти область непрерывности функции и точки разрыва;
3)исследовать функцию на чётность, нечётность и периодичность;
4)найти точки пересечения графика с осями координат;
5)найти асимптоты графика функции;
6)найти интервалы возрастания и убывания, экстремумы функции;
7)найти интервалы выпуклости, вогнутости и точки перегиба.
Решение.
а1) Находим область определения функции: D(y) x R | x2 2x 0
=( , 2) ( 2,0) (0, ).
а2) Поскольку данная функция является элементарной, то областью её непрерывности является область определения D(y), а точками разрыва явля-
ются точки x 2 и x 0, не принадлежащие множеству D(y), но являю-
щиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва
в точках x 2 |
|
и x 0, вычислив в них односторонние пределы функции: |
||||||||||||||||
lim |
(x 1)2 |
|
|
1 |
|
, |
lim |
(x 1)2 |
|
1 |
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
x 2 0 x2 2x |
( 2) ( 0) |
x 2 0 x2 2x |
|
|
( 2) ( 0) |
|||||||||||||
lim |
(x 1)2 |
|
|
1 |
, |
lim |
|
(x 1)2 |
|
1 |
. |
|||||||
|
|
|
|
|
|
|
|
|||||||||||
x 0 0 x2 2x |
|
|
( 0) 2 |
x 0 0 x2 2x |
|
( 0) 2 |
||||||||||||
Так как односторонние пределы функции в точках x 2 и x 0 - бесконечные, то данные точки являются точками бесконечного разрыва.
а3) Функция не является периодической.
33

Функция y f (x), в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.
Проверяем является ли функция чётной или нечётной. Так как область определения функции D(y) =( , 2) ( 2,0) (0, ) не симметрична отно-
сительно точки x 0, то данная функция – общего вида. а4) Находим точки пересечения графика с осями координат.
Так как x 0 D(y) , то точек пересечения графика с осью Oy нет.
Положим y 0 и решим уравнение |
y |
(x 1) |
2 |
0. Его решением являет- |
||
x |
2 |
|
|
|||
|
|
2x |
||||
ся x 1. Следовательно, точка ( 1,0) - точка пересечения графика с осью
Ox.
а5) Находим вертикальные и наклонные асимптоты графика функции.
Прямая x x0 является вертикальной асимптотой, тогда и только тогда,
когда x0 является точкой бесконечного разрыва функции y f (x).
Так как точки x 2 и x 0 - точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые x 2 и x 0.
Прямая |
y kx b |
является |
наклонной |
асимптотой графика |
функции |
||||||||||
y f (x) |
при x тогда и только тогда, когда одновременно сущест- |
||||||||||||||
вуют конечные пределы: |
lim |
f (x) |
k и |
lim ( f (x) kx) b . |
|
|
|||||||||
|
|
|
|||||||||||||
|
|
|
|
x |
x |
|
|
x |
|
|
|
|
|||
Вычисляем |
|
сначала |
|
|
|
пределы |
при |
|
x : |
||||||
lim |
f (x) |
lim |
(x 1)2 |
|
0 |
k |
1 |
, lim ( f (x) k x) |
lim |
(x 1)2 |
1 b . |
||||
|
|
|
|
|
|||||||||||
x |
x |
x (x2 |
2x)x |
|
|
x |
1 |
x x2 2x |
|
1 |
|||||
|
|
|
|
|
|
||||||||||
В дальнейшем будем иметь в виду следующий часто встречающийся пре-
|
a |
|
|
xn |
a xn 1 |
a |
|
|
|
|
если |
n m |
||
|
0 |
n |
|
|
|
|
|
|
||||||
дел: lim |
|
|
|
1 |
|
a |
0 |
b |
0 |
если |
n m |
|||
|
|
|
|
|
|
|
||||||||
x b |
|
|
xm |
b xm 1 |
b |
|
|
|
|
|
||||
0 |
m |
|
|
0 |
|
если |
n m |
|||||||
|
|
|
|
1 |
|
|
|
|
||||||
Следовательно y k1x b1 0 x 1, т.е. y 1 - наклонная (горизонтальная)
асимптота графика функции при x . |
|
|
|
x : |
||||||
Аналогично |
вычисляем |
пределы |
при |
|
||||||
|
f (x) |
|
(x 1)2 |
|
|
(x 1)2 |
||||
lim |
|
|
lim |
|
0 k2 , |
lim (f (x) k1x) |
lim |
|
|
1 b2 |
|
|
|
|
|||||||
x |
x |
x (x2 2x)x |
x |
x x2 |
2x |
|||||
34
Следовательно y k2x b2 0 x 1, т.е. y 1 - наклонная (горизонтальная)
асимптота графика функции при x .
а6) Определяем интервалы возрастания, убывания, экстремумы функции. Для этого находим первую производную функции:
|
|
|
|
(x |
1) |
2 |
|
|
(x 1) |
2 |
|
|
2 |
2x) (x 1) |
2 |
(x |
2 |
2x) |
|
|
|
|||||||||
y |
|
|
|
|
|
|
(x |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
(x |
2 |
2x) |
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
x |
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2(x 1)(x2 2x) (x 1)2(2x 2) |
2(x 1) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 2x)2 |
|
|
|
|
|
(x2 2x) |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и определяем критические точки функции |
y f (x), т.е. точки xi D(y) в |
|
||||||||||||||||||||||||||||
которых |
f (xi ) 0 |
или f (xi ) |
не существует: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
2(x 1) |
|
0 x 1 0 x 1 D(y) ; |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
(x2 2x)2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y не существует при x2 |
2x 0 x 0 D(y) |
и x 2 D(y). |
|
|||||||||||||||||||||||
Таким образом, единственной критической (стационарной) точкой функции y f (x) является точка x1 1.
Исследуем знак производной y f (x) в интервалах, на которые критиче-
ские точки функции y f (x) разбивают её область определения D(y), и
найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:
x |
( , 2) |
( 2, 1) |
1 |
( 1,0) |
(0, ) |
y |
+ |
+ |
0 |
|
|
|
|
|
|
|
|
y |
возрастает |
возрастает |
0 |
убывает |
убывает |
Так как при переходе слева направо через точку x 1 производная f (x)
меняет знак с «+» на « », то точка x 1 является точкой локального мак-
симума и ymax y( 1) 0 .
а7) Определяем интервалы выпуклости, вогнутости, точки перегиба графика функции. Для этого находим вторую производную функции:
|
|
|
|
|
|
2(x 1) |
|
|
|
|
|
(x |
1) (x |
2 |
2x) |
2 |
(x 1)((x |
2 |
2x) |
2 |
) |
|
|
|||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|
|
||||||||
|
(y ) |
|
2x) |
|
|
|
|
|
|
(x |
2x) |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 (x |
2 |
2x) |
2 |
(x |
1) 2 (x |
2 |
2x)(2x 2) |
|
|
2(3x |
2 |
6x 4) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
3 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
2x) |
|
|
|
|
|
|
(x |
2x) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
35
и определяем точки возможного перегиба y f (x), |
т.е. точки xi D(y) в |
|||
которых f (xi ) 0или f (xi )не существует: y |
2(3x |
2 6x 4) |
, так как |
|
|
|
0 |
||
(x |
|
|||
|
2 2x)3 |
|
||
3x2 6x 4 0 (квадратное уравнение не имеет действительных корней); y не существует при x2 2x 0 x 0 D(y) и x 2 D(y).
Таким образом, функция y f (x) не имеет точек возможного перегиба.
Исследуем знак второй производной y f (x) в интервалах, на которые точки возможного перегиба функции y f (x) разбивают её область опреде-
ления D(y), и найдём интервалы выпуклости, вогнутости, точки перегиба
графика функции. Результаты исследования представим следующей таблицей:
x |
( , 2) |
( 2, 0) |
(0, ) |
|
|
|
|
y |
+ |
|
+ |
|
|
|
|
y |
график вогнутый |
график выпуклый |
график вогнутый |
Точек перегиба нет.
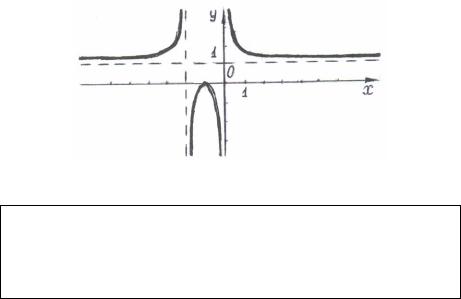
а8)На основании полученных результатов строим график функции (рис.3)
Рис.3.
Наибольшее и наименьшее значения функции y f (x) непрерывной и ку- сочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке [a,b] достигается или в точках xi (a,b) , в которых f (xi ) 0 или f (xi ) не существует, или на концах отрезка.
36

б1) Находим первую производную функции:
y (x3 |
9x2 3) (x3) (9x2) (3) 3x2 18x |
|
|||
и определяем внутренние критические точки функции y f (x), т.е. точки |
|
||||
xi (1,7) в которых |
f (xi ) 0 или |
f (xi ) не существует: |
|
||
y 3x2 18x 3x(x 6) 0 x |
0 |
(1, 7) |
, точек xi (1,7) в которых |
y |
|
|
x |
6 |
(1, 7) |
|
|
не существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функции y f (x) на отрезке [1, 7] является точка
x1 6 .
б2) Вычисляем значения функции y f (x) во внутренних критических точ-
ках |
|
и |
|
|
на |
концах |
|
отрезка |
|
|
[1, 7]: |
|
|
|
|
f (6) 63 9 62 3 105, |
|||||||||||||||||||||||||||||||||||
f (1) 13 |
9 12 3 5 , f |
(7) 73 9 72 |
3 95. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
б3) Сравниваем значения |
f (1) , |
f (6) , f (7) и находим наименьшее и наи- |
|||||||||||||||||||||||||||||||||||||||||||||||||
большее значения функции y f (x) |
на отрезке [1, 7]: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
m yнаим min f (x) f (6) 105 , |
M yнаиб |
max f (x) f (1) 5 . |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
[1,7] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[1,7] |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Уравнение касательной к графику функции y f (x) |
в точке |
M0 (x0 , y0 ) |
|||||||||||||||||||||||||||||||||||||||||||||||||
имеет вид: y y0 |
f (x0 )(x x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
в1) Вычисляем значение функции y f (x) |
в точке x0 4: |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (4) |
|
42 |
|
16 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|||||||||||
в2) Находим первую производную функции: y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
x 1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x( |
|
1) x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
(x |
|
x 1) x |
( x 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
|
|
|
|
3x |
|
|
x 4x |
|
|
|
||||||||||||||||||||
|
|
) ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и вычисля- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)2 |
|
|
|
|
|
|
|
|
|
|
|
1)2 |
|||||||||||||||||
|
|
|
|
|
( |
x |
|
|
|
|
|
|
( |
|
|
x |
|
|
|
|
|
|
|
|
2( |
x |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ем её значение в точке x0 4: f |
|
|
|
|
4 |
4 4 |
4 . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
(4) |
|
|
|
2( |
|
|
1)2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
в3) |
|
Составляем |
|
уравнение |
касательной: |
|
|
y y0 |
f (x0 )(x x0 ) |
|
|||||||||||||||||||||||||||||||||||||||||
y 16 4(x 4) и записываем его в виде |
y kx b : y 4x . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Ответ: а) Рис.3; б) m f (6) 105, |
M |
|
f (1) 5; в) |
y 4x . |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
37

61 – 70. Для указанной функции z f (x, y) |
требуется: а) найти дифферен- |
||||||
циал dz и вторую частную производную |
2 z |
; б) вычислить приближённо |
|||||
x y |
|||||||
|
|
|
|
|
|||
(с помощью первого дифференциала) |
значение функции z f (x, y) в точке |
||||||
|
x |
|
|
|
|
|
|
M(x, y) , если z arctg |
, x 0.03, |
y 0.98. |
|
||||
|
|
||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
||
Первый дифференциал функции z f (x, y) имеет вид dz zxdx zydy.
Частные производные функции z f (x, y) вычисляются по обычным прави-
лам дифференцирования функции одной переменной, в предположении, что если производная берётся по аргументу x (аргументу y ), то другой аргу-
мент y (аргумент x ) считается постоянным.
Решение.
а1) Находим частные производные первого порядка zx и zy функции
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
z arctg |
|
|
|
: z |
|
arctg |
|
|
|
|
|
|
|
|
|
arctgu |
|
|
x |
|
|
|
(arctgu) |
|
u |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
x |
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
u |
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
|
|
|
|
|
|
|
|
|
|
; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 u2 |
x |
|
|
|
|
|
|
2 |
|
|
y |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
y |
|
|
x |
|
|
|
|
y |
|
|
|
|
x2 |
y2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
arctgu |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
zy |
arctg |
y |
|
|
|
u |
|
|
(arctgu)u |
uy |
1 u |
2 uy |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(y) |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
y |
|
|
|
y |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
x |
2 |
y |
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда первый дифференциал dz функции имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
ydx xdy |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
dz zxdx zydy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
x |
2 |
y |
2 |
x |
2 |
y |
2 |
x |
2 |
y |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
38

а2) Вторую частную производную |
|
2z |
|
(или кратко zxy ) находим как пер- |
|||||||||||||||||||||||
x y |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вую частную производную по аргументу y от функции zx |
fx (x, y) : |
|
|
||||||||||||||||||||||||
|
2z |
|
|
|
|
|
|
y |
|
|
|
|
(y)y (x2 y2) y (x2 y2)y |
|
|
||||||||||||
|
|
z |
(z |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|||||||||
|
x y |
xy |
|
x |
y |
|
y |
|
|
|
|
|
|
(x |
y |
) |
|
|
|
|
|
||||||
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
(y)y 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(x2 y2)y (x2 )y |
(y2)y 0 2y 2y |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 (x2 |
y2 ) y 2y |
x2 y2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
2 y2) |
|
|
|
(x2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
y2)2 |
|||||||
Формула для приближённого вычисления значений функции |
z f (x, y) |
в малой |
|||||||||||||||||||||||||
окрестности точки |
M0 (x0, y0 ), в которой функция дифференцируема, имеет вид: |
||||||||||||||||||||||||||
f (x,y) |
f (x0,y0) |
fx(x0,y0) x fy(x0,y0) y , где x x0 |
x , |
y y0 |
y . Форму- |
||||||||||||||||||||||
ла тем точнее, чем меньше значение 
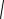 ( x)2 ( y)2 .
( x)2 ( y)2 .
б) Вычисляем значения частных производных zx fx (x, y) , |
zy |
|
fy (x, y) |
и |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
значение |
функции |
|
|
z arctg |
x |
|
|
в |
точке |
|
M |
0 |
(x |
0 |
, y |
0 |
), |
где |
||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x0 x x 0.03 0.03 0 , y0 |
y y 0.98 ( 0.02) 1: |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
f (0,1) 0 , |
fx (0,1) |
1 |
|
|
|
1, fy |
(0,1) |
|
0 |
|
|
|
0. |
|
|
|
|||||||||
|
|
|
|
|
|
|
02 12 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
02 12 |
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда, учитывая, что x 0.03, |
y 0.02, получим: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
f (0.03,0.98) 0 1 |
0.03 0 ( 0.02) 0.03. |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
ydx xdy |
|
2z |
|
|
|
|
x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: а)dz |
, |
|
|
|
|
|
|
|
; б) f (0.03,0.98) |
0.03. |
|
|
||||||||||||||
|
zxy |
|
|
|
|
|||||||||||||||||||||
|
|
x2 y |
2 |
|
x y |
|
|
|
|
(x |
2 y2 )2 |
|
|
|
|
|
|
|
|
|
|
|
||||
71 – 80. Найти локальные экстремумы функции z x3 |
3xy2 15x 12y |
|
|
|||||||||||||||||||||||
(x 0, y 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||||||||||||||||||||||
Для нахождения локальных |
экстремумов |
дифференцируемой |
|
функции |
||||||||||||||||||||||
z f (x, y) |
необходимо: |
1) Найти область определения D(z) функции. |
|
2) |
||||||||||||||||||||||
Найти первые частные производные zx и zy функции. 3) Решить систему
39
уравнений |
(необходимое |
условие |
экстремума) |
zx |
0 |
|
и |
|
найти |
точки |
||||||||||||||||||||||||||||
z |
|
0 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mi (xi , yi ) D(z) (с учётом возможных дополнительных |
|
ограничений на |
||||||||||||||||||||||||||||||||||||
значения аргументов x и |
y ) возможного локального экстремума функции. |
|||||||||||||||||||||||||||||||||||||
4) |
|
|
|
Найти |
вторые |
частные |
производные |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
A(x, y) zxx |
|
B(x, y) zxy , |
|||||||||||||||||||||||||||||||||
C(x, y) zyy ; составить выражение |
D(x, y) A C B2 |
|
и вычислить значе- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Mi |
|
|
|
5) Сделать |
|||||||||||||||||||||||
ния |
|
D |
Mi |
|
и A |
Mi |
в каждой точке |
возможного экстремума. |
||||||||||||||||||||||||||||||
вывод о наличии экстремумов функции z f (x, y), |
используя достаточное |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Mi |
|
|
|
|
|
||||||||||||||||||||||||||||
условие экстремума: если |
D |
Mi 0, то в точке |
|
экстремума нет; если |
||||||||||||||||||||||||||||||||||
|
|
|
|
Mi 0, то в точке Mi |
|
|
|
|
|
|||||||||||||||||||||||||||||
D |
Mi |
0 |
и A |
- локальный минимум; если D |
Mi |
0 и |
||||||||||||||||||||||||||||||||
|
0 , то в точке Mi - локальный максимум; если |
|
|
|
|
|
||||||||||||||||||||||||||||||||
A |
Mi |
D |
Mi |
|
0, то требует- |
|||||||||||||||||||||||||||||||||
ся дополнительное исследование точки |
Mi |
(например, |
по определению). 6) |
|||||||||||||||||||||||||||||||||||
Найти локальные экстремумы (экстремальные значения) функции. |
|
|
|
|
||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y) R |
2 |
|
x 0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1) Находим область определения функции D(z) (x, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
|
||
2) Находим первые частные производные zx |
и zy : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
zx |
(x3 |
3xy2 |
15x 12y)x |
(x3)x |
(3xy2) x (15x)x (12y)x |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(x3)x 3y2(x)x |
15(x)x |
0 3x2 |
3y2 |
1 15 1 3x2 |
3y2 15 ; |
|||||||||||||||||||||||||
zy |
(x3 |
3xy2 |
15x 12y)y |
(x3)y |
(3xy2) y (15x)y (12y)y |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 3x(y2)y |
0 12(y)y |
3x 2y 12 1 6xy 12. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
0 |
|
|
|
|
|
|
2 |
3y |
2 |
15 0 |
|
|||||||
3) |
|
|
|
Составим |
систему |
уравнений |
|
|
x |
|
|
|
|
3x |
|
|
|
|||||||||||||||||||||
|
|
|
z |
y |
|
|
|
|
|
|
6xy 12 0 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3y |
2 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3x |
|
|
и |
решим |
|
её. Получим |
четыре |
решения: |
(1, 2) , |
(2,1) , |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
xy 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
( 1, 2), |
|
( 2, 1). |
Из них |
точками |
возможного |
|
экстремума функции |
|||||||||||||||||||||||||||||||
z f (x, y) |
в области D(z) |
являются только две точки: M1(1, 2) |
и M2 (2,1) . |
|||||||||||||||||||||||||||||||||||
4) Находим вторые частные производные: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
40
