Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Набережночелнинский институт КФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

УМК Математика (в 4-х частях) 2 семестр (инженерно-технические направления)

.pdf

Скачиваний:

Добавлен:

26.02.2016

Размер:

792.05 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

11-21. Вычислить пределы (не пользуясь правилом Лопиталя):

а) lim

3x3 12x 1

б) lim

2 x

x 6

в) lim

tg3x sin3x

г)

x2 x 6

x 2

x 0

3x 2

д)

n! (n 2)!

lim

x 3x 1

n (n 3)! (n 1)!

Вычисление предела lim f (x) , где a x0, , начинают всегда с подстановки

x a

в f (x) предельного значения её аргумента x . В результате могут полу-

читься неопределённости 00, , 0 , , 00 , 1 , 0 , которые рас-

крывают тождественными преобразованиями f (x) такими, чтобы преоб-

разованное выражение получилось определённым. При вычислении пределов используют свойства конечных пределов и бесконечно больших функций, а

также

следующие

известные пределы:

lim a

0xn a1xn 1 an ,

lim

0 ,

lim n!

(n! 1 2 3 n ),

xn a xn 1

x a

lim

sin (x)

lim

tg (x)

lim

arcsin (x)

x a

(x)

x a

(x)

x a

(x)

(x) 0

lim

arctg (x)

lim 1 (x) 1 (x)

e .

x a

(x)

x a

(x) 0

Решение. а) lim

3x3 12x 1

При подстановке вместо переменной x её

предельного значения получим неопределённость . Для её раскры-

тия сначала разделим числитель и знаменатель дроби на x3 (старшую степень переменной x в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим

x3 3

12x 1

lim

3 0 0

0 0

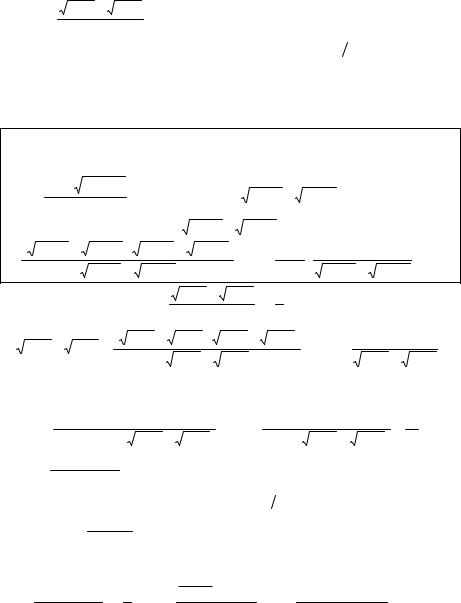
б)

lim

2 x

x 6

При подстановке вместо переменной

её пре-

x 2

x2 x 6

получим неопределённость 0

0 . Для её раскры-

дельного значения x0 2

тия

выделим

числителе

знаменателе

дроби

общий

множитель

вида

(x x0 ) ,

где R -

некоторое число,

т.е. множитель

(x 2) . Затем со-

кратим на него числитель и знаменатель дроби, после чего используем свой-

ства пределов.

1) В квадратном трёхчлене ax2 bx c

множитель выделяют разложением

квадратного

трёхчлена

по

формуле

2 bx c a(x x )(x x

где

b2 4ac

. 2) В выражении (

ax b

cx d )

множитель выде-

1,2

ляют следующим способом:

ax b

cx d

( ax b cx d )(

ax b cx d)

d b

(a c)

ax b

cx d

ax b

cx d

a c

В результате получим

lim

2 x

x 6

x2 x 6

x 2

2 x

x 6 (

2 x

x 6)(

2 x

x 6)

(x 2)

( 2)

2 x

x 6

2 x

x 6

x 6 (x 2)(x 3)

lim

(x 2)( 2)

x 6)

lim

x 6)

1 .

x 2

(x 2)(x 3)(

2 x

x 2 (x 3)(

2 x

в)

lim

tg3x sin3x

При подстановке вместо переменной x её предельно-

x 0

0 . Выделим в числителе мно-

го значения 0 получим неопределённость 0

жители вида

sin (x) ,

где (x) 0

при

x 0 и используем свойства пре-

(x)

делов. Получим

sin3x sin3x

tg3x sin3x

sin3x(1 cos3x)

lim

cos3x

lim

cos3x

x 0

Для раскрытия неопределённостей 00 , содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби

выделяют

сначала

множители

вида:

sin (x)

tg (x)

(x)

arcsin (x)

arctg (x)

, где (x) 0 при

x a , используя формулы триго-

(x)

sin sin 2sin ( )

2 cos ( ) 2 ,

нометрии:

1 cos 2sin2

2 ,

сos cos 2sin ( )

2 sin ( )

2 .

После

чего применяют

свойства пределов, учитывая,

что:

lim

sin

x a

(x) 0

lim

arcsin

lim

arctg

x a

(x) 0

sin3x

sin(3x

3x 2

sin3x 2sin

3x 2

(3x 2)

lim

cos3x

x 0

sin3x

sin(3x 2)

(3x 2)

9 1 1 9

lim

cos3x

x 0

4 1

3x 2 2x

г) lim

? При подстановке вместо переменной x

её предельного

3x 1

значения получим неопределённость 1 .

Для раскрытия неопределённости 1 , возникающей при вычислении предела lim f (x), где f (x) u(x)v(x) , u(x) 0, сначала выражение f (x) представ-

x a
(x)	, где (x) 0 при	x a . После чего
ляют в виде f (x) (1 (x))1 (x)	, где (x) 0 при	x a . После чего

используют свойства пределов, заменяя выражение (1 (x))1 (x) его пре-

дельным

значением

учитывая,

что

(x)

0, если

(x)

(x) .

lim (1 (x))1 (x)

= lim e

(x)

, если

x a

, если

(x) b

3x 2

(x)

Представим

виде

(1 (x))1 (x)

, где

(x) 0

при

3x 1

3x 2

1 (x) (x)

3x 2

3x 1

x ,следующим способом:

3x 1

(x) 2x (x) 2x (x)

(x)

3x 1

3x 2

3x 1

= 1

Тогда

учитывая,

что

3x 1

	3
lim 1

x	3x 1

3x 1		6x		6		6
3	e , lim	6x	lim	6		6	2	, получим

				1
	x 3x 1		x	1		3 0
				3
				3
					x

3x 1

3x 2

3x 1

= lim

lim e3x 1 =e2 .

lim

3x 1

д) lim

n! (n 2)!

(n 3)! (n 1)!

Для вычисления предела lim f (n) , где f (n) представляет собой дробь, чис-

литель и знаменатель которой содержат факториалы натурального числа n, поступают следующим образом. Выделяют в числителе и знаменателе в качестве общего множителя факториал меньшего натурального числа и сокращают на него. В результате получают выражение, предел которого находят рассмотренными выше способами.

Для вычисления данного предела сначала выразим (n 1)!, (n 2)!, (n 3)!

через

n!:

(n 1)! n!(n 1) ,

(n 2)! n!(n 1)(n 2) ,

(n 3)! n!(n 1)(n 2)(n 3), после чего сократим числитель и знаменатель

на n!: lim

n! (n 2)!

lim

n! n!(n 1)(n 2)

(n 3)! (n 1)!

n!(n 1)(n 2)(n 3) n!(n 1)

n!(1 (n 1)(n 2))

3n 1

lim

12n 7

n n!(n 1)((n 2)(n 3) 1)

n n

В результате получили неопределённость [ ]. Для её раскрытия разделим

числитель и знаменатель дроби

n2 3n 1

на n3 (старшую степень

n3 6n2 12n 7

переменной

числителя и знаменателя),

после чего используем свойства

3n 1

пределов. Получим

lim

n n

12n 7

0 0 0

lim

n n2

lim

0 .

6 12

1 0 0 0

n 1

3x3 12x 1

Ответ:

а)

lim

;

б) lim

2 x

x 6

;

x 6

3x 2 2x

x 2

tg3x sin3x

e2; д) lim

n! (n 2)!

в)lim

; г) lim

0 .

x 0

3x 1

n (n 3)! (n 1)!

21-30. Для указанной функции

y f (x)

требуется: а)

выяснить при каких

значениях параметра a функция будет непрерывной; б) найти точки разрыва функции и исследовать их характер. Построить график функции.

					2	,	x 1
x 1,		x 1	x			,	x 1
x 1,		x 1		1
а) у	2	;	б) y			, 1 x 1.
а) у		;	б) y			, 1 x 1.
3 ax		, x 1	x				x 1
				1,			x 1

Решение.

	1		(x),			x x1
		2	(x),	x		x x		2
Точками разрыва функции		2		1				2	являются точ-
Точками разрыва функции	y f (x)								являются точ-

			(x),		x x
		m	(x),		x x		m 1
		m					m 1
ки разрыва функций 1(x), 2(x), , m(x)				в	промежутках ( ,x1),

(x1, x2),…,(xm 1, ) , кроме того, точками возможного разрыва функции

y f (x)

являются точки

x1,x2, ,xm 1

в окрестности которых и в самих

точках функция задаётся разными аналитическими выражениями.

Точка

x x0 является точкой непрерывности функции y f (x) тогда и

только тогда, когда:

lim

f (x)

lim

f (x) f (x0).

x x0 0

а) Поскольку функции 1(x) x 1

и 2(x) 3 ax2 непрерывны в про-

межутках ( ,1)

и (1, )

как элементарные функции, определённые в каж-

дой

точке

данных

промежутков,

то

непрерывность

функции

x 1,

x 1

у 3 ax2, x 1

может нарушиться только в точке её возможного разрыва

x 1.

a из условия непрерывности функции

Определяем значение параметра

y f (x)

точке

x 1:

lim

f (x)

lim

f (x) f (1).

Вычисляя

x 1 0

lim

f (x) ,

lim

f (x) ,

f (1) :

lim

f (x)

lim

(x 1) 2 ,

x 1 0

lim

f (x)

lim

(3 ax2) 3 a,

f (1) 2,

из

условия

непрерывности

x 1 0

2 3 а 2,

находим а 1.

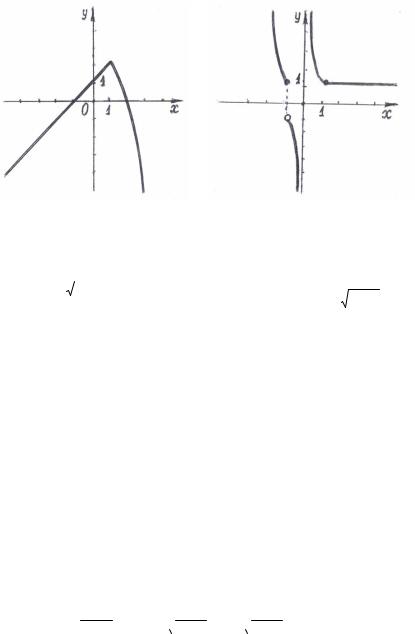
График непрерывной функции

x 1,

x 1

имеет вид изображён-

ный на рис. 1.

3 x2, x 1

б) Функции 1(x) x2

и 3(x) 1

непрерывны в промежутках ( , 1) и

(1, )

как элементарные функции,

определённые в каждой точке данных

промежутков, а функция 2(x) 1 x

в промежутке ( 1,1) имеет точкой раз-

рыва

точку

x 0, в

которой

она

не

определена.

Тогда для

функции

x2,		x 1
	x, 1 x 1 точка		x 0 является точкой разрыва, а точки	x 1 и
y 1	x, 1 x 1 точка		x 0 является точкой разрыва, а точки	x 1 и
	1,	x 1
	1,	x 1

x 1, в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва. Исследуем на непрерывность точки x 1, 0,1:

1)lim f (x) lim f (x) f ( 1)

x 1 0 x 1 0

	lim	f (x) lim x	2	1,	lim f (x)	lim (1 x) 1,
	lim	f (x) lim x		1,	lim f (x)	lim (1 x) 1,	f ( 1) 1
x 1 0		x 1 0			x 1 0	x 1 0
					1 1 1.

Следовательно, точка x 1 - точка разрыва 1-го рода функции y f (x).

lim

f (x)

f (x) f (0)

x 0 0

lim

f (x)

lim

f (x) lim

, f (0) неопределено Сл

x 0 0

x 0 0 x

x 0 0

x 0 0 x

едовательно, точка

x 0 - точка бесконечного разрыва (2-го рода) функции

y f (x).

lim

f (x)

f (x) f (1)

x 1 0

lim f (x) lim (1 x) 1, lim

f (x) lim

1 1, f (1) 1 1 1 1.

x 1 0

Следовательно, точка x 1

- точка непрерывности функции y f (x).

x2,

x 1

График функции y

x, 1 x 1 имеет вид, изображённый на рис.2.

x 1

Ответ: а) Функция у f (x) непрерывна при a 1 (рис.1); б) x 1 - точка разрыва 1-го рода, x 0- точка бесконечного разрыва функции у f (x) (рис.2).

Рис.1

Рис.2

31-40. Найти производную у

f (x) :

xsin

а)

у e4x 3 1 2x ;

б)

;

в) x 2

ln(5x 2)

1 2

Нахождение производной

у y (x)

функции

y y(x)

заданной явно, с

помощью правил дифференцирования:

( f g)

f g ,

( f g) f g f g ,

(Cf ) C f ,

f g f g

( f

g ) f

(ln f )g ,

(x)

F(u)

(u) (x) сводят к нахождению табличных произ-

водных.

u (x)

Производную у y (x)

функции

y y(x)

заданной

параметрическими

уравнениями

x x(t)

параметрическом

виде

по

формуле

находят в

y y(t)

yx (t)

yt (t)

xt (t)

Решение.

а) y e4x 31 2x e4x 31 2x e4x 31 2x , где

eu u ux eu ux e4x (4x) (4x) 4(x) 4 =4e4x ;

e4x

u 4x

3 1 2x

(1 2x)1 3

(u1 3

u 1 2x ) (u1 3)u ux

2 3

(1 2x)

(1) (2x) 0 2(x)

33 (1 2x)2

2e4x (5 12x)

4x 3

Тогда

1 2x

3 (1 2x)

xsin2

(xsin2

3x) ln(5x 2) xsin2

3x (ln(5x 2))

б)

, где

(5x 2)

ln(5x 2)

(xsin2 3x) (x) sin2 3x x(sin2

3x)

(x) 1

(u2

u sin3x ) (u2)u ux

(sin

3x) (sin3x)2

2uux 2sin3x(sin3x)

(sin3x) sinu

ux cosuux

cos3x(3x)

u 3x

(sinu)u

(3x) 3(x) 3 1 3

1 sin2 3x x 2sin3x cos3x 3 sin2 3x 3xsin6x .

(ln(5x 2)) lnu

u 5x 2

(lnu)u ux

u x

(5x 2)

5x 2

(5x 2) (5x) (2) 5(x) 0 5 1 5

5x 2

(sin2 3x 3xsin6x)ln(5x 2) xsin2 3x

Тогда y

5x 2

ln2(5x 2)

(5x 2)(sin2 3x 3xsin6x)ln(5x 2) 5xsin2 3x

(5x 2)ln2(5x 2)

в) Производную функции y f (x), заданной параметрическими уравнения-

x 2

(t)

ми

находим по формуле

yx (t)

, где

(t)

1 2

yt(t)

1 2

(1 2

)

u 1 2

u2 ut

(1 2t ) (1 2t ) (1) (2t ) 2t

ln2

2t ln2

;

2 u

2 1 2t

xt (t) (2t

1) (2t ) (1) 2t

ln2 0 2t ln2 .

ln2

Тогда

yx (t)

2 1 2

ln2

2 1 2t

2t ln2

2 1 2t

41-50. Вычислить пределы, используя правило Лопиталя.

3x2 2x 8

e 5x 1 5x

а)lim

;

б) lim

;

в) lim

3x 14

sin(x

)

x 2

x 0

x 1

ln x


Вычисление предела lim (x) , где a x0, , всегда начинают с подстановки
		x a
в (x) предельного значения её аргумента								x a . Если в результате получа-
ют неопределённость			0	или			, то для её раскрытия применяют правило
		0
Лопиталя: lim	f (x)	lim			f (x)
						, где f (x)		и g(x)- функции, дифференцируе-
						, где f (x)		и g(x)- функции, дифференцируе-
x a g(x)		x a g (x)

мые в окрестности a x0, . В некоторых случаях может потребоваться

неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида:

0 ,

1 ,

0 ,

путём

преобразований:

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.11.2018241.15 Кб5Трудовое право (планы семинаров).doc
#
26.02.2016183.3 Кб6ТСИ для гр2131117,2131121.doc
#
11.11.20194.26 Mб1ТСИ_Лабораторная работа №2.doc
#
16.09.20193.67 Mб48ТЭЦ 440 МВт-мой диплом гост.doc
#
26.02.2016698.88 Кб15умк ЕИ КФУ14изм2.doc
#
26.02.2016792.05 Кб73УМК Математика (в 4-х частях) 2 семестр (инженерно-технические направления).pdf
#
12.11.2019612.86 Кб8УМК Римское право для студентов.doc
#
26.02.20163.04 Mб115УМК ТВиМС.doc
#
16.11.20193.89 Mб7УМК_АЛГЕБРАиГЕОМЕТРИЯ-2011.doc
#
26.02.201648.31 Кб24УМК_Менеджмент инноваций (1).docx
#
26.02.20162.92 Mб122УММ_ДО_Эконометрика.doc