1.3. Формула Симпсона

При аппроксимации интеграла 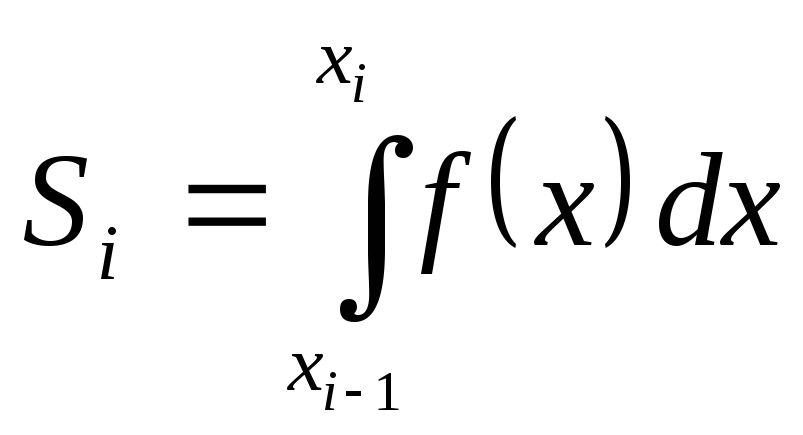заменяем функциюf(x) параболой, проходящей через точки (x_I, f(x_I)), I = i-1, i-0,5, i, т.е. представим приближенно f(x) в виде

Тогда

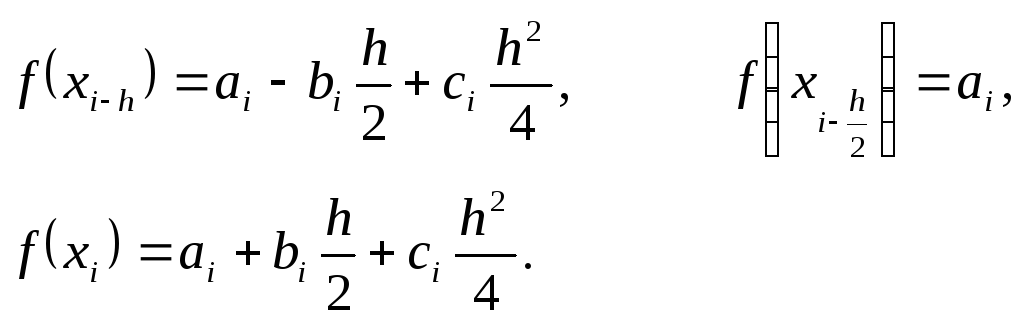(27)

Вычислим

Из (27) получим, что

Таким образом, приходим к приближенному равенству

которое называется формулой Симпсона.

Погрешность этой формулы ψ_i оценивается так [1]:

На всем отрезке [a, в] формула Симпсона имеет вид

Погрешность этой формулы оценивается неравенством:

Из этой оценки видно, что с уменьшением шага h в два раза погрешность формулы Симпсона уменьшается примерно в 16 раз; поэтому значение интеграла, вычисленное с шагом содержащий на один верный знак больше, чем значение интеграла, вычисленное с шагомh. Это правило на практике очень удобно при оценке точности интеграла.

1.4. Задача 1

Между двумя параллельными сбросами инаходится нефтяная залежь В (рис.42) за пределами которой расположены бесконечно простирающая водоносная область. Стрелками показан приток воды из законтурной области. Ширина залежи в = 1000м, толщина пластаh =15м, проницаемость водоносной области k = 0,2·10^-12м², вязкость законтурной водыУпругоемкости β как нефтяной, так и водоносной частей одинаковы, причем β = 2,5·10^-10 Па^-1, вязкость нефти μ_н = 2мПа·С.

Рис. 3

Отбор жидкости из залежи изменяется во времени следующим образом

где – время ввода месторождения в разработку. Требуется определить изменение давления на контуре нефтеносности, т.е. по сравнению с начальным давлением после начала разработки залежи.

Решение. В начале определим пьезопроводность пласта по формуле

Для расчета изменения во времени давления на контуре нефтяной залежи используя аппроксимацию Карслоу и Егеря [2] имеем:

Данный интеграл вычисления одним из методов: метод прямоугольников, трапеции или Симпсона.

1.5. Постановка задачи (круговой контур)

Задача 2. Внешний и внутренний контуры нефтеносности одно-пластового нефтяного месторождения имеют форму, близкую к окружностям (рис.4). Площадь месторождения можно представить в виде круга радиусом R=2000м. Нефтяная залежь окружена обширной водоносной областью, из которой в нефтеносную часть пласта поступает вода при снижении пластового давление р0=20 М Па. По данным гидродинамических

1 2 Рис.4 Контур нефтеносности: 1-внешний, 2-внутренний.

и лабораторных исследований установлено, что средняя проницаемость как нефтеносной, так и водоносной частей пласта одинакова и составляет

0,5·10^-12 м². Толщина пласта в среднем h=10 м,

средняя пористость пласта m=0,3,

начальная нефтенасыщенность S_н=0,45,

насыщенность пласта связанной водой S_св=0,05.

Вязкость нефти и воды в пластовых условиях равны соответственно: .

Коэффициент пьезопроводности .

Добыча жидкость из месторождения изменяется во времени следующим образом: .

где

время ввода месторождения в разработку .

Требуется определить в условиях разработки при упругом режиме в законтурной области пласта изменение пластового давления.