Лекція 2. Поділ прямих у перспективі в заданому відношенні

2.1. Прямі, паралельні картині, поділяються прямо пропорційно на підставі відомого положення в математиці проте, що сторони кута поділяються паралельними прямими пропорційно.

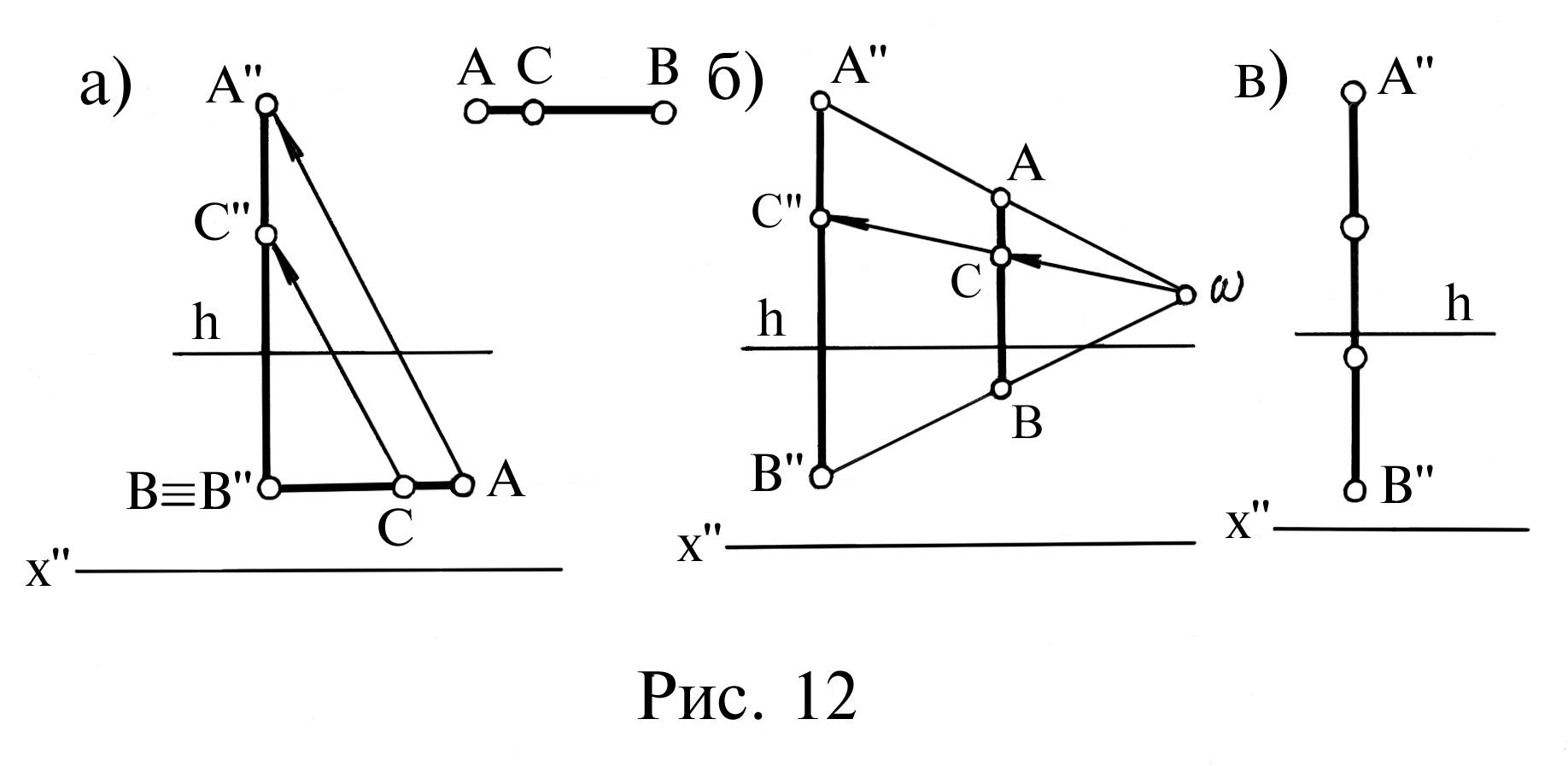
Наприклад, вертикальну (тобто || П") пряму АВ в перспективі треба поділити в заданому відношенні (рис. 12).

Побудова виконується в такій послідовності. До прямої А"В" в перспективі (рис. 12,а) під будь-яким кутом проводиться пряма АВ. З'єднуються кінці відрізків ВВ". Після чого прямою СС", паралельною В"В визначається точка С" у перспективі. Площина ВА"В" – паралельна П", а тому прямі ВВ" і СС" також паралельні між собою, а пряма А"В" поділяється у такому самому відношенні, як і пряма АВ.

Пряму А"В" поділити у заданому відношенні можливо й іншим чином (рис. 12,б). Кінці А", В" з'єднують з довільною точкою Р. Рухаючи паралельно А"В", відрізок АВ сполучають з прямими А"Р, В"Р. Після чого пряма РС визначає точку С".

Якщо пряму, паралельну картині, треба поділити на декілька рівних частин, наприклад, на 3, то це виконується безпосередньо в перспективі, всі частини якої будуть також рівними між собою (рис. 12,в).

2.2. Горизонтальні прямі. а) Поділ прямих на 2, 4, 8, 16 ... частин. Відомо, що, якщо провести діагоналі прямокутника і через точку їх перетину провести пряму КР АВ (рис. 13), то пряма ВС поділиться точкою К на 2 рівні частини.

Якщо після цього кожну половину аналогічно поділити на 2, то можно отримати вже чотири частини і т.д. Тому і в перспективі існує можливість таких дій. Так, якщо пряму С"В" в перспективі треба поділити на 2 рівних частини, то прямокутник 1ВС2 будується в перспективі. Для визначення середини К прямої достатньо провести діагоналі 2В та 1С.

б) Поділ прямих у будь якому відношенні виконується на підставі пропорційного поділу сторін кута паралельними прямими. Так, маємо горизонтальну пряму АВ (рис. 14), яку треба поділити у заданому відношенні. Будуємо кут горизонтальних (рис.14,а) прямих. АВ та АВ || h. Прямі ВВ, 11, 22 – паралельні між собою, а також горизонтальні, точку збігу ω яких на лінії h визначаємо за допомогою прямої ВВ.

Ці побудови можна виконати інакше. Обираємо точка збігу ω у будь- якому місці на лінії горизонту. З’єднуємо А, В з ω. Після чого відрізок АВ, рухаємо паралельно h, доти його кінці не співпадуть з прямими Аω, Вω (рис.14,б).

2.3. Прямі загального положення. Найпростіше поділити у відношенні АСВ перспективу її основи А₁В₁ (рис. 15), як було розглянуто на рис. 14, а потім точку поділу С₁ перенести на перспективу АВ самої прямої (точка С).

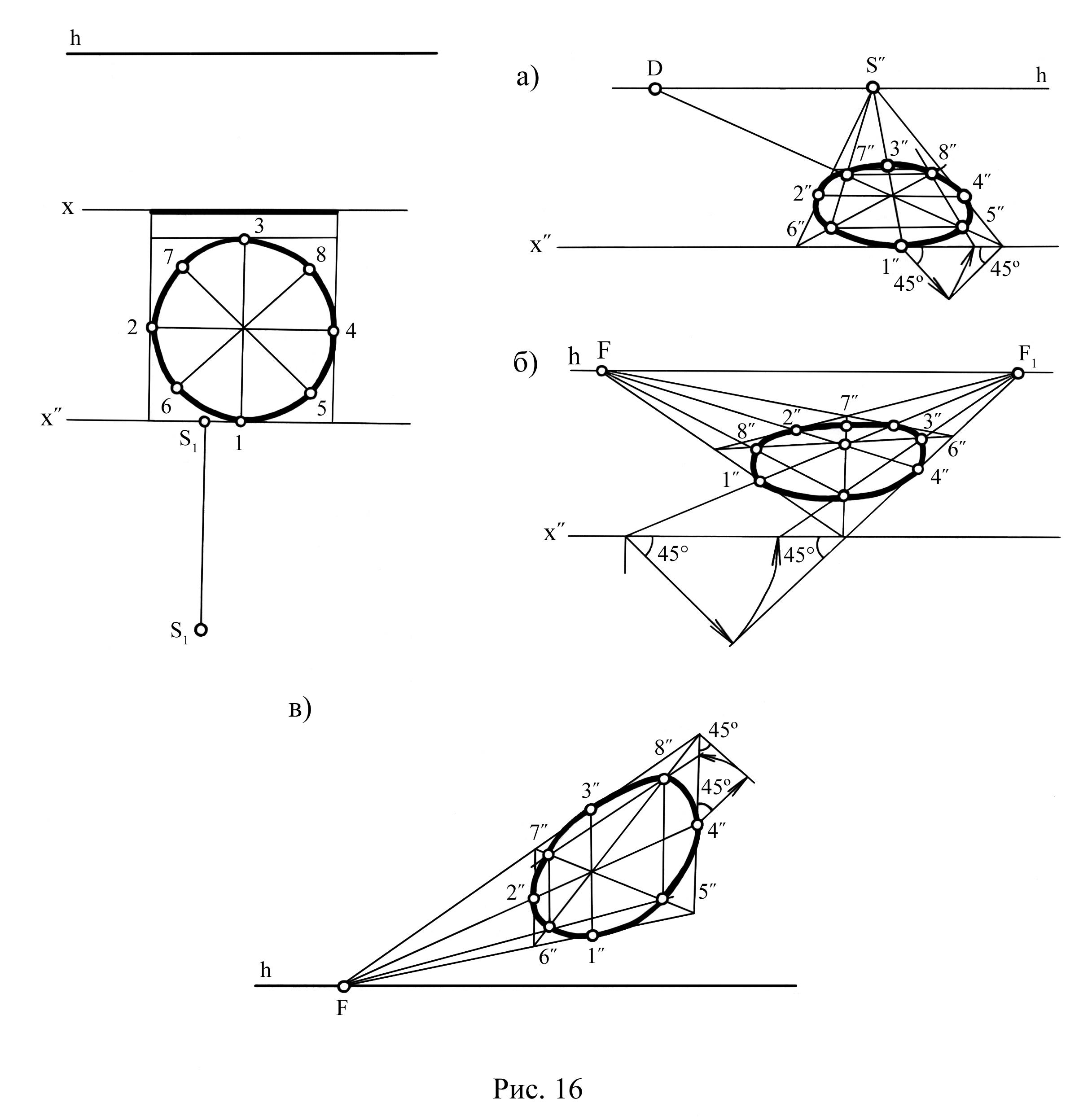
2.4. Побудова кола. Найбільш зручний спосіб побудови перспективи кола за вісьма точками.

На рис. 16,а наведена побудова перспективи кола, розташованого в П₁. Описуємо квадрат, сторони якого паралельні та перпендикулярні картині. Тоді на перспективі кола визначаємо точки 1, 2, 3, 4, як точки дотику сторін квадрата, та точки 5, 6, 7, 8 на діагоналях за допомогою відомого відношення катета до гіпотенузи.

Якщо сторони квадрата розташовані не паралельно картині, то для визначення точок на діагоналях треба половину сторони квадрата винести в площину картини (на х)(рис. 16,б).

Перспектива кола в вертикальній площині (рис. 16,в) будується аналогічно.

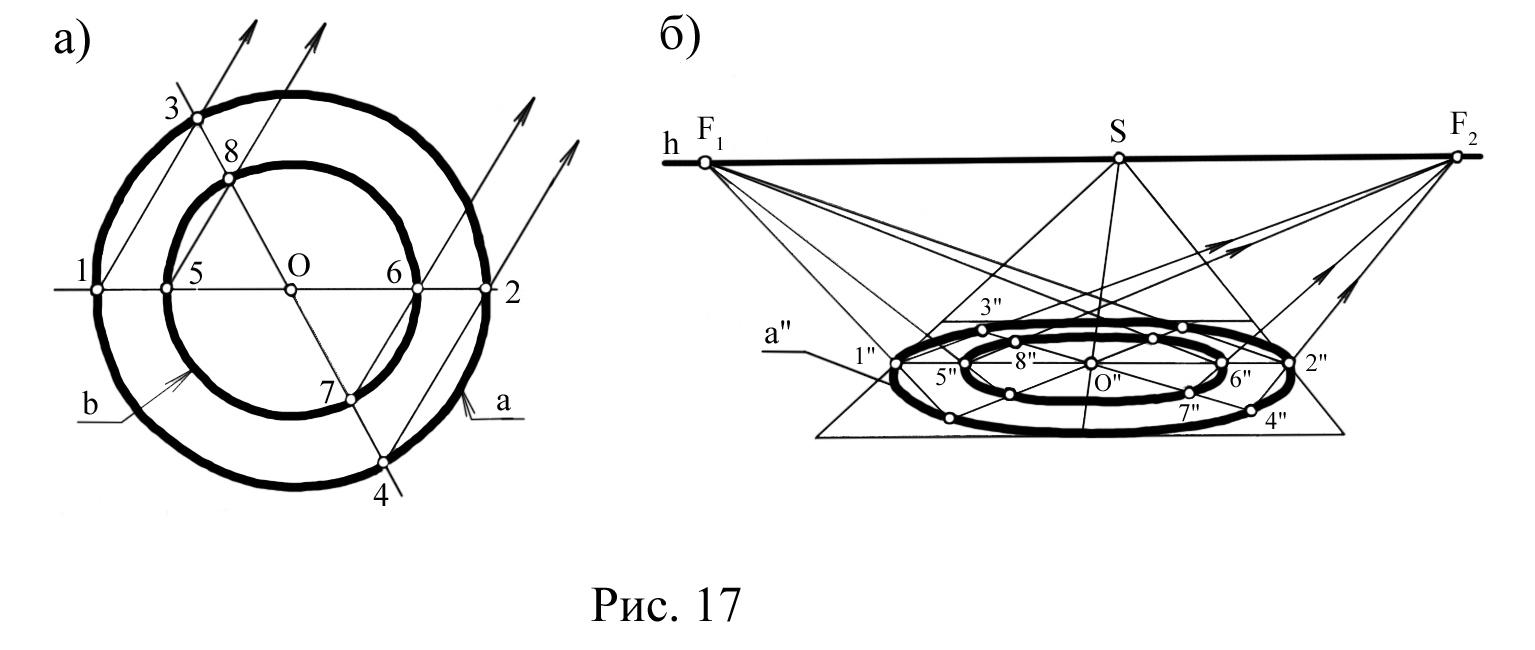
2.5. Перспектива кількох кіл із спільним центром. Якщо маємо перспективу одного кола, то існує можливість побудови іншого кола, розташованого в тій самій площині і з тим самим центром. Так, на рис.17 побудована перспектива горизонтального кола а. Побудуємо інше коло b меншого діаметра із спільним центром. Вирішення будується на паралельності хорд (наприклад, 24 || 67). Точки 5, 6 меншого діаметра визначаються за допомогою поділу прямих.

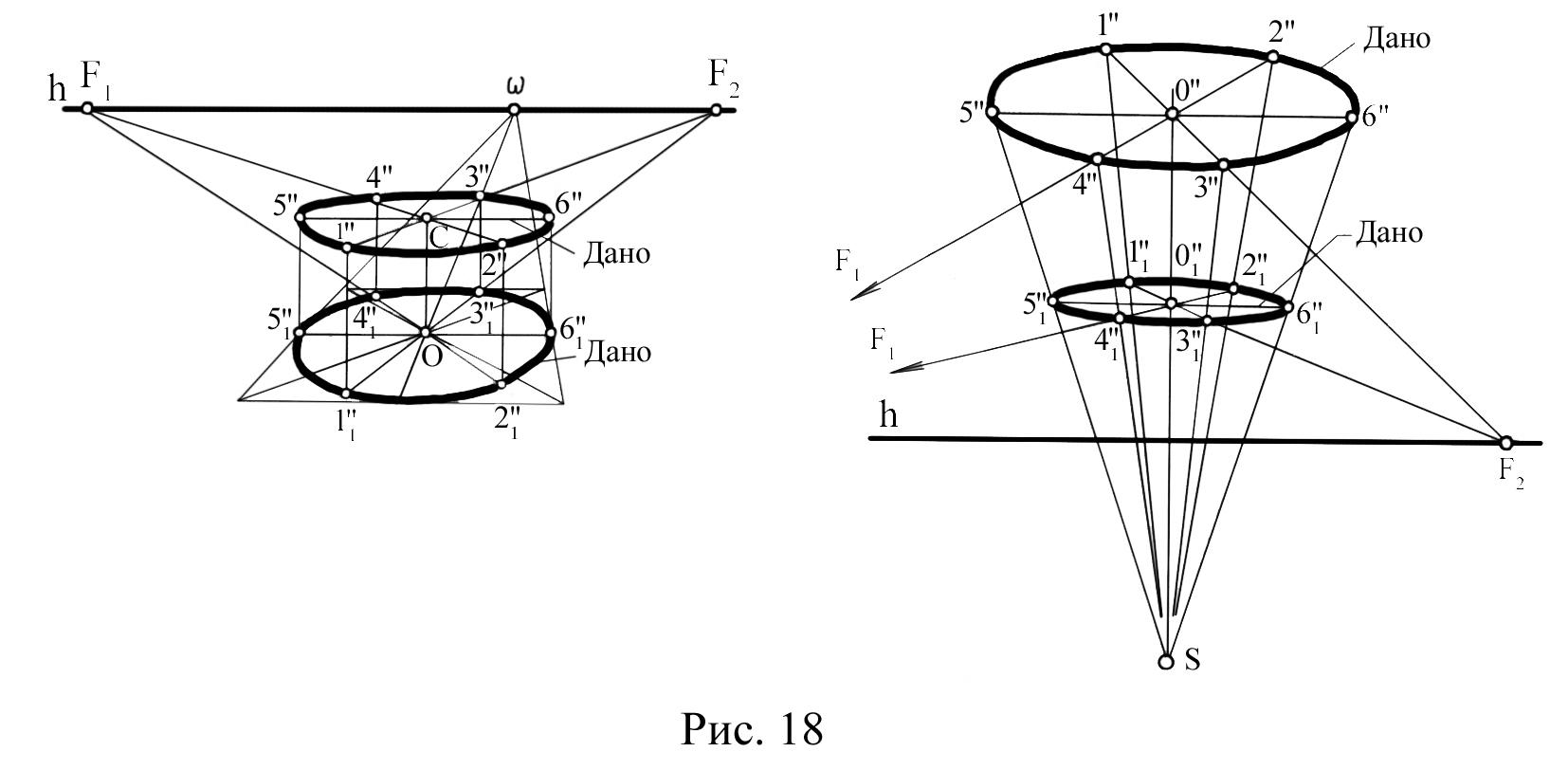
Перспектива кіл однакового діаметра, розташованого у паралельних площинах.

Центри обох кіл знаходяться на вертикальній прямій ОС (рис. 18).

Якщо провести довільний діаметр 12 одного кола, то паралельний йому діаметр другого 34 буде мати спільну точку збігу F.

2.6. Перспектива площини. Так само, як і пряма, площина в перспективі має картинний слід (лінію перетину площини з картиною) та лінію збігу. Лінія збігу визначається як лінія перетину з картиною площини, що проходить через точку зору S паралельно заданій площині. Так, на рис. 19, 20 наведена побудова перспективи прямокутника АВСК, його картинного сліду та лінії збігу.

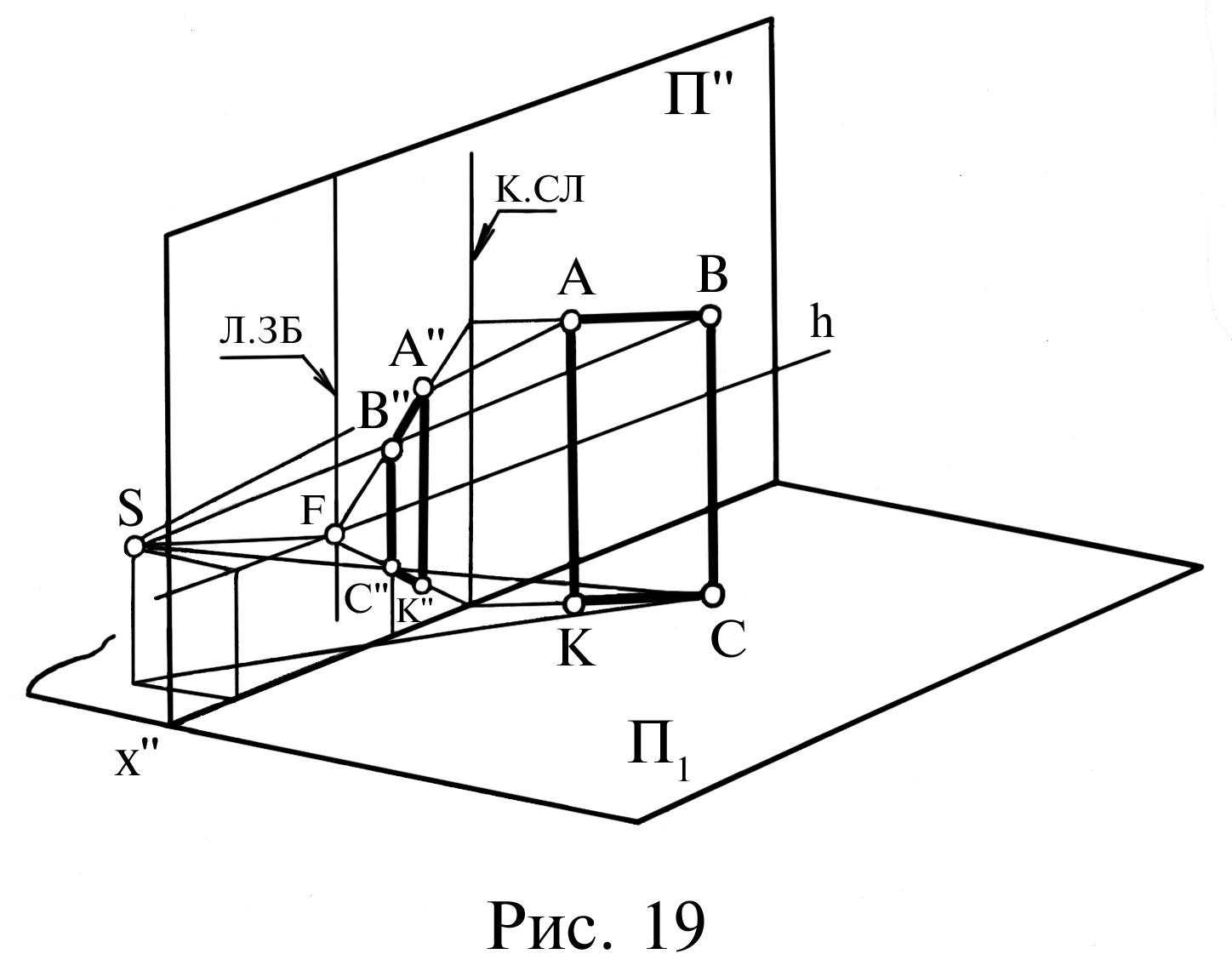
Сторони АК, ВС – паралельні картині, а також паралельні між собою. Тому і в перспективі АК, ВС вони також паралельні. Розмір цих прямих без спотворення проецюється на картинному сліді, який проходить через точку 1. Картинний слід та лінія збігу площини завжди паралельні між собою (лінії перетину двох паралельних площин картиною П).

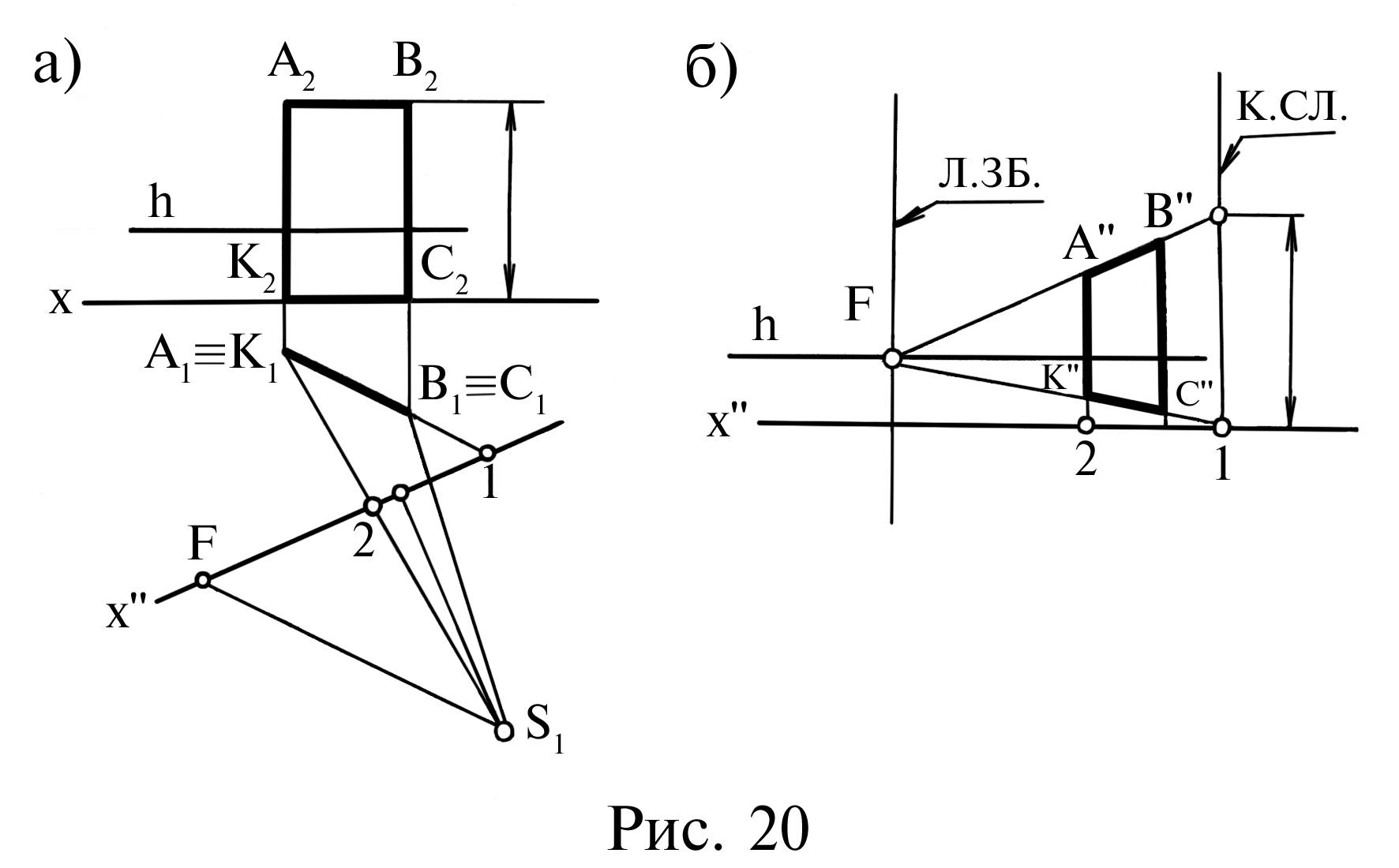
Усі прямі площин будуть мати свої точки збігу та картинні сліди на лініях збігу площини та на її картинному сліді.

Розглянемо рис. 21.

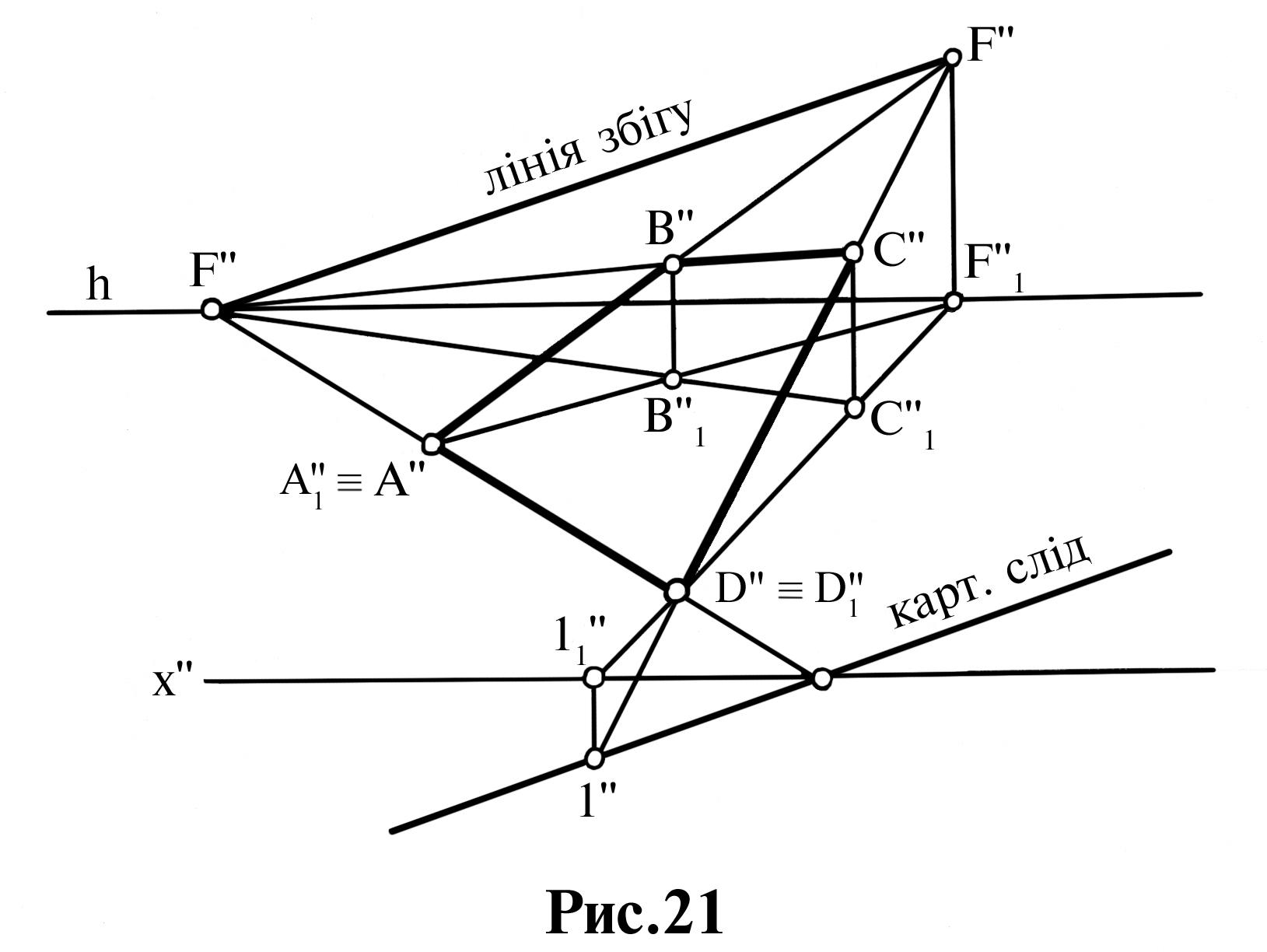
Приклад: на побудованій у перспективі площини ABCD (наведені її перспектива АВСD, та основа А₁В₁С₁D₁) необхідно визначити картинний слід та лінію збігу.

Будь-яка пряма площини (наприклад АВСD) має точку збігу на лінії збігу площини, а свій картинний слід – на картинному сліді площини. Тому, щоб визначити картинний слід площини АВСD та її лінію збігу достатньо визначити картинні сліди та точки збігу будь-яких двох її прямих (наприклад, прямих АD та СD).

Картинний слід та лінія збігу паралельні між собою.

2.7. Перспектива точки визначається як точка перетину двох прямих. Так, на рис. 22 наведено приклад побудови перспективи А точки А простору на підставі її ортогонального креслення.

Апарат проецювання S₁, х, h визначено. Спочатку будується перспектива основи (плану) точки А₁. Вона розташовується у точці перетину в перспективі двох будь-яких прямих (наприклад, a, b), що проходять на П₁ через А₁. Для визначення висоти точки у перспективі використовуємо картинний слід вертикальної площини прямокутника, який проходить через точку А. Висота прямокутника дорівнює висоті точки А і відкладається без спотворення в точці 1 перспективи.

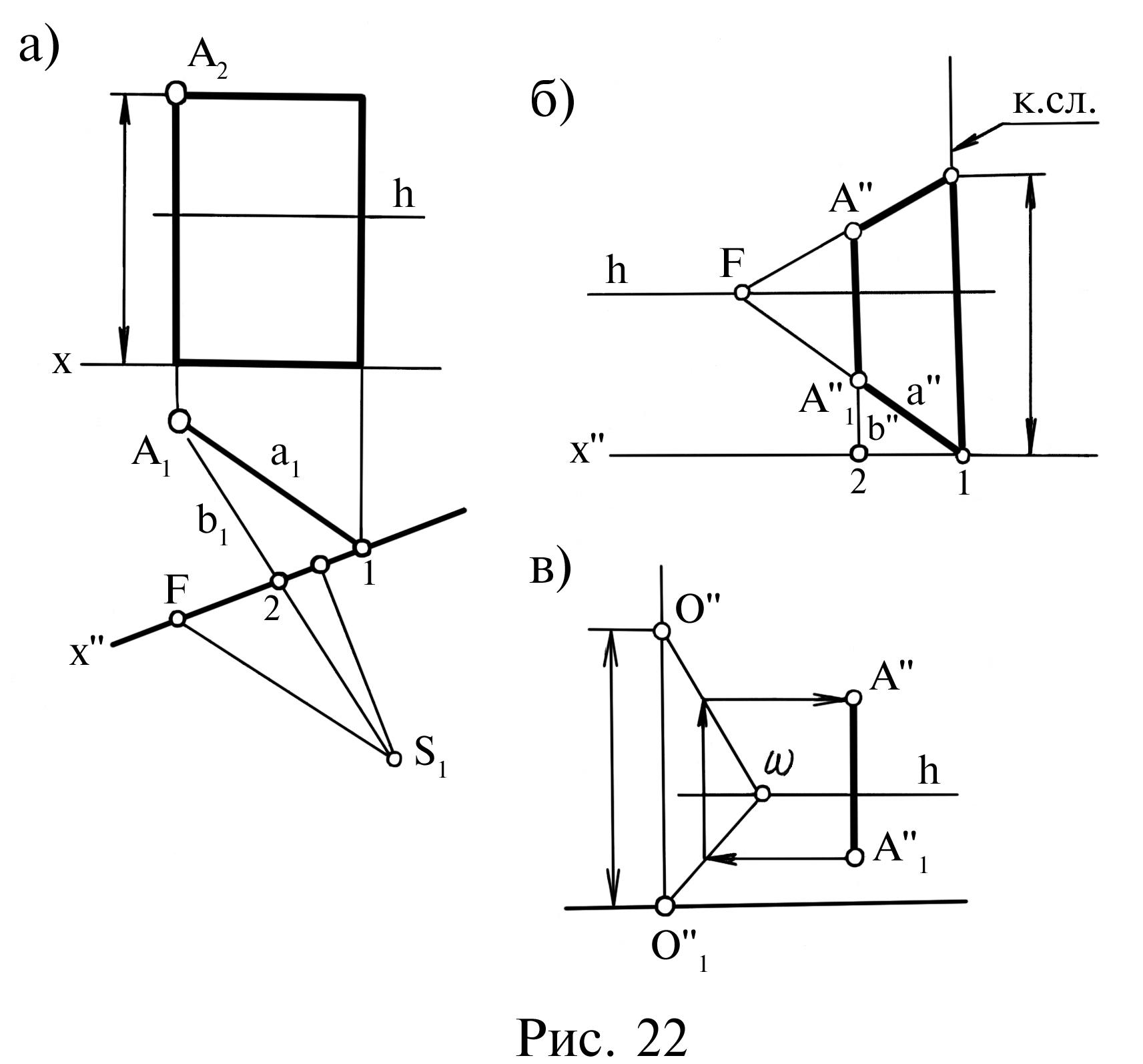
Висоту точки також можна відкласти за допомогою окремо розташованої бокової площини ОО₁ω (рис. 22,в); де ω – точка збігу її горизонтальних прямих, що обирається довільно на лінії h, картинний слід ОО₁ намічаємо також довільно.