I уровень

1.1. Найдите центр масс дуги окружности с плотностью распределения массы

1.2. Найдите работу, производимую силой вдоль указанной линии Г:

1) Г – верхняя половина эллипсаот точкиA(a; 0) до точки B(– a; 0);

2) Г – первая арка циклоиды

1.3. Найдите площадь области D, ограниченной указанным замкнутым контуром L:

1) – эллипс;

2) D – область при пересечении кривых

II уровень

2.1. Найдите массу кривой с плотностью распределения массы

2.2. Найдите центр масс дуги винтовой линии с плотностью распределения массы

2.3. Найдите площадь области D, ограниченной указанным замкнутым контуром L:

1)  – кардиоида;

2) D – область при пересечении кривых

3) D – область, ограниченная осью Ox и одной аркой циклоиды

2.4. Найдите работу, производимую силой вдоль указанной линии Г:

1) Г – один виток винтовой линии

2) Г:

III уровень

3.1. Найдите массу кривой с плотностью распределения массы

3.2. Найдите массу эллипса с плотностью распределения массы

3.3. Найдите массу дуги окружности с плотностью распределения массы

3.4. Найдите площадь области D, ограниченной замкнутым контуром – «декартов лист».

У к а з а н и е :

3.5. Найдите работу, производимую силой вдоль указанной линии Г:

1) Г – отрезок, соединяющий точкиO(0; 0; 0) и M(1; 3; 5);

2) Г – сечение гиперболоидаплоскостьюот точкиA(a; a; 0) до точки

26.4. Независимость криволинейных интегралов

2-го рода от пути интегрирования

Если функции P(x; y) и Q(x; y) непрерывно дифференцируемы в замкнутой ограниченной области D, то все следующие условия равносильны:

1) гдеL – любой замкнутый контур, целиком лежащий в области D;

2) интеграл не зависит от линии интегрирования, соединяющей две данные точки;

3) выражение является полным дифференциалом некоторой однозначной функции;

4) во всех точках области D имеет место равенство

Пример 1. Вычислить криволинейный интеграл 2-го рода по произвольной линии L, соединяющей точки A и B:

1)  где A(1; 1), B(2; 2);

2) гдеA(0; 2), B(1; ln2);

3) гдеA(1; 1), B(3; 3).

Решение. 1) Определим, каковы функции P(x; y) и Q(x; y) в нашем случае:

Проверим справедливость равенства

Следовательно, Делаем вывод, что подынтегральное выражение действительно представляет собой полный дифференциал некоторой функции U(x; y).

Восстановим функцию U(x; y). Для этого пройдем несколько этапов:

а) проинтегрируем по переменной x функцию P(x; y), считая y постоянной величиной:

где представляет собой константу по отношению к переменной x и зависит только от y;

б) продифференцируем полученное выражение по переменной y, считая x константой, и приравняем его к функции Q(x; y):

в) из последнего соотношения найдем и затем после интег­рирования –

г) подставив в выражение из пункта а), получим искомую функцию U(x; y):

Займемся непосредственным вычислением исходного интеграла:

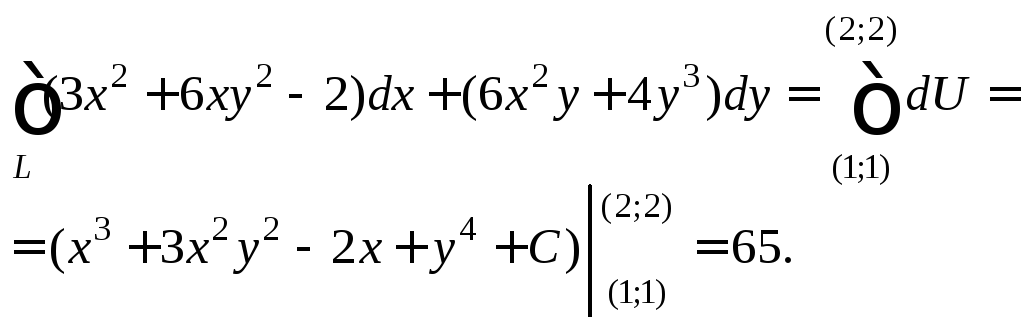
2) Определим, каковы функции P(x; y) и Q(x; y) в заданном случае:

Проверим выполнимость соотношения

Следовательно, Делаем вывод, что подынтегральное выражение действительно представляет собой полный дифференциал некоторой функции U(x; y).

Восстановим функцию U(x; y). Для этого пройдем несколько этапов:

а) проинтегрируем по переменной x функцию P(x; y), считая y постоянной величиной:

где – константа по отношению к переменной x и зависит только от y;

б) продифференцируем полученное выражение по переменной y, считая x константой, и приравняем его к функции Q(x; y):

в) из последнего соотношения найдем и затем после интег­рирования –

г) подставив в выражение из пункта а), получим искомую функцию U(x; y):

Займемся непосредственным вычислением исходного интеграла:

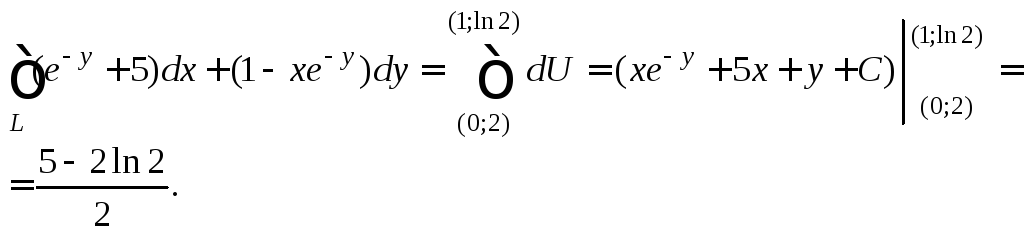
3) Определим, каковы функции P(x; y) и Q(x; y) в нашем случае:

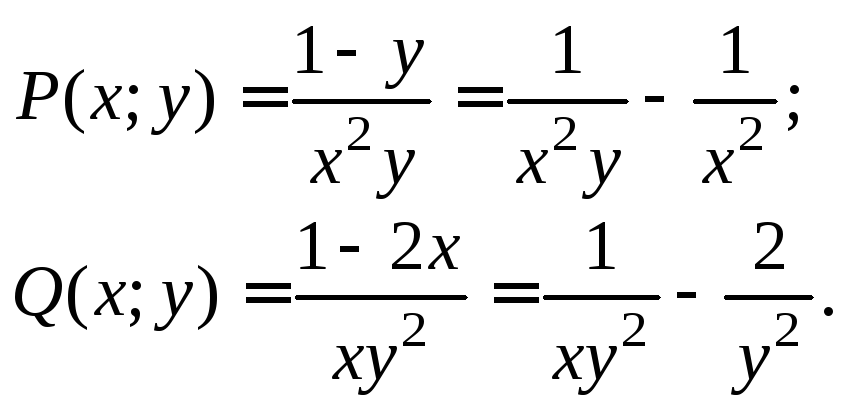
Проверим справедливость равенства

Следовательно, Делаем вывод, что подынтегральное выражение действительно представляет собой полный дифференциал некоторой функцииU(x; y).

Восстановим функцию U(x; y). Для этого пройдем несколько этапов:

а) проинтегрируем по переменной x функцию P(x; y), считая y постоянной величиной:

где представляет собой константу по отношению к переменной x и зависит только от y;

б) продифференцируем полученное выражение по переменной y, считая x константой, и приравняем его к функции Q(x; y):

в) из последнего соотношения найдем и затем после интег­рирования –

г) подставив в выражение из пункта а), получим искомую функцию U(x; y):

Займемся непосредственным вычислением исходного интеграла:

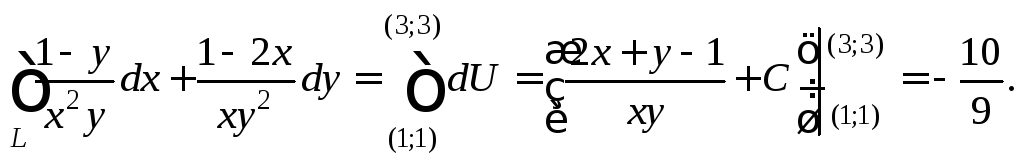
Задания