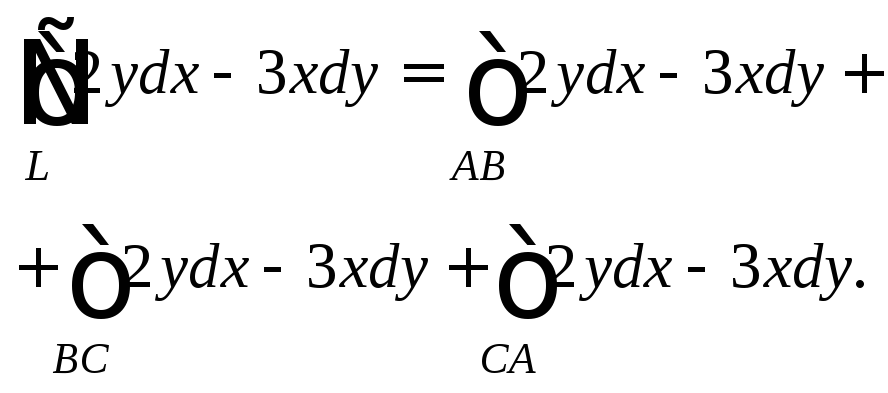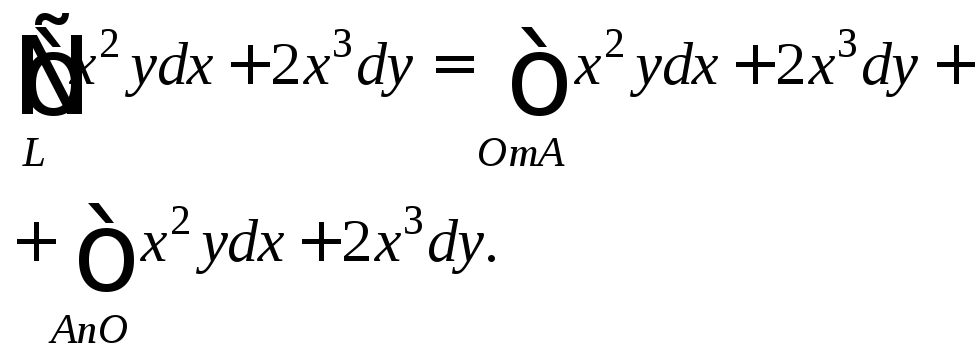I уровень

1.1. Вычислите криволинейный интеграл 1-го рода в случае явного задания кривой интегрирования:

1) где от точки A(2; 8) до точки B(1; 1);

2)  где L – отрезок прямой от точки O(0; 0) до точки C(1; 3);

3)  где от точки A(1; 2) до точки B(0; 1);

4)  где от точки O(0; 0) до точки B(1; 1);

5)  где L – контур с вершинами в точках A(2; 0), B(0; 4), O(0; 0);

6)  где L – прямоугольник с вершинами в точках A(3; 0), B(3; 5), C(0; 5), O(0; 0);

7)  где L – отрезок прямой от точки B(0; – 1) до точки C(1; 0).

1.2. Вычислите криволинейный интеграл 1-го рода где перейдя к параметрическому заданию кривой интегрирования.

II уровень

2.1. Вычислите криволинейный интеграл 1-го рода в случае явного задания кривой интегрирования:

1)  где от точки O(0; 0) до точки C(1; 1);

2)  где от точки A(– 1; 1) до точки B(3; 9);

3)  где от точки до точки

4)  где от точки O(0; 0) до точки

5)  где от точки A(e; 1) до точки

6)  где L – дуга параболы отсеченная параболой

7)  где L – отрезок прямой от точки O(0; 0) до точки C(1; 4).

2.2. Вычислите криволинейный интеграл 1-го рода в случае параметрического задания кривой интегрирования:

1)  где L – первая арка циклоиды

2)  где L – первая арка циклоиды

3)  где L – первый виток винтовой линии

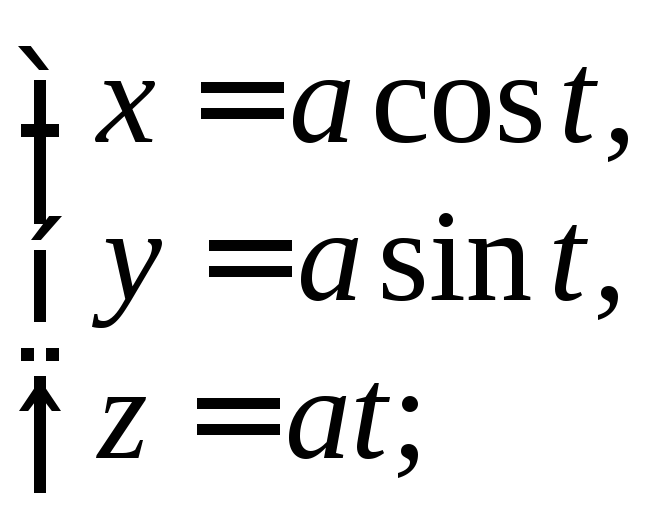
4)  где L – контур прямоугольника с вершинами в точках O(0; 0; 0), A(0; 2; 0), B(0; 2; 4), C(0; 0; 4);

5)  где L – виток конической винтовой линии

2.3. Вычислите криволинейный интеграл 1-го рода в случае задания кривой интегрирования в полярных координатах:

1)  где L – дуга кривой где

2)  где L – дуга кардиоиды

3)  где L – часть гиперболической спирали отдо

III уровень

3.1. Вычислите криволинейный интеграл 1-го рода где L – отрезок прямой от точки B(0; 2) до точки C(– 4; 0).

3.2. Вычислите криволинейный интеграл 1-го рода в случае параметрического задания кривой интегрирования:

1)  где L – окружность

2)  где L – полуокружность

3)  где L: 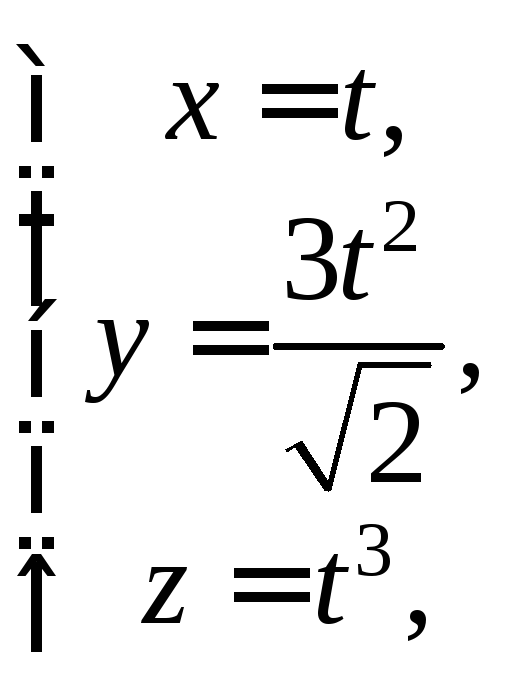причем

4)  где L – окружность

5)  где L – первая четверть эллипса

6)  где L – дуга астроиды заключенная между точками A(0; – 1) и B(1; 0).

26.2. Понятие криволинейного интеграла 2-го рода,

его свойства и вычисление. Формула Грина

Пусть на плоскости xOy задана гладкая незамкнутая кривая L, и на этой кривой определена вектор-функция

где P(x; y) и Q(x; y) – непрерывные функции.

Разобьем указанную кривую L произвольным образом на элементарные дуги На каждой из элементарных дугвыберем произвольную точку

Составим произведение значения функциина длину проекции дуги на ось Ox и произведение значения функции на длину проекции дуги на ось Oy. Запишем предельную сумму:

Обозначим через а черезУстремим так, чтобы иЕсли существует предел интегральных сумм, который не зависит ни от способа разбиения кривойL на части, ни от выбора точек то этотпредел называется криволинейным интегралом 2-го рода от функции по координатамx и y:

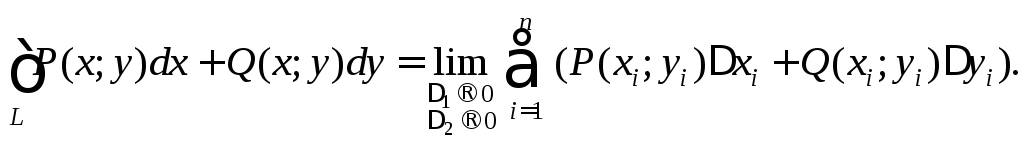
Если L – гладкая кривая в трехмерном пространстве, а – вектор-функция, заданная наL, причем P(x; y; z), Q(x; y; z) и R(x; y; z) – непрерывные функции в точках этой кривой, то в случае существования предела и при аналогичных плоской кривой условиях криволинейный интеграл 2-го рода по координатам x, y и z определяется равенством:

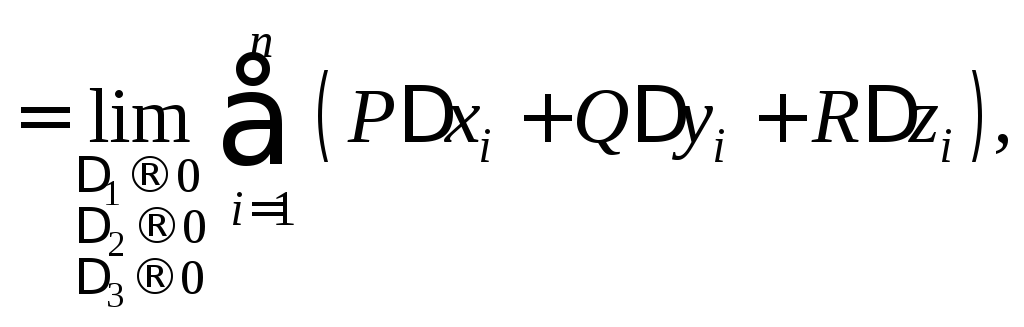
где в правой части формулы и

Если кривая L представляет собой замкнутый контур (т. е. начало кривой и ее конец совпадают), вводят понятие положительного и отрицательного направлений обхода контура. Положительным направлением обхода контура называется такое направление, при котором линия интегрирования обходится против хода часовой стрелки. Противоположное ему направление обхода контура называется отрицательным. При этом считают, что при положительном направлении обхода контураL.

Достаточное условие интегрируемости функции: если оп­ределенная в точках гладкой кривой вектор-функция имеет непрерывные координатные функцииP(x; y; z), Q(x; y; z) и R(x; y; z), то эта вектор-функция интегрируема по этой кривой.

Свойства криволинейного интеграла 2-го рода аналогичны свойствам криволинейного интеграла 1-го рода, кроме одного: величина криволинейного интеграла 2-го рода численно зависит от направления интегрирования, т. е.

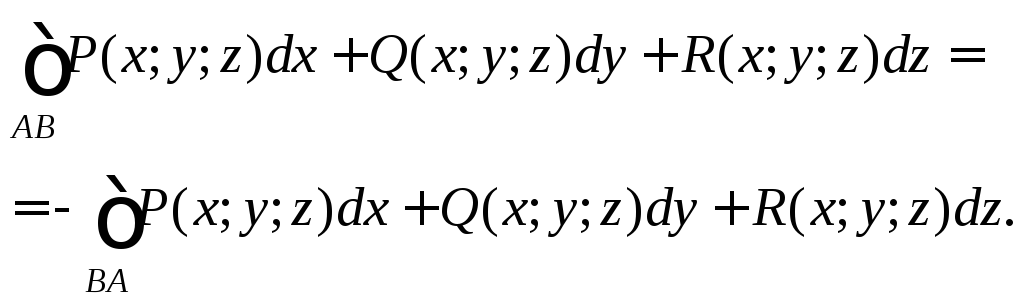
Допустим, что координатные функции P(x; y; z), Q(x; y; z) и R(x; y; z) непрерывны на рассматриваемой кривой. Вычисление криволинейного интеграла 2-го рода сводится к вычислению определенных интегралов. Вид формулы зависит от способа задания кривой. Возможны следующие случаи:

1. Если плоская кривая L с началом в точке A и концом в точке B задана явно уравнением причем при изменении x от a до b кривая L описывается от A к B, то

(26.6)

2. Если плоская кривая L с началом в точке A и концом в точке B задана явно уравнением причем при измененииy от c до d кривая L описывается от A к B, то

(26.7)

3. Если плоская кривая L с началом в точке A и концом в точке B задана параметрически с помощью формул где причем при изменении параметра t от ккриваяL описывается от A к B, функции и непрерывно дифференцируемы, тогда

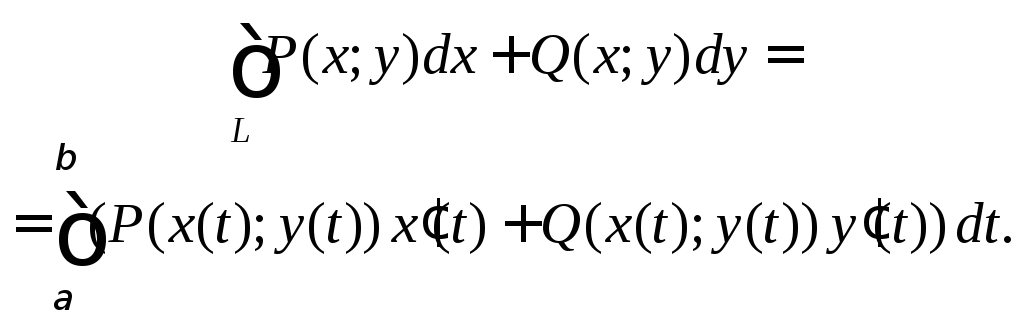(26.8)

4. Если пространственная кривая L задана параметрически с помощью формул где причем при изменении параметра t от ккривая описывается отA к B, то

(26.9)

причем в правой части формулы – и

Формула Грина: если функции P(x; y) и Q(x; y) непрерывно дифференцируемы в замкнутой ограниченной области D, то имеет место формула Грина:

(26.10)

где L – граница области D, интегрирование вдоль которой производится в положительном направлении (рис. 26.2).

Рис. 26.2

Пример 1. Вычислить криволинейный интеграл 2-го рода по указанной дуге кривой L:

1) гдеL – дуга параболы от точкиO(0; 0) до точки A(1; 1);

2) гдеL – четверть эллипса

3) гдеL – отрезок прямой, соединяющий точки A(1; 2; 3) и B(3; 5; 7).

Решение. 1) Вычислим заданный интеграл по формуле (26.6):

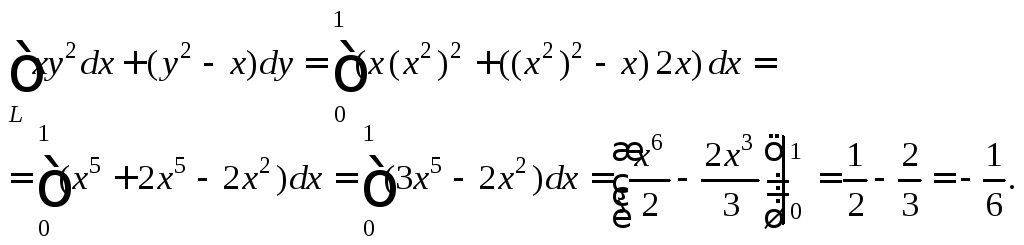
2) Вычислим заданный интеграл по формуле (26.8):

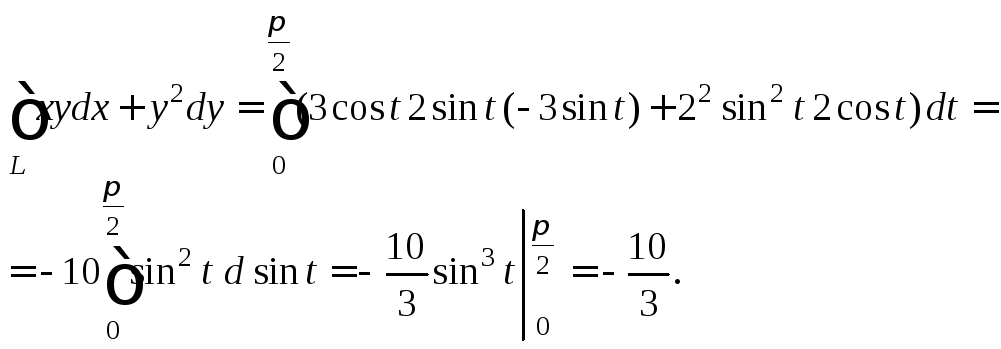
3) Запишем параметрические уравнения данной прямой:

где

Воспользовавшись формулой (26.9), вычислим интеграл:

Пример 2. Вычислить криволинейный интеграл 2-го рода по указанному замкнутому контуру L:

1) гдеL – контур с вершинами в точкахA(1; 0), B(3; 1) и C(0; 5);

2) гдеL – контур, образованный дугами парабол при положительном обходе контура интегрирования.

Решение. 1) Нарисуем (рис. 26.3).

Рис. 26.3

Представим данный интеграл как сумму трех интегралов по отрезкам прямых: Вычислим интеграл по каждому из отрезков интегрирования.

Отрезок АВ: уравнение где поэтому

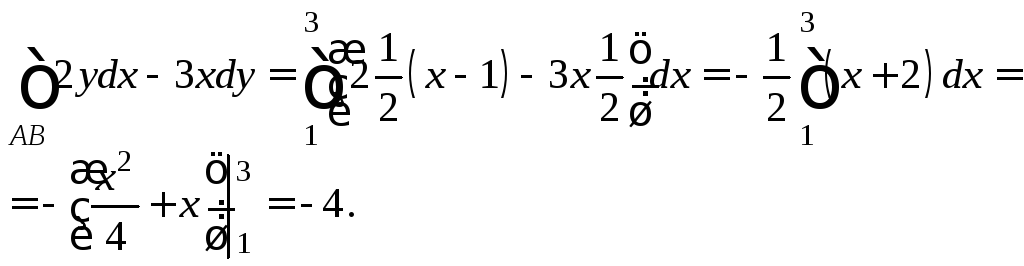
Отрезок ВС: уравнениегдеx меняется от 3 до 0, поэтому

Отрезок СА: уравнение гдепоэтому

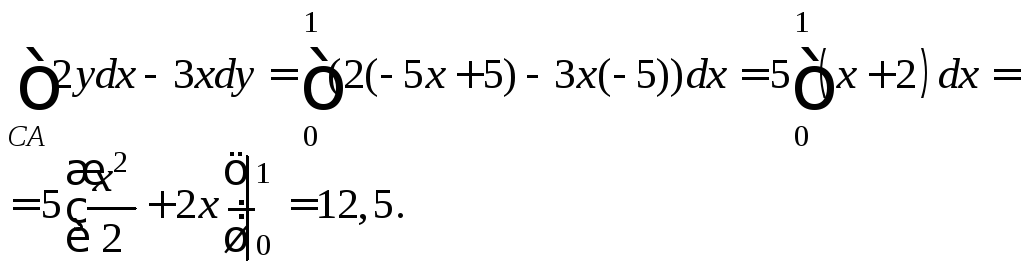
Чтобы получить искомый результат, просуммируем промежуточные данные:

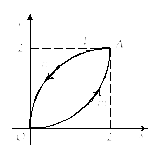
2) Нарисуем контур L (рис. 26.4).

Рис. 26.4

Представим данный интеграл как сумму двух интегралов по дугам различных парабол: По каждой из кривых интегрирования вычислим интеграл отдельно.

Дуга OmA: уравнение гдепоэтому

Дуга AnO: уравнение гдеx меняется от 2 до 0, поэтому

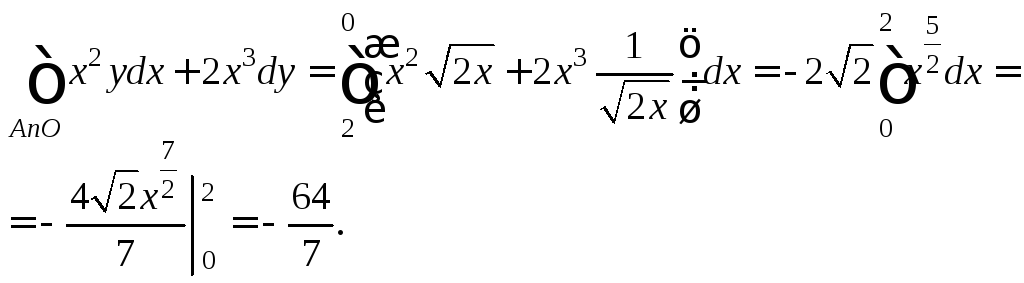
Чтобы получить искомый результат, просуммируем промежуточные данные:

Задания