I уровень

1.1. Вычислите криволинейный интеграл 2-го рода по указанной дуге кривой L:

1)  где L – дуга параболы от точки A(– 1; 2) до точки B(1; 2);

2)  где L – дуга параболы от точки O(0; 0) до точки A(2; 8);

3)  где L – дуга кривой от точки B(– 1; – 1) до точки C(1; 1);

4)  где L – дуга пространственной кривой соединяющая точки O(0; 0; 0) и A(1; 1; 1);

5)  где L – отрезок прямой от точки A(1; 1) до точки B(4; 3);

6)  где L – дуга окружности

II уровень

2.1. Вычислите криволинейный интеграл 2-го рода по указанной дуге кривой L:

1)  где L – дуга от точки O(0; 0) до точки A(2; 4):

а) прямой у = х,б) параболы у = х²,

в) кривой г) кубической параболы

2)  где L – дуга кривой от точки A(1; 0) до точки В(е²; 2);

3)  где L – дуга кривой от точки O(0; 0) до точки C(3; 1);

4)  где L – отрезок прямой от точки A(1; 1) до точки B(4; 3);

5)  где L – окружность

6)  где L – дуга окружности

7)  где L – окружность

8)  где L – дуга винтовой линии

III уровень

3.1. Вычислите криволинейный интеграл 2-го рода по указанной дуге кривой L:

1)  где L – дуга кривой от точки A(–3; 3) до точки B(1; 1);

2)  где L – окружность в пересечении сферы и конуса при

3)  где L – дуга кривой

4)  где L – арка циклоиды

26.3. Геометрические и физические приложения

криволинейных интегралов

1. Если L – гладкая кривая с началом в точке A и концом в точке B, то

(26.11)

где l – длина дуги кривой L от точки A до точки B.

2. Если f(x; y) – непрерывная функция, выражающая линейную плотность распределения массы m по гладкой кривой L, то криволинейный интеграл 1-го рода представляет собой массу данной материальной кривой:

(26.12)

В этом состоит физический смысл криволинейного интеграла 1-го рода.

3. Для нахождения координат центра масс дуги кривой L пользуются следующими формулами:

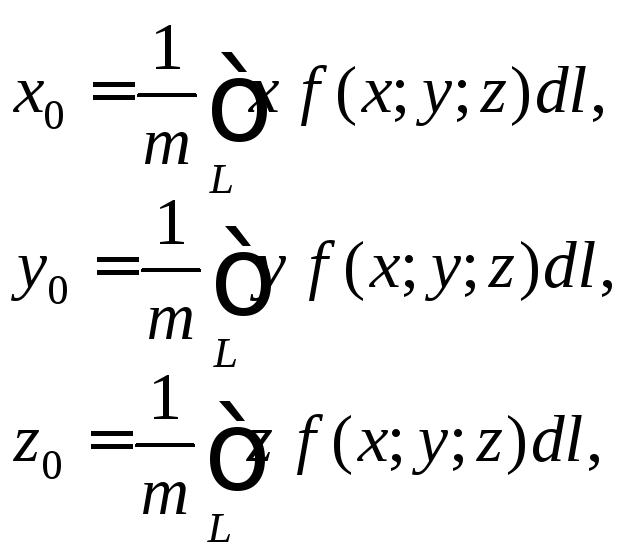(26.13)

где m – масса материальной кривой L с линейной плотностью f(x; y), которая вычисляется по формуле (26.12).

4. Если – переменная сила, которая действует вдоль контураL, то криволинейный интеграл 2-го рода выражает работуA этой силы т. е.

(26.14)

5. Площадь S области D, ограниченной простым замкнутым контуром L, вычисляется по формуле:

(26.15)

причем обход контура интегрирования L совершается в положительном направлении.

Пример 1. Найти длину дуги кривой, заданной указанными соотношениями:

1)  (винтовая линия);

2)

Решение. 1) Найдем производные функций и Применив формулуопределим дифференциал длины дуги в случае параметрического задания кривой:

По формуле (26.11) вычислим длину дуги кривой:

2) Найдем производные функций и возведем их в квадрат:

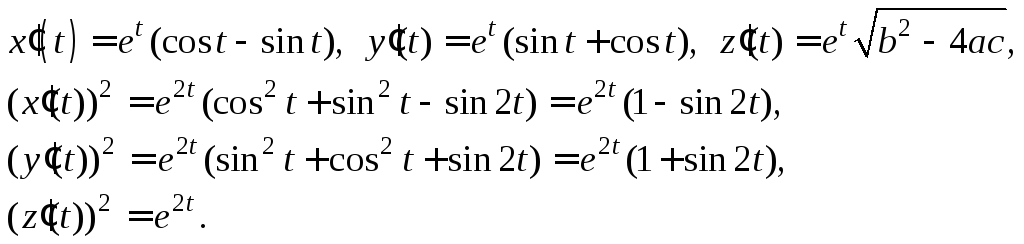
С помощью формулы определим дифференциал длины дуги в случае параметрического задания кривой:Вычислим длину дуги, воспользовавшись формулой (26.11):

Пример 2. Найти массу дуги указанной кривой:

1)  от точки O(0; 0) до точки A(4; 8) с плотностью распределения массы

2) винтовой линии с плотностью распределения массы

Решение. 1) Найдем производную функции и возведем ее в квадрат: Воспользовавшись формулойопределим дифференциал длины дуги кривой:гдеВычислим массу дуги по формуле (26.12):

2) Найдем производные функций и

Определим дифференциал длины дуги в случае параметрического задания кривой:

Вычислим массу дуги, воспользовавшись формулой (26.12):

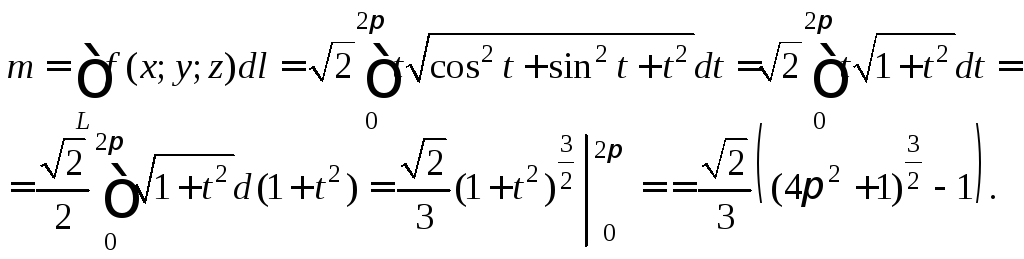
Пример 3. Найти центр масс однородной дуги циклоиды, заданной уравнениями

Решение. Найдем производные функций

Определим дифференциал длины дуги в случае параметрического задания кривой:

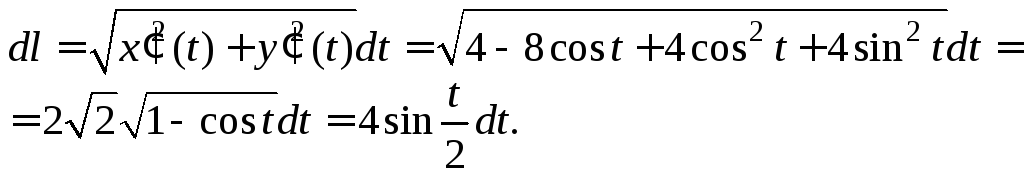
Вычислим массу дуги, воспользовавшись формулой (26.12):

Найдем абсциссу центра масс данной дуги кривой, применив одну из формул (26.13):

После интегрирования по частям имеем:

Найдем ординату центра масс данной дуги кривой, применив одну из формул (26.13):

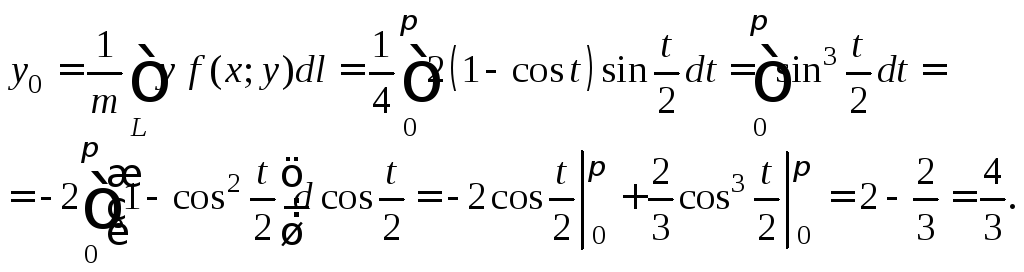
Приходим к ответу: центр масс имеет координаты

Пример 4. Найти работу переменной силы при перемещении материальной точки единичной массы вдоль отрезкаAB, где A(1; 1; 1), B(2; 4; 8).

Решение. Предварительно запишем параметрические уравнения прямой AB. Направляющим вектором этой прямой является вектор прямая проходит через точкуA(1; 1; 1), поэтому параметрическими уравнениями прямой будут соотношения: где при изменении переменнойx от 1 до 2 параметр t заключен между 0 и 1, т. е.

Применив формулу (26.14) и подставив соответствующие выражения для функций P(x; y; z), Q(x; y; z) и R(x; y; z), получим При вычислении данного интеграла необходимо перейти к определенному интегралу, для чего следует применить формулу (26.9) и учесть, чтоПолучим

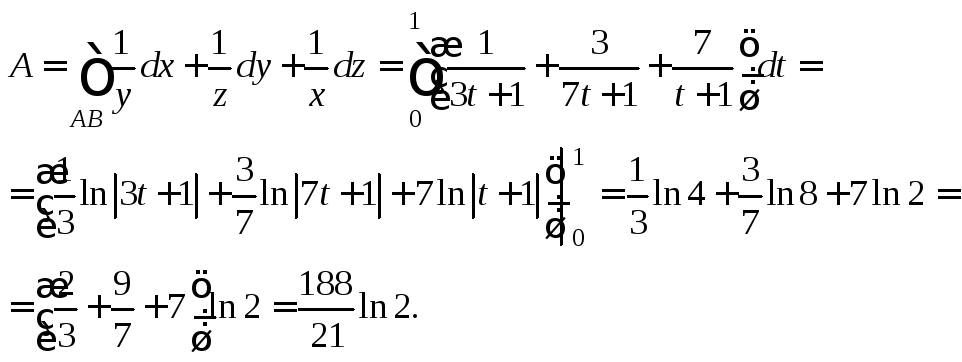
Пример 5. С помощью криволинейного интеграла найти площадь области D, ограниченной указанным замкнутым контуром L:

1) – окружность;

2) – астроида.

Решение. 1) Запишем параметрические уравнения окружности:

Воспользуемся формулой (26.15):

2) Воспользуемся формулой (26.15):

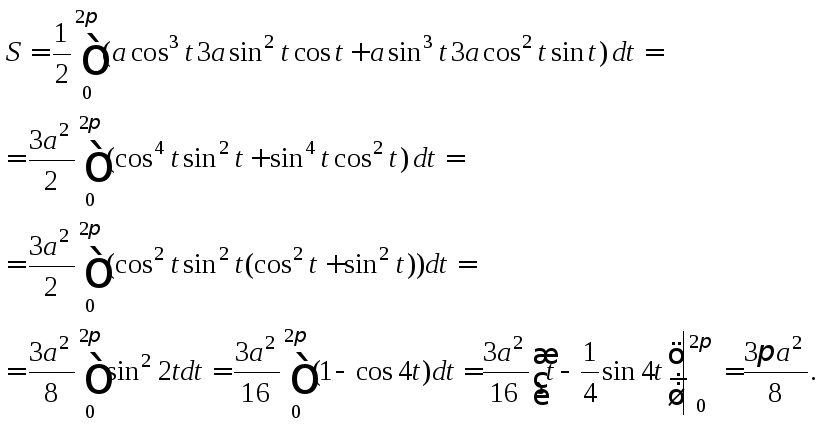
Задания