26. Криволинейные интегралы

26.1. Понятие криволинейного интеграла 1-го рода,

его свойства и вычисление

Пусть на плоскости xOy задана гладкая незамкнутая кривая L с началом в точке A и концом в точке B, не имеющая самопересечений. Допустим, что на этой кривой определена непрерывная функция Разобьем указанную кривую L произвольным образом на элементарные дуги длины которых будем считать соответственно равнымиНа каждой из элементарных дугвыберем произвольную точкуОбозначим черези составиминтегральную сумму

Устремим так, чтобыЕсли существует предел интегральных сумм, который не зависит ни от способа разбиения кривойL на части, ни от выбора точек то этот предел называетсякриволинейным интегралом 1-го рода от функции f(x; y) вдоль кривой L:

dl называют дифференциалом длины дуги, а саму кривую L – линией интегрирования. При этом говорят, что функция f(x; y) интегрируема по кривой L.

Если L – гладкая кривая в трехмерном пространстве без самопересечений, а f(x; y; z) – непрерывная функция в точках этой кривой, то криволинейный интеграл 1-го рода по этой кривой определяется равенством

в случае существования предела и при аналогичных плоской кривой условиях.

Если кривая L представляет собой замкнутый контур (т. е. начало кривой и ее конец совпадают), используют специальное обозначение:

Достаточное условие интегрируемости функции: если функция определена и непрерывна в точках гладкой, не имеющей самопересечений, кривой, то она интегрируема по этой кривой.

Если функции f(x; y), f₁(x; y) и f₂(x; y) интегрируемы по гладкой кривой L, то справедливы следующие свойства:

1) линейность:

где

2) аддитивность: если гладкая или кусочно-гладкая кривая L состоит из конечного числа гладких дуг то

3) независимость от направления пути интегрирования: если кривая L соединяет точки A и B, то

4) оценка модуля интеграла:

Допустим, что – функция, непрерывная в точках кривойL. Вычисление криволинейного интеграла 1-го рода сводится к вычислению определенного интеграла, причем вид формулы зависит от способа задания кривой L:

1. Если кривая L задана явно уравнением то

(26.1)

2. Если кривая L задана явно уравнением то

(26.2)

3. Если плоская кривая L задана параметрически формулами гдето

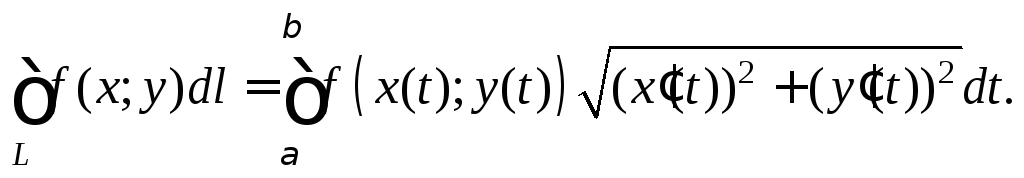(26.3)

4. Если пространственная кривая L задана параметрически формулами гдеа– непрерывная в точках этой кривой функция, то

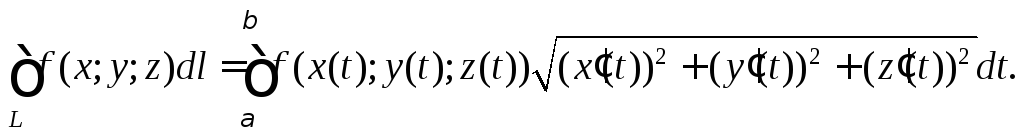(26.4)

5. Если кривая L задана уравнением в полярных координатах гдето

(26.5)

Пример 1. Вычислить криволинейный интеграл 1-го рода в случае явного задания кривой интегрирования:

1) гдеот точкиA(1; 2) до точки B(4; 4);

2)  где от точкиA(0; 2) до точки B(– 1; 0);

3)  где L – контур треугольника AOB с вершинами в точках A(2; 0), O(0; 0), B(0; 2).

Решение. 1) В уравнении кривой L выразим x через y: гдеДля этого вычислим производную функциипо переменнойy: Далее для нахождения элемента длины дуги кривойL целесообразно применить формулу так как кривая задана явно уравнением(см. формулу (26.2)):

.

Вычислим исходный криволинейный интеграл, применив формулу (26.2):

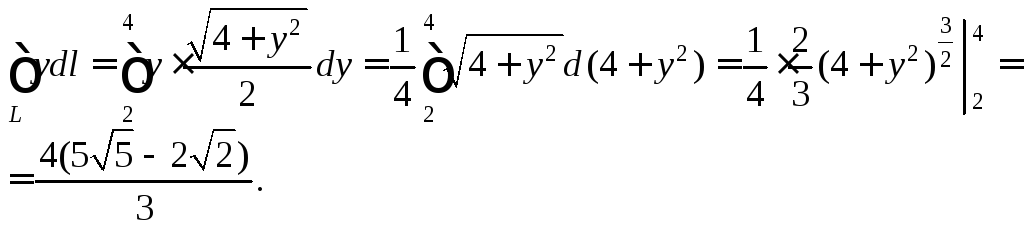
2) В уравнении кривой L переменная y выражена через x: где x меняется от 0 до –1. Вначале вычислим производную функции по переменнойx: Затем с учетом случая 1 применим формулуи найдем элемент длины дуги кривойL: Вычислив исходный криволинейный интеграл, применив формулу (26.1), получим:

3) Изобразим треугольник AOB (рис. 26.1).

Рис. 26.1

Разобьем контур интегрирования на три части: Рассмотрим отдельно каждый из отрезков интегрирования. Отрезок ОА: уравнение соответствующей прямой получаем элемент длины

дуги где

Отрезок АВ: уравнение прямой интегрирования отсюда элемент длины дуги этой прямойгде

Отрезок ОВ: уравнение прямой получаем элемент длины дугигде

Вычислим отдельно каждый из интегралов суммы:

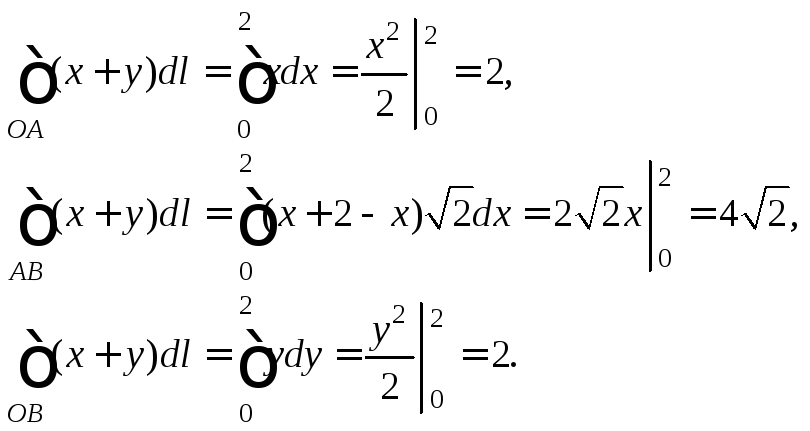
Тогда исходный интеграл будет равен

Пример 2. Вычислить криволинейный интеграл 1-го рода, используя параметрическое задание кривой интегрирования:

1) гдеL – нижняя полуокружность

2) гдеL – первый виток винтовой линии

3) гдеL – отрезок прямой, соединяющий точки A(1; 3; 5) и B(4; 7; 5).

Решение. 1) Перейдем к параметрическому заданию данной окружности: причемДля того чтобы воспользоваться формулой (26.3), найдем элемент длины дуги:

Вычислим криволинейный интеграл, перейдя к определенному интегралу по указанной формуле:

2) Поскольку задан первый виток винтовой линии, то Вычислим криволинейный интеграл, перейдя к определенному интегралу по формуле (26.4). Вначале найдем элемент длины дуги:

Тогда

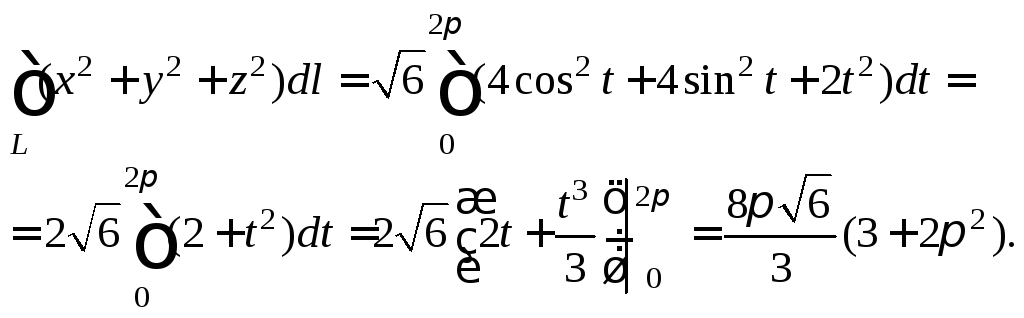
3) Запишем уравнение данной прямой, проходящей через точку A(1; 3; 5), направляющий вектор которой

Перейдем к параметрическому заданию этой прямой: причемтак какВычислим криволинейный интеграл, перейдя к определенному интегралу по формуле (26.3), найдя вначале элемент длины дуги: Получим:

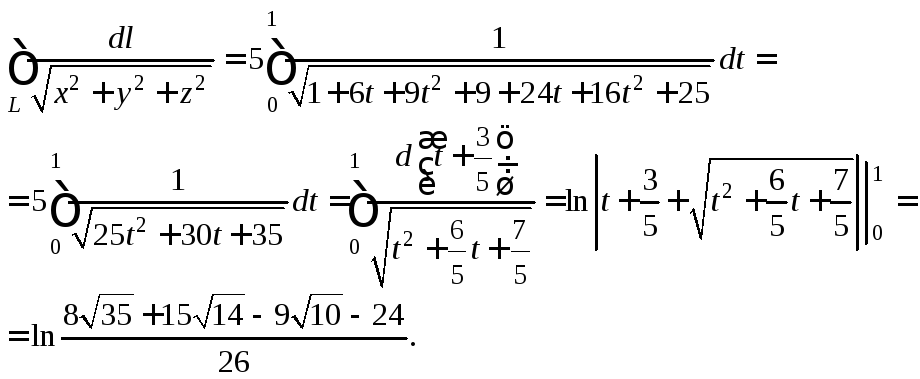
Пример 3. Вычислить криволинейный интеграл 1-го рода в случае задания кривой интегрирования полярным уравнением:

1) где L – лепесток лемнискаты

2)  где L – дуга кардиоиды

Решение. 1) В данном случае необходимо использовать формулу (26.5). Но вначале найдем производную функции и возведем ее в квадрат:Применив формулувыясним, каков в нашем случае элемент длины дуги:

Вычислим исходный криволинейный интеграл, перейдя к определенному интегралу и воспользовавшись формулами перехода от декартовых координат к полярным ис учетом того, чтоИмеем

2) Воспользуемся формулой (26.5). Найдем производную заданной функции и возведем ее в квадрат:

Выясним, каков элемент длины дуги. Так как то

Вычислим исходный криволинейный интеграл, перейдя к определенному интегралу:

Задания