I уровень

1.1. Найдите матрицу C оператора в некотором базисе если известны матрицы операторовA и B в этом базисе и взаимосвязь операторов A, B, C:

1)

2)

3)

1.2. Составьте матрицу C оператора, переводящего базисные векторы пространствав векторыа также формулы, по которым может быть найден векторпространства

1.3. Вектор в базисепространстваимеет координаты (2; 3). Найдите координаты вектора в базисегде

1.4. В базисе пространстваоператорA имеет матрицу Найдите матрицуB этого же оператора в базисе

II уровень

2.1. Выясните, является ли линейным оператором пространства преобразованиеA, переводящее любой вектор в вектор:

1) 2)

3) 4)

2.2. Найдите матрицу линейного оператора, переводящего в пространстве векторыв векторысоответственно:

1)

2)

3)

2.3. Известна матрица A линейного оператора в стандартном базисе пространства Найдите матрицу этого же оператора в новом базисепространства

1)

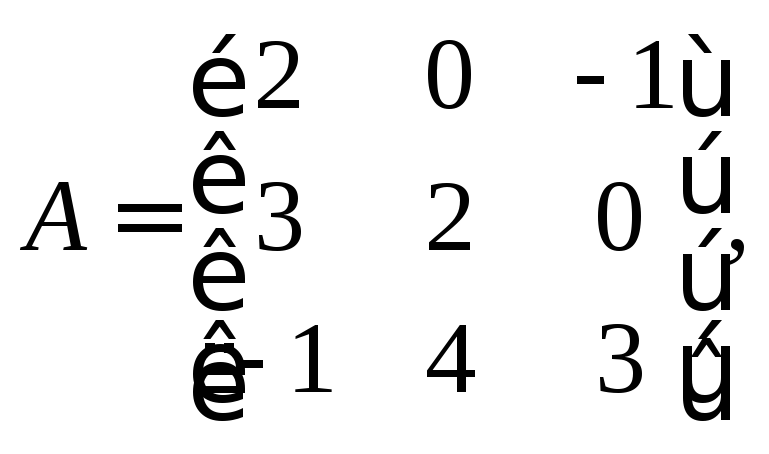
2)

III уровень

3.1. Докажите, что оператор дифференцирования D является линейным преобразованием пространства всех многочленов степени не выше n от одной переменной с действительными коэффициентами. Найдите матрицу оператора D в базисе

3.2. Докажите, что поворот координатной плоскости xOy на угол вокруг начала координат есть линейное преобразованиеЗапишите матрицу этого оператора в базисепространства

3.3. Линейное преобразование A в базисе имеет матрицу

Найдите матрицу преобразования в базисе

3.4. Найдите матрицу линейного преобразования A в ортонормированном базисе пространствагде

23.4. Собственные векторы и собственные значения

линейного оператора

Число называетсясобственным значением оператора A, если существует ненулевой вектор такой, что

(23.15)

Вектор x, удовлетворяющий условию (23.15), называется собственным вектором оператора A, соответствующим собственному значению . Множество всех собственных значений оператора A называется его спектром.

Пусть – базис линейного пространстваA – матрица оператора A в этом базисе, – собственный вектор оператораA, X – столбец координат вектора x. Тогда условие (23.15) в матричной форме принимает вид илигдеE – единичная матрица, O – нулевая матрица. Матричное уравнение представляет собой однородную систему уравнений:

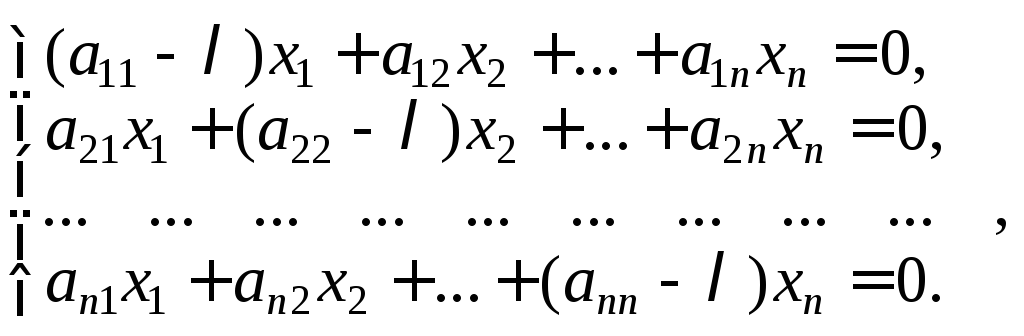(23.16)

Система уравнений (23.16) имеет отличное от нуля решение тогда и только тогда, когда:

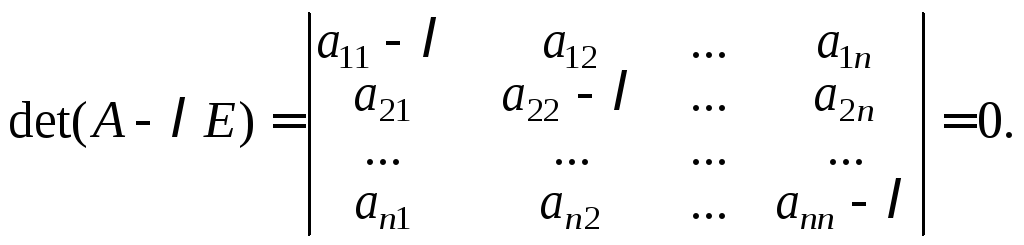(23.17)

Уравнение n-й степени (23.17) относительно переменной  называется характеристическим уравнением линейного оператора А (матрицы А). Корни этого уравнения и являются собственными значениями оператора А.

Пусть из уравнения (23.17) найден корень Чтобы найти собственные векторы оператораА, соответствующие этому собственному значению, нужно подставить в (23.16) и, решив полученную однородную систему линейных уравнений, найти координаты искомых собственных векторов.

Пример 1. Найти собственные значения и собственные векторы оператора А, заданного в некотором базисе пространстваматрицей

Решение. Составляем характеристическое уравнение (23.17) для заданной матрицы

Вычисляя определитель, имеем уравнение:

т. е.

Находим и

Получили собственные значения:

Найдем собственные векторы, соответствующие этим собственным значениям. Запишем систему уранений (23.16) для данного случая:

(23.18)

Подставив в (23.18), получим систему:

Решение системы:

Получили множество собственных векторов, соответствующих собственному значению

Подставив в (23.18), получим однородную систему уравнений:

решив которую, имеем Тогда множество собственных векторов, соответствующих собственному значениюбудет

Пример 2. Найти собственные значения и собственные векторы оператора А, заданного в некотором базисе пространства матрицей

Решение. Составляем характеристическое уравнение (23.17) для заданной матрицы:

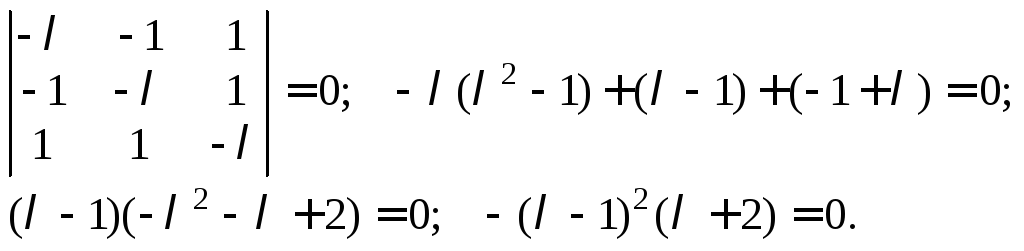
Получаем собственные значения:

Найдем собственные векторы, соответствующие этим собственным значениям. Запишем соответствующую систему уравнений

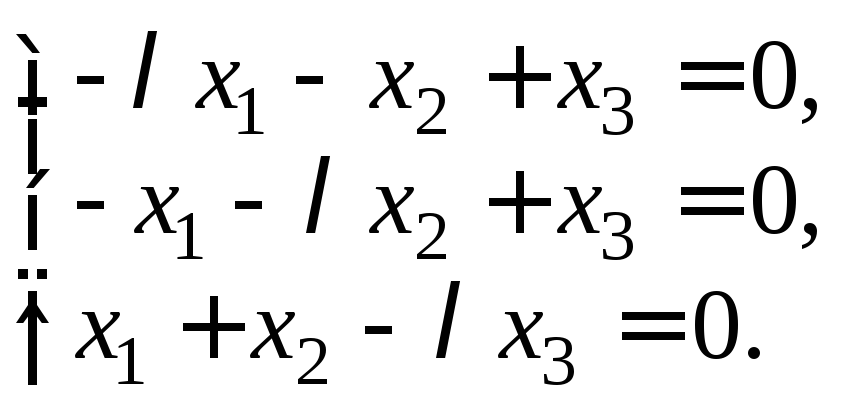(23.19)

Подставляя в систему уравнений (23.19), получим однородную систему линейных уравнений:

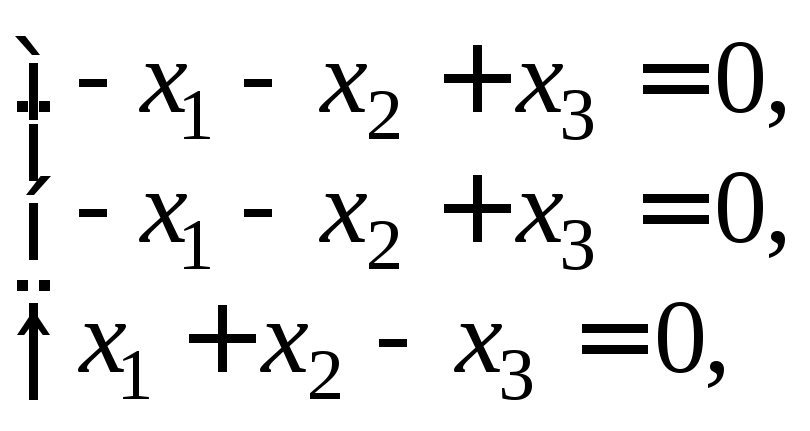
решение которой

Получаем множество собственных векторов, соответствующих собственному значению

Подставляя в систему уравнений (23.19), получаем однородную систему линейных уравнений:

Ее решением будет

Получили множество собственных векторов, соответствующих собственному значению

Задания