I уровень

1.1. Найдите единичный вектор, сонаправленный с данным вектором =(4; 0;-3)

1.2. Даны векторы =(1; 2; 1;) иНайдите угол между векторамии

1.3. Нормируйте вектор =(3; 1; 2; 1).

1.4. Определите скалярное произведение векторов и

II уровень

2.1. Определите угол между векторами и

1) 2)

2.2.Найдите векторы, дополняющие до ортонормированного базиса следующие системы векторов:

1)

2)

III уровень

3.1. Выясните, ортогонален ли вектор

1) 2)

подпространству решений системы уравнений

3.2. Найдите длины диагоналей n-мерного куба со стороной, равной 1, где n-мерный куб определить по аналогии с двумерным (квадратом) и обычным трехмерным кубом.

23.3. Линейные операторы. Матрица

линейного оператора

Пусть V и – линейные пространства.Оператором А, действующим из V в называетсяотображение сопоставляющее каждому элементуединственный элементобозначаемыйилиВекторy называется образом вектора x.

Оператор называетсялинейным, если для любых векторов изV и любого числа имеем:

Если то операторA называется функцией (числовой).

Если V – произвольное линейное пространство и то операторA называется функционалом.

Если то линейный операторA называется линейным преобразованием пространства V.

Пусть – множество всех линейных операторов, действующих изV в иСуммой операторов A и B называется оператор, обозначаемый который определяется условием

Произведением оператора A на число называется оператор, обозначаемыйкоторый определяется условием

Нулевым линейным оператором называется оператор O такой, что Тождественным оператором называется линейный оператор I такой, что для него выполняется

Теорема. Относительно введенных операций сложения линейных операторов и умножения линейного оператора на число множество само образует линейное пространство.

Произведением линейных преобразований A и B называется линейное преобразование, обозначаемое которое определяется условиемНатуральная степень оператора определяется равенством

Справедливы следующие свойства:

1)

2)

3)

4)

В общем случае

5)

Линейное преобразование B (обозначаемое ) называетсяобратным к линейному преобразованию A, если

Если для преобразования A из того, что всегда следует, чтото говорят, что операторA является взаимно-однозначным отображением V на

Теорема. Для того чтобы для линейного преобразования A существовало обратное линейное преобразование необходимо и достаточно, чтобы оператор был взаимно-однозначным отображениемV на

Пусть – базис линейного пространстваиA – линейный оператор из вТогда векторx разлагается по базису:

Если то

Если – образы базисных векторовто они также разлагаются по заданному базису:

(23.6)

Матрица

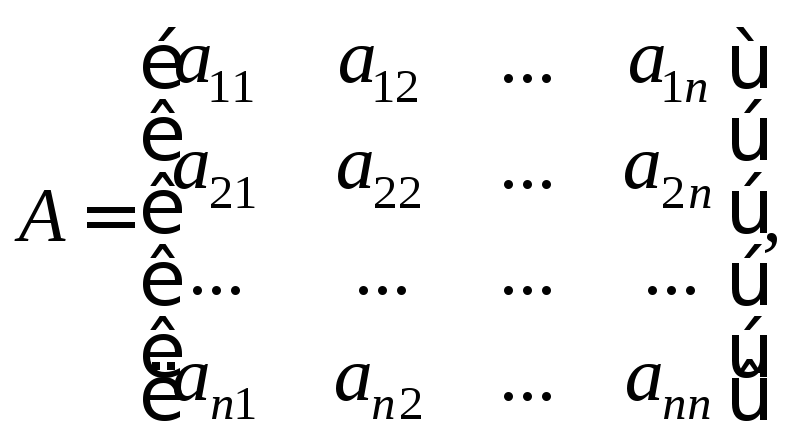(23.7)

у которой элементы столбцов являются соответственно координатами разложений (23.6), называется матрицей оператора A в базисе

Пусть для имеем разложение в базисе

(23.8)

Тогда для соответствующего образа существует разложение

(23.9)

В случае задания матрицы (23.7) оператора A, он определяется ею однозначно, а именно и его образавыполняется

где X и Y – столбцы координат (23.8) и (23.9) векторов x и y соответственно, т. е.

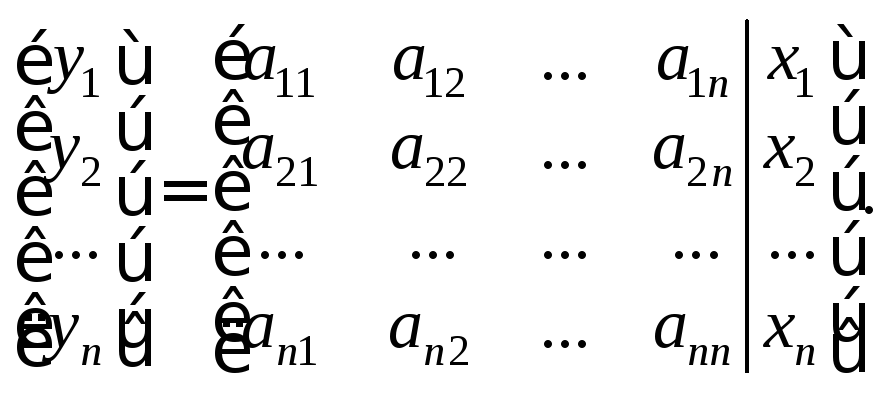(23.10)

Все операции над линейными операторами, которые рассматривались выше, распространяются на матричную форму задания линейного оператора как соответствующие операции над матрицами, т. е. в заданном базисе оператор имеет матрицуоператор– матрицуAB и т. д. При этом нулевой оператор O имеет нулевую матрицу, а тождественный оператор I – единичную матрицу.

Пусть в линейном пространстве заданы два произвольных базисаиТогда каждый вектор второго базиса разлагается по первому базису:

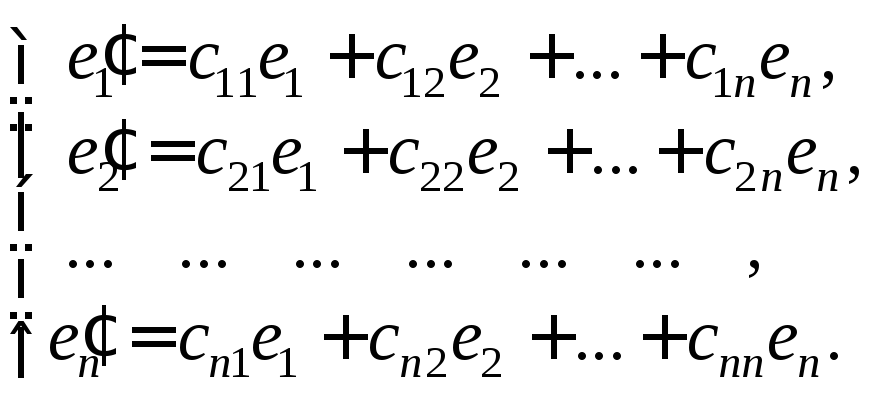(23.11)

Матрица

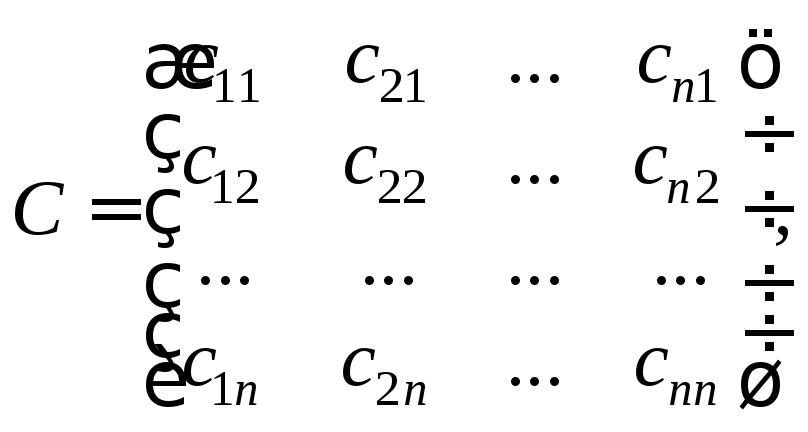(23.12)

транспонированная к матрице системы (23.11), называется матрицей перехода от базиса к базису

Связь между координатами одного и того же вектора x в базисах устанавливают формулы:

(23.13)

где X – матрица-столбец координат вектора x в базисе

 – матрица-столбец координат этого же вектора x в базисе

Формулы (23.11) и (23.12) выражают зависимость между координатами вектора x в базисах

Если A – линейный оператор, имеющий в базисах линейного пространстваматрицыA и B соответственно, то формула преобразования матрицы оператора при переходе к новому базису имеет вид:

(23.14)

Пример 1. Пусть – линейное пространство всех функций, непрерывных на отрезкеДля всехопределен операторJ по формуле

Доказать, что J – линейный оператор из в

Решение. Оператор является непрерывной функцией на отрезкеХорошо известно, что операция интегрирования обладает свойствами линейности, следовательноJ – линейный оператор из в

Пример 2. Пусть – линейное пространство всех действительных функций, определенных и дифференцируемых на отрезкеДляопределим операторD по формуле Очевидно, чтоD – линейный оператор из впоскольку линейность следует из свойств линейности производной.

Пример 3. Известно, что оператор A переводит базисные векторы линейного пространствав векторыВ базисе найти:

1. матрицу оператора A;

2. образ вектора

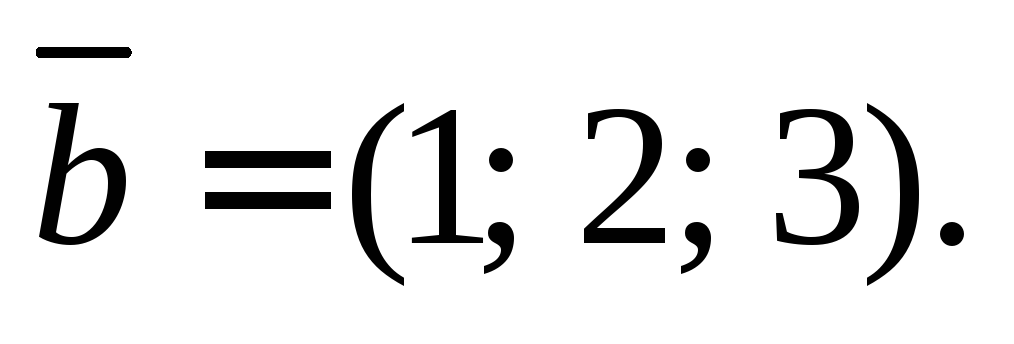
Решение. 1) По условию Поэтому первый столбец матрицыA оператора составляют координаты вектора Посколькуто второй столбец матрицыA и состоит из координат вектора Третий столбец искомой матрицы состоит из координат векторатак какСледовательно, матрицаA имеет вид:

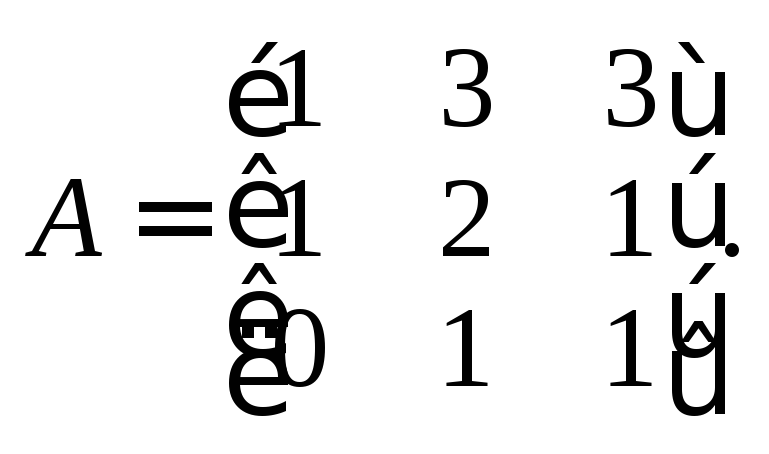
2) Пусть где– образ вектораТогда, согласно формуле (23.10), имеем:

Получаем

Пример 4. Известно, что операторы A и B переводят базисные векторы соответственно в векторы Записать формулы, по которым можно найти векторпространства

Решение. Пусть в базисе заданы векторыиЗапишем матрицы операторовв указанном базисе. Записывая координаты векторовстолбцами, получим матрицуА. Используя аналогично координаты векторов получим матрицуB:

Для того чтобы получить матрицу осуществим соотвествующие линейные операции над матрицамиA и B. Тогда

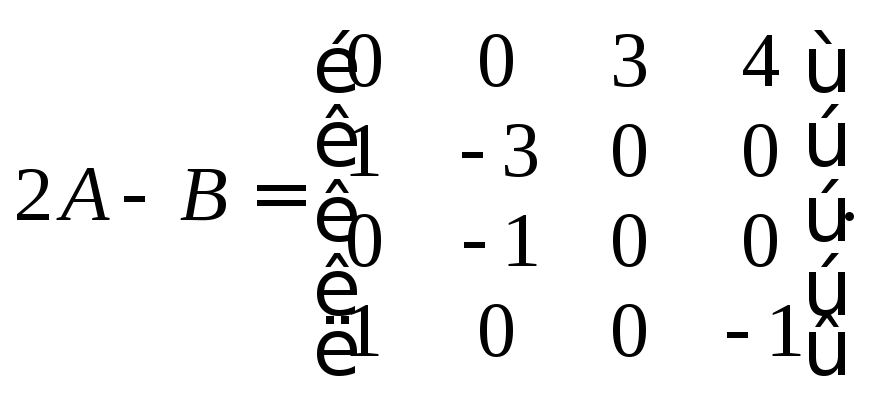
Если X, Y – матрицы-столбцы координат векторов x, y соответственно, то в матричной форме имеем:

Перемножая матрицы в правой части последнего равенства, получаем формулы для нахождения координат искомого вектора y:

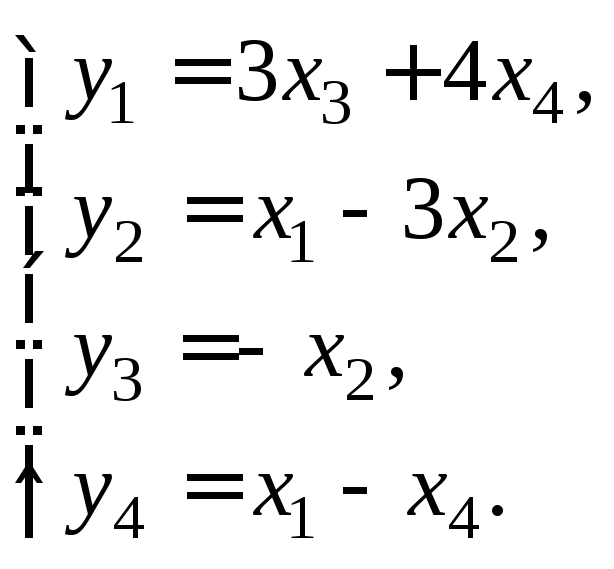
Пример 5. В базисе пространствавекторa имеет координаты (1; 2; 3). Найти координаты вектора a в базисе где

Решение. Имеем Следовательно, матрица перехода от базиса к базисув данном случае имеет вид:

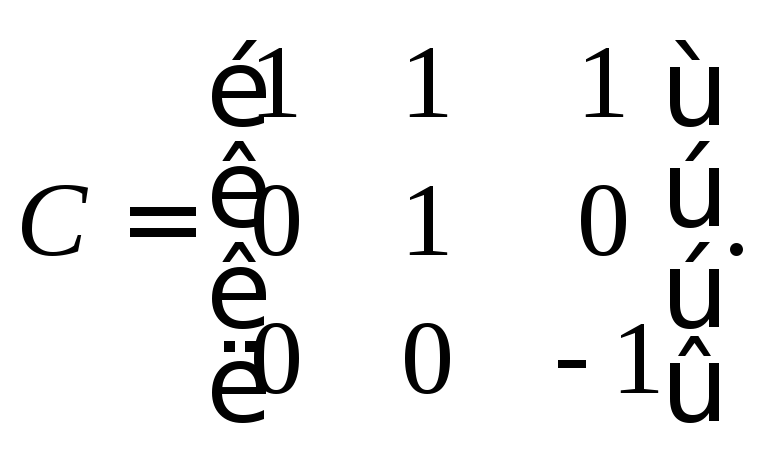
По условию и по формуле (23.13)Найдем матрицуВычисляем:

(как произведение элементов диагонали).

Находя алгебраическое дополнение для каждого элемента матрицы C, получаем матрицу

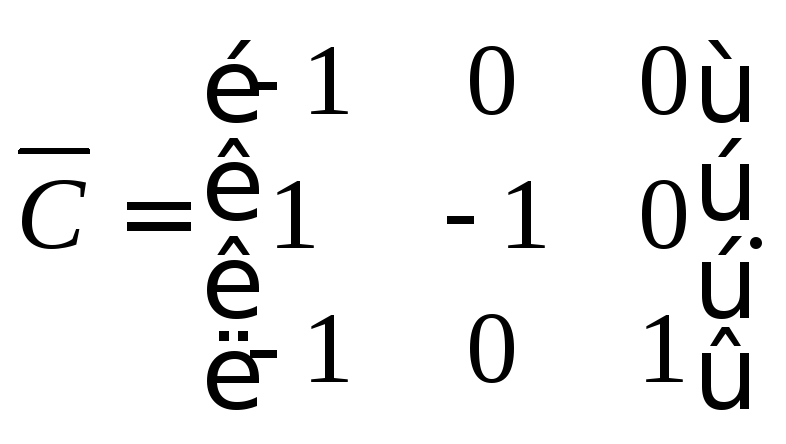
Согласно формуле нахождения обратной матрицы, имеем

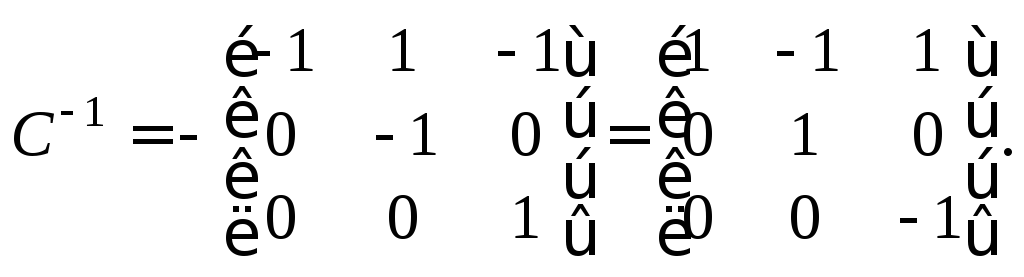
Тогда по формуле (23.13) получаем:

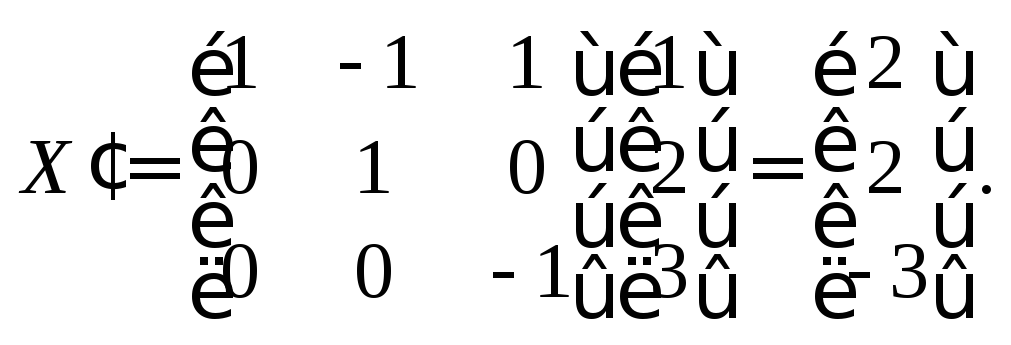
Таким образом, вектор a в базисе имеет координаты

Пример 6. В базисе пространстваоператорA имеет матрицу 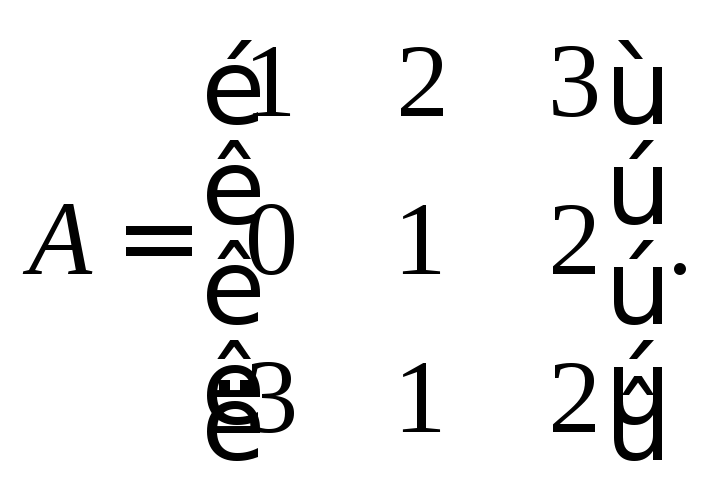Найти матрицуB этого же оператора в базисе где

Решение. Используя условие и равенства (23.11), (23.12), запишем матрицу перехода от базиса к базису

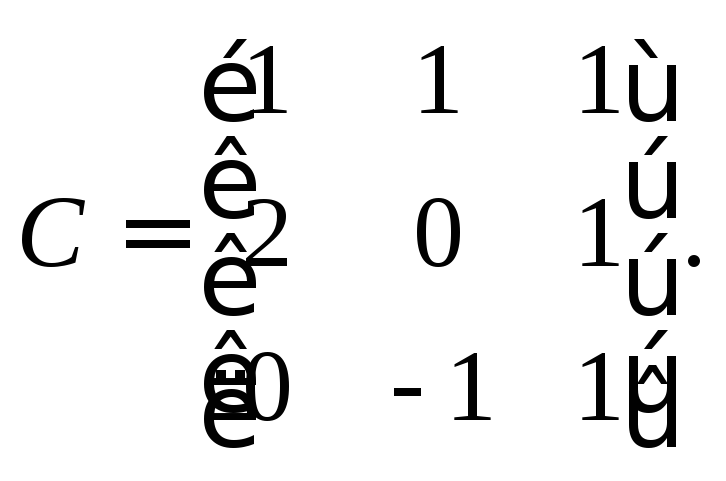
Матрицу B оператора в новом базисе найдем по формуле (23.14).

Находим

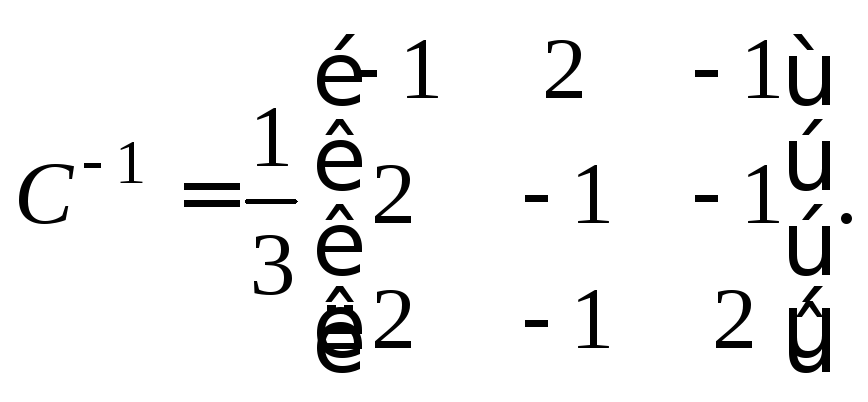
Тогда

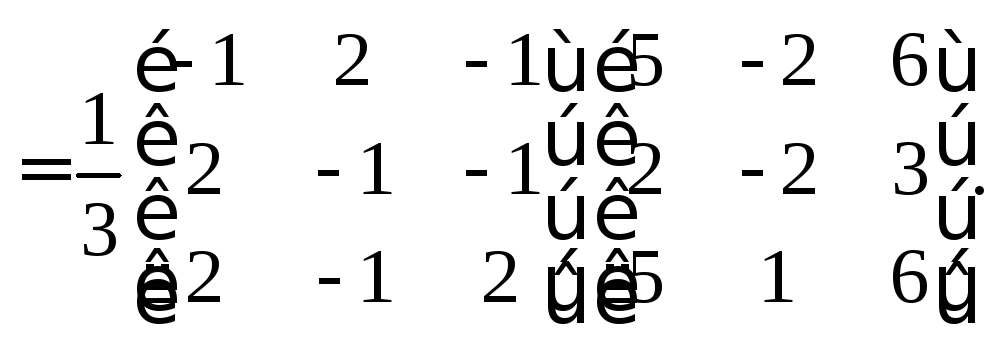
Перемножая матрицы, получаем ответ:

Пример 7. Найти матрицу оператора A в базисе пространстваесли известно, чтоA отображает векторы исоответственно в векторыи

Решение. Из условия имеем иили в матричной формегдеA – искомая матрица оператора A в базисе B – матрица, столбцами которой являются столбцы координат векторов C – матрица, столбцами которой являются столбцы координат векторов соответственно:

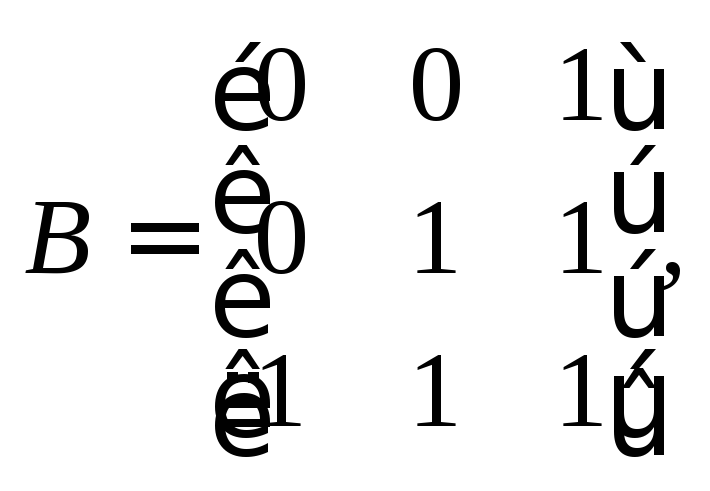
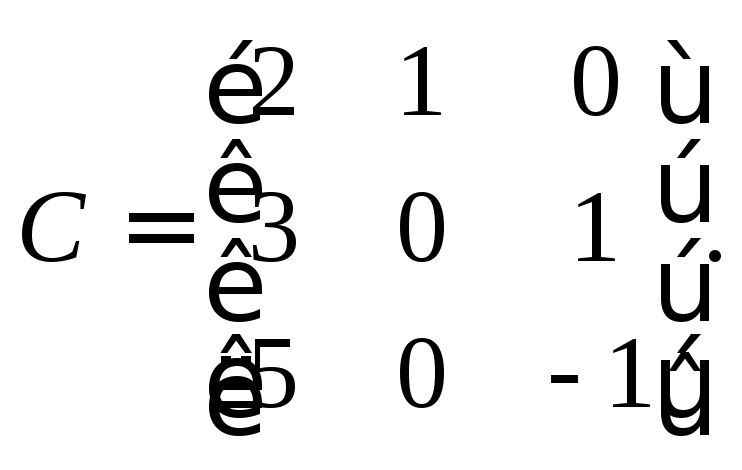
Поскольку то после умножения этого равенства справа наполучаемесли матрицасуществует.

Вычисляем 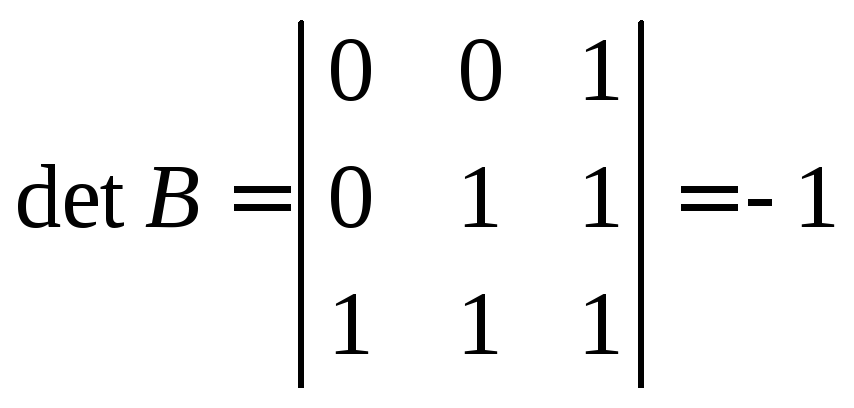и приходим к заключению, чтосуществует.

По правилу нахождения обратной матрицы получаем:

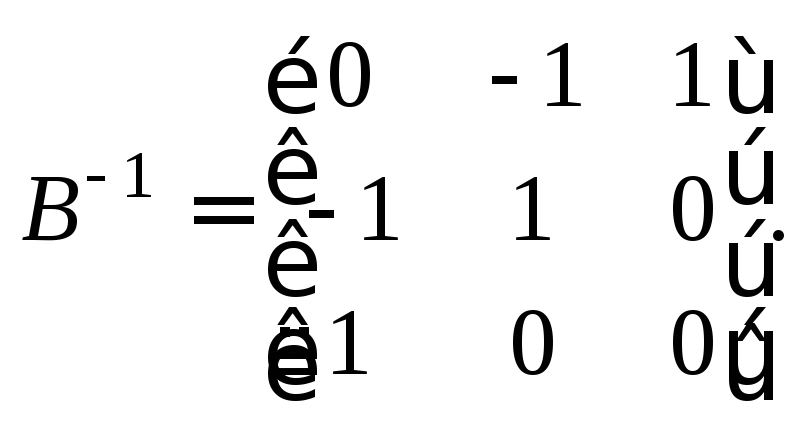
Тогда

Задания