I уровень

1.1.Определите, образует ли следующее множество линейное пространство:

1) множество всех векторов координатной плоскости, выходящих из начала координат и имеющих концы, лежащие в пределах верхней полуплоскости;

2) множество всех целых чисел Z;

3) множество всех действительных чисел R;

4) множество всех матриц-строк

1.2. Определите, образуют ли векторы базис пространстваесли:

1) 2)

3) 4)

5) 6)

1.3. Проверьте, образуют ли векторы базис пространстваЕсли образуют, то найдите координаты векторав этом базисе:

1)

2)

3)

4)

5)

6)

II уровень

2.1.Проверьте, образует ли данное множество векторов подпространство соответствующего линейного пространства:

1) множество всех матриц второго порядка вида в пространстве всех квадратных матриц порядка два;

2) множество всех векторов пространства с рациональными координатами;

3) множество всех векторов пространства с нулевой первой координатой;

4) множество С(R) всех непрерывных и определенных на R функций в пространстве F(R) всех действительных функций, определенных на R.

2.2. Определите, образуют ли векторы базис пространства

1)

2)

3)

4)

2.3. Проверьте, образуют ли векторы базис пространстваЕсли образуют, то найдите координаты векторав этом базисе:

1)

2)

3)

4)

5)

III уровень

3.1.Проверьте, образует ли данное подмножество векторов подпространство соответствующего линейного пространства:

1) множество всех квадратных матриц порядка n у которых сумма элементов равна нулю, в линейном пространстве всех квадратных матриц порядкаn с действительными элементами;

2) множество всех кососимметрических матриц порядка n (матрица A называется кососимметрической, если ) в линейном пространстве всех квадратных матриц порядкаn с действительными элементами.

3.2. Найдите размерность подпространства V векторного пространства где

3.3. Проверьте, образуют ли векторы a, b, c, d базис пространства Если образуют, то найдите координаты вектораf в этом базисе:

23.2. Евклидово пространство, определение

и примеры

Пусть V – линейное пространство. Каждой паре векторов поставим в соответствие действительное число (обозначим (x, y) или ), называемоескалярным произведением векторов x, y и удовлетворяющее следующим аксиомам:

E1) скалярное произведение векторов x, y коммутативно, т. е.

E2) скалярное произведение векторов дистрибутивно относительно сложения векторов, т. е. для любых

E3) числовой множитель можно выносить за знак скалярного произведения, т. е.

E4) скалярный квадрат векторанеотрицателен,т. е. причемтогда и только тогда, когда

Линейное пространство V со скалярным произведением, удовлетворяющим аксиомам E1)–E4), называется евклидовым пространством и обозначается Е, n-мерное евклидово пространство обозначается

Теорема (неравенство Коши–Буняковского). Для любых двух векторов x, y евклидова пространства E справедливо неравенство:

В евклидовом пространстве E для любого вектора x определяется длина (норма) этого вектора:

обладающая следующими свойствами:

D1) если итогда и только тогда, когда

D2)

D3) (неравенство треугольника).

В евклидовом пространстве E для любых векторов x, y определяется угол между векторами x, y, косинус которого находится по формуле:

Два вектора евклидова пространства E называются ортогональными, если их скалярное произведение равно нулю.

Система векторов называется ортогональной, если каждая пара векторов этой системы ортогональна.

Вектор, длина которого равна единице, назывется нормированным. Для любого вектора нормированный векторнаходится по формуле:

Базис евклидова пространствакоторый удовлетворяет условиям(–символ Кронекера), называется ортонормированным базисом.

Базис трехмерного пространства геометрических векторов является ортонормированным.

Пусть – ортонормированный базис пространстваи векторыразлагаются по векторам этого базиса:

Тогда имеем:

(23.3)

(23.4)

(23.5)

Пример 1. Доказать, что евклидовым пространством является:

1) множество всех геометрических векторов если скалярное произведение векторовзадать по формуле

2) множество всех действительных функций, определенных и непрерывных на отрезкесо скалярным произведением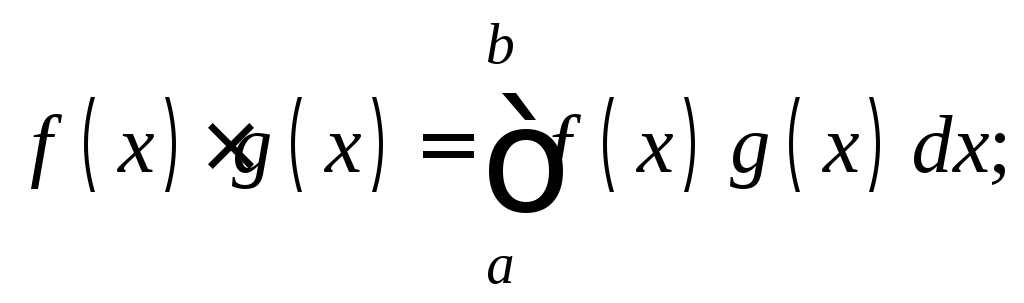

3) арифметическое линейное пространство относительно скалярного произведения, определяемого по формулегде

Решение. Проверка аксиом Е1)–Е4) осуществляется в любом курсе аналитической геометрии.

Выполнение аксиом E1)–E4) следует из свойств определенного интеграла.

Непосредственно проверяется справедливость аксиом E1)–E4).

Пример 2. Доказать, что ортогональная система векторов не содержащая нулевых векторов, состоит из линейно-независимых векторов.

Решение. Пусть тогда

Если тоСледовательно, векторы– линейно-независимые.

Пример 3. Найти угол между векторами ив

Решение. Используя формулы (23.3)–(23.5), находим:

Получаем

Задания