II уровень

2.1. Используя формулу (30.33), найдите оригинал для изображения

1) 2)

3) 4)

2.2. Используя формулы (30.34) и (30.35), найдите оригинал, соответствующий изображению и запишите его в виде степенного ряда:

1) 2)

III уровень

3.1. Найдите изображение функции

1) 2)

3.2. Найдите оригинал изображения и запишите оригинал через цилиндрическую функцию при некотором значении

1) 2)

3.3. Найдите изображение функции

3.4. Найдите изображение функции а затем разложите ее в степенной ряд по степеням

1) 2)

30.6. Восстановление оригинала

для рационального изображения

При восстановлении оригинала для рационального изображения справедливы следующие теоремы.

Теорема 12. Изображение является рациональной функцией тогда и только тогда, когда оригинал является конечной линейной комбинацией функций видагде;

Для нахождения оригинала по известному рациональному изображению поступают так: функцию F (p) раскладывают на сумму простейших дробей, а затем используют свойство линейности и таблицу основных оригиналов и изображений.

Теорема 13. Пусть изображение  правильная рациональная дробь с полюсами Тогда

(30.39)

Если все  простые полюсы и где многочлены без общих корней, то

(30.40)

Т а б л и ц а 30.1

Таблица основных оригиналов и изображений

Номер
1
2
3
4
5
6
7

Окончание табл. 30.1

Номер
8
9
10
11
12
13
14
15

Пример 1. Найти оригинал для изображения

Решение. Функцияявляется правильной рациональной дробью. Разложим ее на сумму простейших дробей:

Найдя коэффициенты A, B, C, D, получаем равенство

Далее, используя свойство линейности изображения и формулы с номерами 9, 10, 4 из табл. 30.1, имеем

Приходим к ответу

Пример 2. Найти оригинал если известно, что его изображение имеет вид

Решение. Рассмотрим два способа решения.

1-й способ. Найдем нули знаменателя функции

Нулями знаменателя будут а также три значения кубического корнят. е.Все они являются простыми полюсами изображенияИспользуя формулы (30.36) и (30.39), найдем

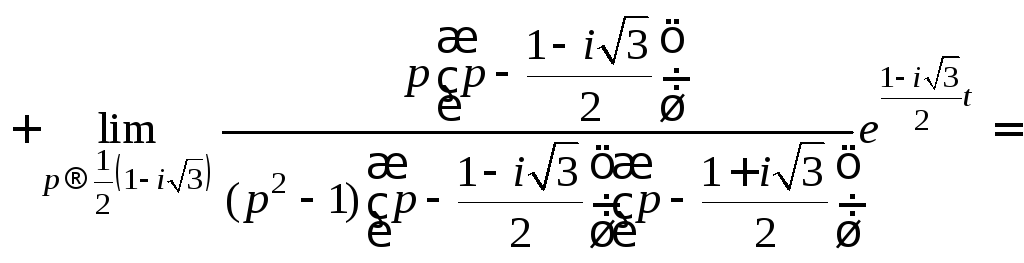
Использовав формулу для (30.38), приходим к ответу

2-й способ. Для решения используем формулу (30.40). По условию Выше было отмечено (1-й способ решения), что все полюсы простые. Многочлены иобщих корней не имеют.

Заметим, что

Применяя формулу (30.40), получаем

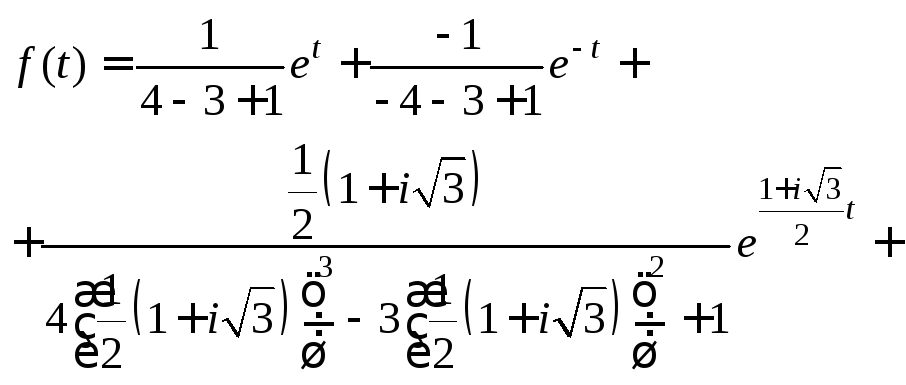
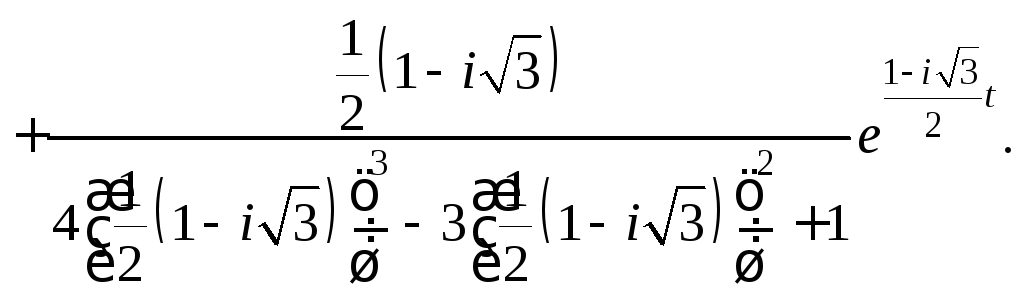
После возведения в степень и упрощения полученного выражения, приходим к тому же ответу:

Заметим, что этот пример можно было решать и третьим способом – разложением на сумму простейших дробей.

Задания