30. Операционное исчисление

30.1. Основные понятия операционного исчисления

Функция f (t) действительной переменной называетсяоригиналом (функцией-оригиналом), если она удовлетворяет следующим условиям:

1) f (t) является кусочно-непрерывной, интегрируемой на любом конечном интервале оси

2) существуют константы такие, что(30.1)

3)

Константу называют показателем роста функции f (t).

Простейшим примером функции-оригинала является единичная функция (функция Хевисайда):

Если некоторая функция f (t) удовлетворяет первым двум условиям функции-оригинала, а третьему условию она не удовлетворяет, то операция умножения ее на функцию Н (t) приводит к оригиналу Н (t) f (t):

Вместо Н (t) f (t) будем писать просто f (t) и всегда понимать, что f (t) = 0 при любом

Изображением функции f (t) называется функция F (р) комплексной переменной которая определяется равенством

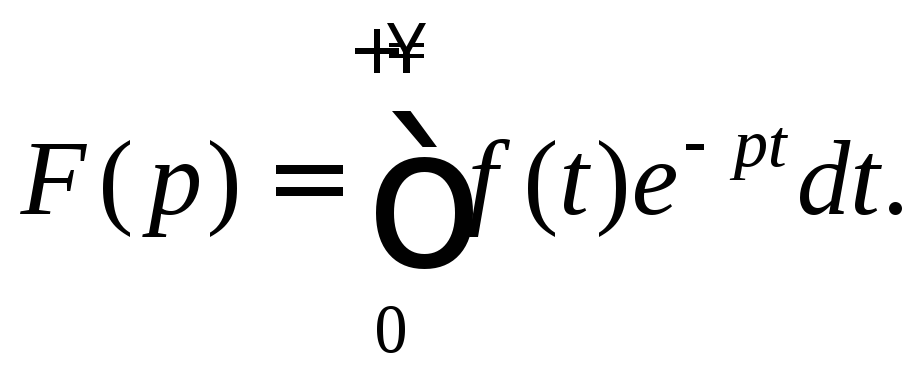(30.2)

Интеграл, входящий в равенство (30.2), называется преобразованием Лапласа, поэтому функцию F (р) называют еще изображением по Лапласу функции f (t).

Словесное выражение «является изображением для оригинала» записывают так:

выражение же «является оригиналом для» записывается так:

Теорема 1. Для любого оригинала соответствующее изображениеявляется аналитической функцией в полуплоскостигде,− показатель роста функции

Если точка стремится к бесконечности так, чтонеограниченно возрастает, то

(30.3)

Замечание. Не всякая функция может быть изображением некоторого оригинала.

Пример 1. Выяснить, является ли оригиналом функция

1) 2)

Решение. 1) В точке функцияимеет разрыв второго рода, т. е. в этой точке она является бесконечно большой функцией. Но тогда условие (30.1) не выполняется, следовательно, функцияне является оригиналом.

2) Для степенной функции с произвольным натуральным показателем n имеем

в чем можно убедиться, например, применив n раз правило Лопиталя. Поэтому, существует константа М такая, что

Это приводит к заключению, что является оригиналом.

Пример 2. Найти изображение данного оригинала:

1)2)3)

Решение. 1) Функция задана двумя значениями, одно из которых является нулевым при всехСогласно сказанному выше, эту функцию будем задавать в видеИспользуя формулу (30.2), получаем

где т. е. для единичной функции

2) Используя формулу (30.2), получаем

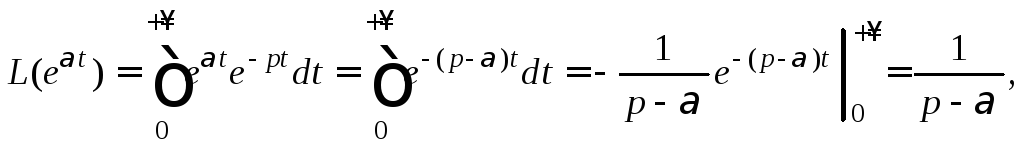
если т. е.то используя формулу (30.2), имеем

3) Используя формулу (30.2) и метод интегрирования по частям, получаем

где Таким образом

Задания

I уровень

1.1. Выясните, является ли оригиналом функция

1) 2)3)

1.2. Найдите изображение функции-оригинала

1) 2)3)4)

II уровень

2.1. Выясните, является ли оригиналом функция

1) 2)3)

2.2. Найдите изображение заданного оригинала

1) 2)3)

4) 5)6)

III уровень

3.1. Найдите изображение функции-оригинала

1) 2)3)

3.2. Покажите, что функция не может быть изображением некоторого оригинала:

1) 2)

30.2. Свойства оригинала и изображения

Оригиналы и изображения имеют следующие свойства.

1. Линейность изображения. Если − оригиналы, то справедливо

(30.4)

для любых констант

2. Свойство подобия. Если то для любого числасправедливо

(30.5)

3. Смещение в области оригинала. Если то для любоговерны формулы

(30.6)

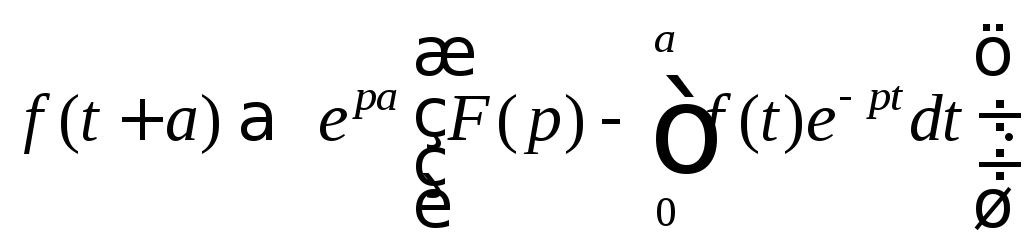(30.7)

З а м е ч а н и е. Для функции f (t) оригинал f (t – а), при является функцией с аргументом, который запаздывает на величину а. Поэтому говорят, что формула (30.6) отражает свойство запаздывания. Аналогично формулу (30.7) рассматривают как свойство опережения.

4. Смещение в области изображения. Если то для любоговерна формула

(30.8)

Сверткой двух функций интегрируемых на бесконечном промежутке , называется функцияопределяемая равенством

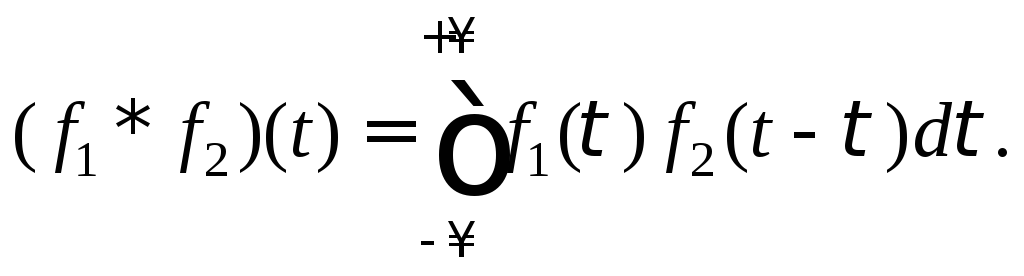(30.9)

Если рассматриваются оригиналы f₁ (t) и f₂ (t), то дляпоэтому формула (30.9) длясвертки оригиналов приобретает вид

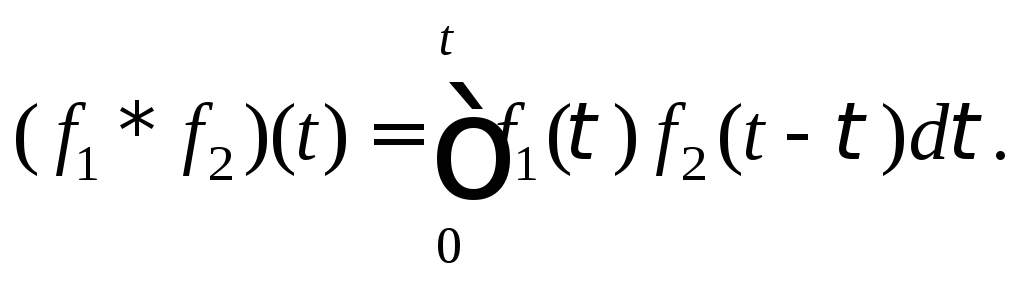(30.10)

Теорема 2. Свертка двух оригиналов является оригиналом.

5. Изображение свертки. Если то верна формула

(30.11)

Пример 1. Найти изображение функции-оригинала f (t):

1) 2)3)4)

Решение. Для нахождения изображения оригинала используем свойство линейности, формула (30.4), и найденное в примере 2, параграф 30.1, с.7 данного пособия, изображение для

1) Согласно формуле которую можно вывести, исходя из формул Эйлера получаем

откуда (30.12)

2) Согласно формуле полученной аналогично, приходим к следующему изображению

откуда (30.13)

3) Используя определение функции sh t и свойство линейности изображения, получаем

т. е. (30.14)

4) На основании определения функции сh t и свойства линейности изображения получаем

откуда (30.15)

Пример 2. Найти изображение оригинала f (t):

1) 2)

3)

Решение. 1) Используя найденное ранее изображение cos t, формула (30.13), и свойство подобия (30.5), получаем

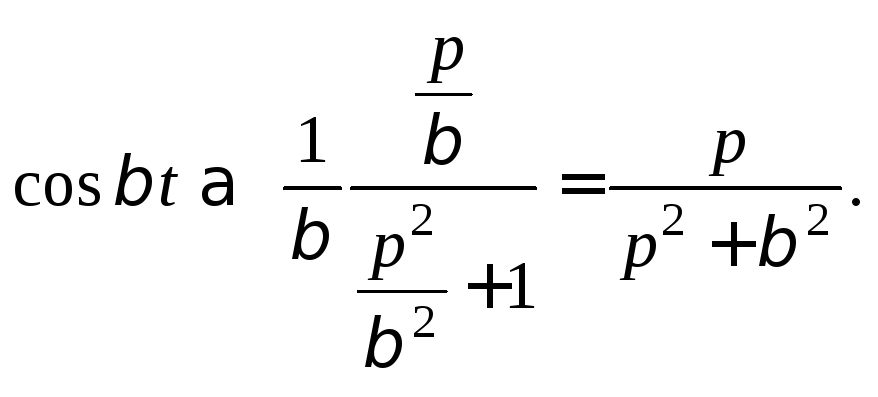(30.16)

2) Применяя формулу (30.12) и свойство смещения в области оригинала, формула (30.6), получаем

3) Аналогично тому, как найдено изображение для , найдем изображение дляформула (30.12):

(30.17)

Применяя формулу (30.6), получаем

Пример 3. Найти изображение оригинала

1) 2)

Решение. 1) Зная, что формула (30.16), и применяя свойство смещения в области изображения, формула (30.8), получаем

2) Зная, что (см. пример 2, параграф 30.1, с.7 данного пособия), аналогично предыдущему решению находим

Пример 4. Найти изображение оригинала

Решение. Функция является ступенчатой (рис. 30.1).

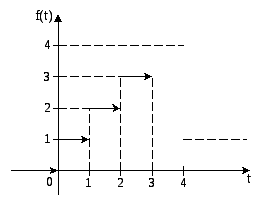
Рис. 30.1

Используя единичную функцию (функцию Хевисайда) (см. пример 2, параграфа 30.1, с.7 данного пособия), функцию можно записать в виде

Как было показано в примере 2, параграф 30.1, с. 7 данного пособия,Тогда согласно свойству линейности изображения, формула (30.4), и в соответствии с формулой (30.6) получаем

По формуле суммы элементов бесконечно убывающей геометрической прогрессии приходим к ответу

Пример 5. Найти оригинал если известно, что соответству­ющее изображениеесть:

1) 2)

3)

Решение. 1) Преобразуем выражение для следующим образом:

Используя формулы (30.8) и (30.17), получаем

Откуда

2) 1-й способ. Как и в предыдущем примере, находим

Применяя формулы (30.8) и (30.14), получаем

Таким образом,

2-й способ. Преобразуем следующим образом:

Так как (см. пример 2, параграф 30.1, с.7 данного пособия), то

Согласно формуле (30.11), получаем

3) Запишем изображение в виде произведения:

Используя формулы (30.12) и (30.13), имеем

Тогда согласно свойству умножения изображений, формула (30.11), получаем

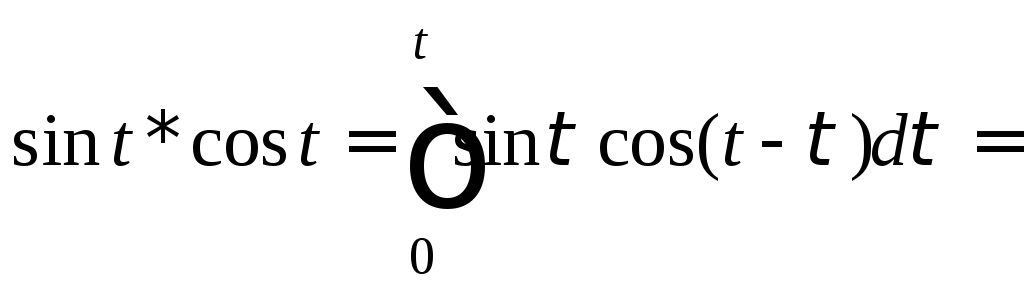
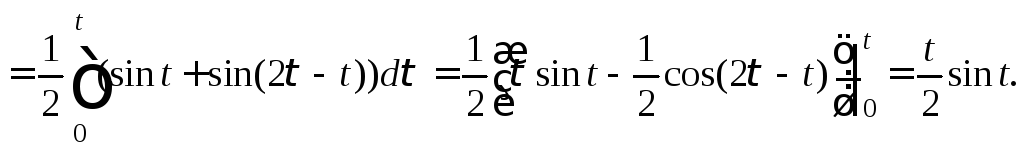
Таким образом, приходим к соотношению

(30.18)

Задания