I уровень

1.1. Пусть −оригинал и Найдите изображениедля функцииесли− оригиналы ив случае:

1) 2)

3) 4)

1.2. Найдите изображение оригинала

1) 2)

3) 4)

II уровень

2.1. Применяя свойство линейности и формулу (30.20), найдите изображение функции-оригинала

1) 2)3)

4) 5)6)

2.2. Найдите оригинал для изображения

1) 2)3)

4) 5)

III уровень

3.1. Найдите оригинал для изображения гдес − константа Эйлера.

3.2. Пусть функция определена на промежуткеравенствами

и продолжена на бесконечный промежуток периодически с периодом 2 (приНайдите изображение функции

30.4. Интегрирование оригиналов и изображений

При интегрировании оригиналов и изображений справедливы следующие теоремы.

Теорема 7 (об интегрировании оригинала). Если то верна формула

(30.28)

Теорема 8 (об интегрировании изображения). Если и интеграл сходится (путь интегрирования лежит в полуплоскостиRe , где– показатель роста функции из формулы (30.1)), то справедлива формула

(30.29)

Теорема 9. Пусть– оригинал, – его изображение. Тогда справедлива формула

(30.30)

где

если оба интеграла сходятся.

С л е д с т в и е. Если , то верна формула

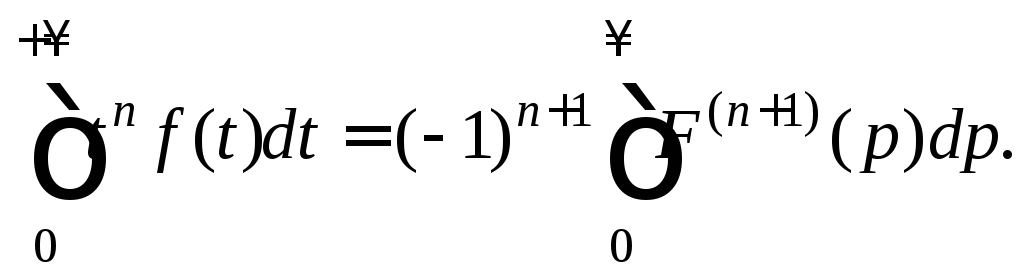(30.31)

Пример 1. Найти оригинал , если известно, что его изображение имеет вид

Решение. Запишем изображение в виде

Известно, что (формула (30.12)). Поэтому, согласно формуле (30.28), получаем

Приходим к ответу

Пример 2. Найти изображение оригинала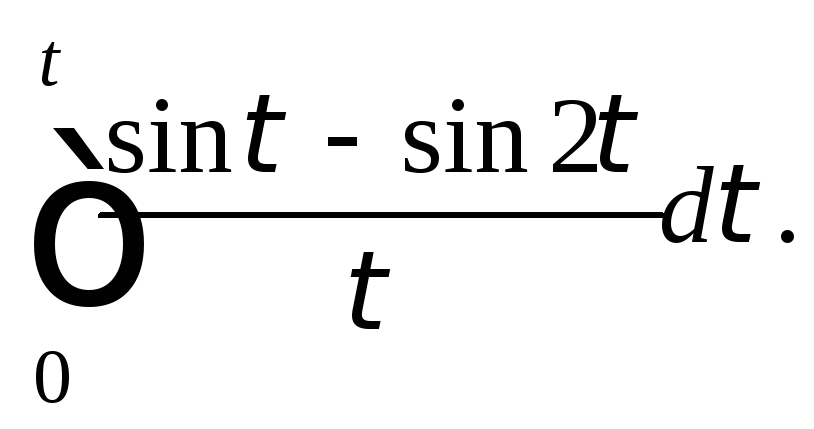

Решение. Используя свойство линейности и формулу (30.17) соот­ветственно для имеем

Делению оригинала на аргумент, согласно теореме 8, соответствует интегрирование изображения:

Теперь используем теорему 7 об интегрировании оригинала, которая и приводит к ответу,

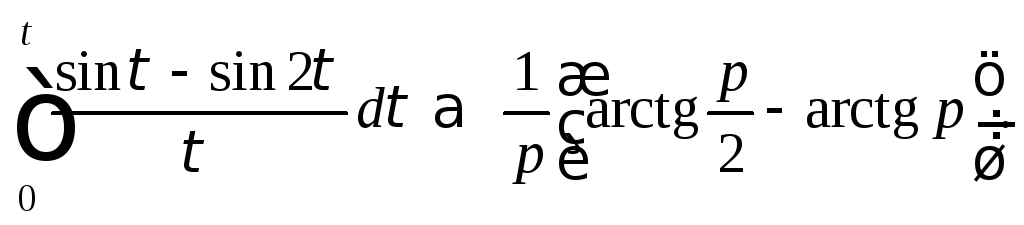
Пример 3. Вычислить интеграл:

1) 2)

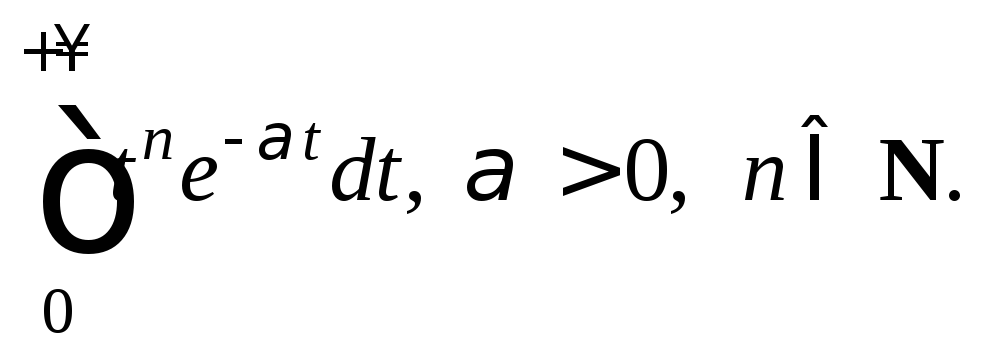
Решение. 1) Используем формулу (30.12):

Согласно равенству (30.30), получаем

2) Используем формулу

(см. пример 2, параграф 30.1, с. 7 данного пособия).

Тогда равенство (30.31) для нашего случая приобретает вид

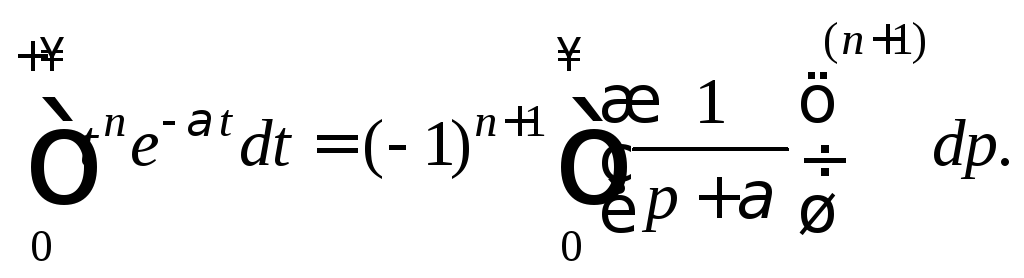
Применяя метод математической индукции, можно убедиться, что n-я производная функции может быть найдена по формуле

Поэтому получаем

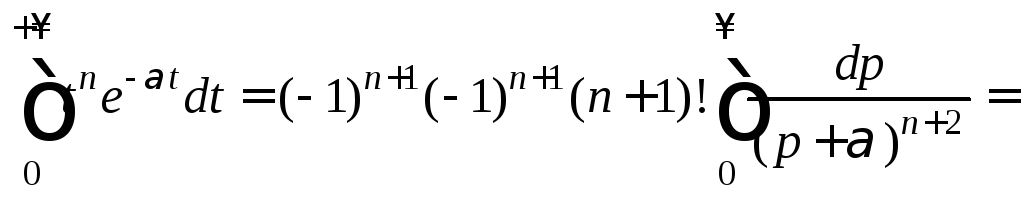
Задания

I уровень

1.1. Используя формулу (30.28), найдите оригинал , если известно, что его изображение имеет вид:

1) 2)3)

4) 5)6)

1.2. Используя формулу (30.29), найдите изображение оригинала

1) 2) 3)

4) 5)

1.3. Вычислите интеграл:

1) 2)

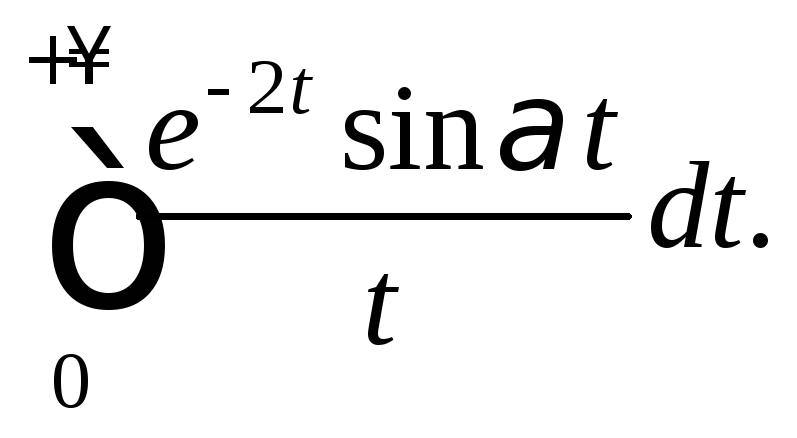
II уровень

2.1. Используя формулу (30.28), найдите оригинал по его изображению

1) 2)

3) 4)

2.2. Используя формулу (30.29), найдите изображение оригинала

1) 2)3)

4) 5)6)

III уровень

3.1. Используя формулу (30.28), найдите оригинал по его изображению

1) 2)

30.5. Обратное преобразование Лапласа.

Теорема о разложении

При обратном преобразовании Лапласа справедлива следующая теорема.

Теорема 10 (формула Меллина или обратное преобразование Лапласа). Если – аналитическая функция в области , равномерно относительнопри,

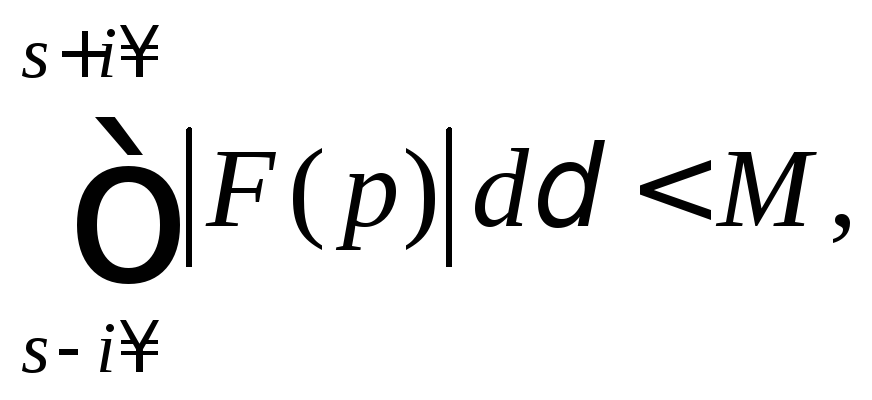
то является изображением функции

(30.32)

где

Интеграл (30.32) по прямой понимается в смысле главного значения (т. е. как предел интеграла по промежутку () при).

Используя для вычисления интеграла теорию вычетов, можно придать формуле (30.32) вид

(30.33)

В формуле (30.33) записана сумма вычетов во всех особых точках функции которые лежат слева от прямой (т. е. слева от прямой интегрирования в формуле (30.32)).

При разложении аналитической функции справедлива следующая теорема

Теорема 11 (о разложении). Если изображение является аналитической функцией в окрестности точки иразлагается в ряд Лорана

(30.34)

причем то ее оригинал имеет вид

(30.35)

и ряд (30.35) сходится при всех

Пример 1. Найти оригинал для изображения

Решение. Для нахождения оригинала можно воспользоваться формулой (30.33). Особыми точками функции F (p) являются точки причеми простые полюсы, и полюсы 2-го порядка. Поскольку все особые точки лежат на мнимой оси, то функция F (p) аналитична на полуплоскости Вычеты в точкахинайдем по формуле

(30.36)

Получим

Вычисление вычетов в точкахвыполним на основе формулы

(30.37)

где a  полюс k-го порядка функции

Получим

Согласно формуле (30.33), получим

Поскольку

(30.38)

то приходим к ответу

Пример 2. Найти оригинал для изображения

Решение. Очевидно, что функция удовлетворяет условиям теоремы 11. Разложив функцию в ряд, используя формулу

получим

Согласно теореме 11, функции соответствует оригинал

Покажем, что этот оригинал выражается через специальную функцию, которая носит название цилиндрической функции. Для этого запишем последний ряд в виде

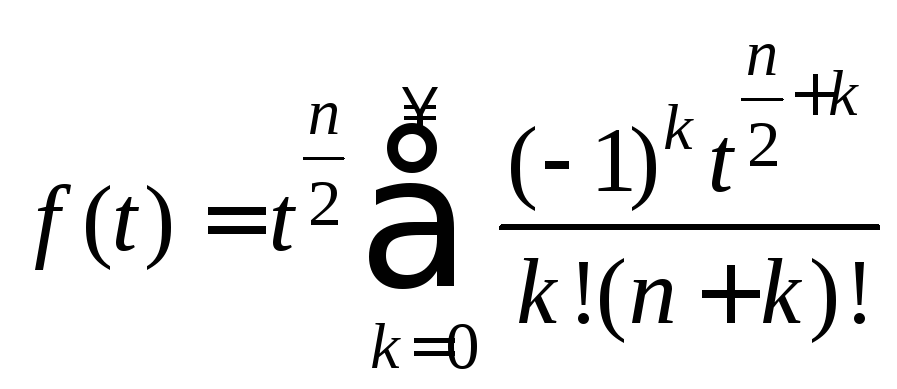
и, сделав замену переменной получим

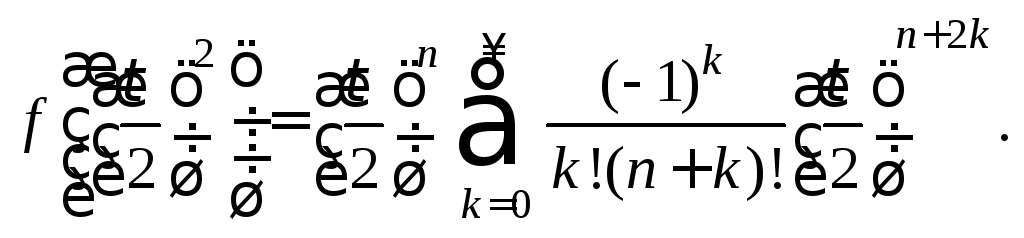
Цилиндрическая функция определяется так:

Используя это обозначение, вернемся к переменной и получим

Таким образом, приходим к ответу

Задания