I уровень

1.1. Найдите изображение функции-оригинала

1) 2)3)

4) 5)6)

1.2. Найдите оригинал если известно, что соответствующее изображениеесть:

1) 2)3)

4) 5)

II уровень

2.1. Найдите изображение функции-оригинала

1) 2)

3) 4)

5) 6)

7)

2.2. Найдите оригинал по известному изображению

1) 2)

3) 4)

5) 6)

7) 8)

9)

10)

III уровень

3.1. Найдите изображения оригинала

1) 2)

3) 4)

3.2. Найдите оригинал по известному изображению

1) 2)

3)

3.3. Известно, что Докажите, чтои выясните причину несовпадения изображений этих оригиналов.

30.3. Дифференцирование оригиналов и изображений

Для дифференцирования оригиналов и изображений справедливы следующие теоремы.

Теорема 3 (о производной оригинала). Если и− оригиналы ито верна формула

(30.19)

где

Далее будем обозначать

С л е д с т в и е. Если …,− оригиналы ито справедлива формула

(30.20)

где понимается аналогично

В частном случае, когда

соотношение формулы (30.20) приобретает вид

(30.21)

Теорема 4 (о производной изображения). Если то верна формула

(30.22)

С л е д с т в и е. Если то справедлива формула

(30.23)

Теорема 5. Пусть − непрерывный оригинал,− оригинал с непрерывной производнойиТогда справедлива формула Дюамеля

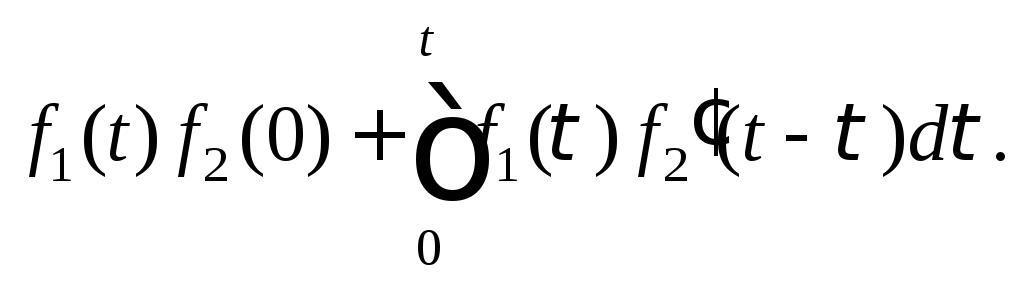(30.24)

Теорема 6. Если функция и ее производнаяявляются оригиналами ито

(30.25)

где внутри угла(− произвольный малый угол,) и

Если же то

(30.26)

где внутри угла

Пример 1. Пусть − оригинал,Найти изображениедля функцииесли− оригиналы, причем

Решение. Согласно формуле (30.20), имеем

Свойство линейности, формула (30.4), приводит к соотношению

Получаем

Пример 2. Найти изображение оригинала

1) 2)

Решение. Используем формулы (30.22), (30.23), записав их в виде

1) Согласно формуле (30.16), имеем

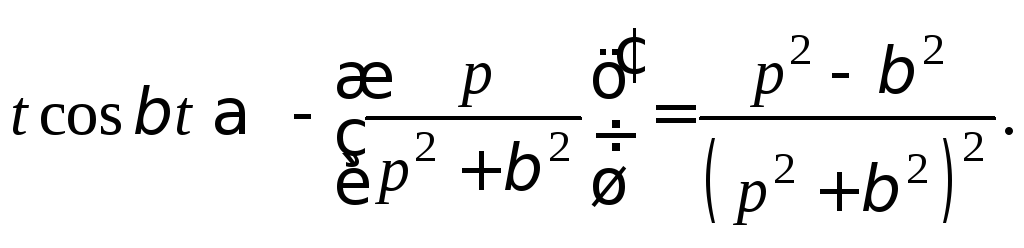
2) Применяя формулы (30.5) и (30.14), находим

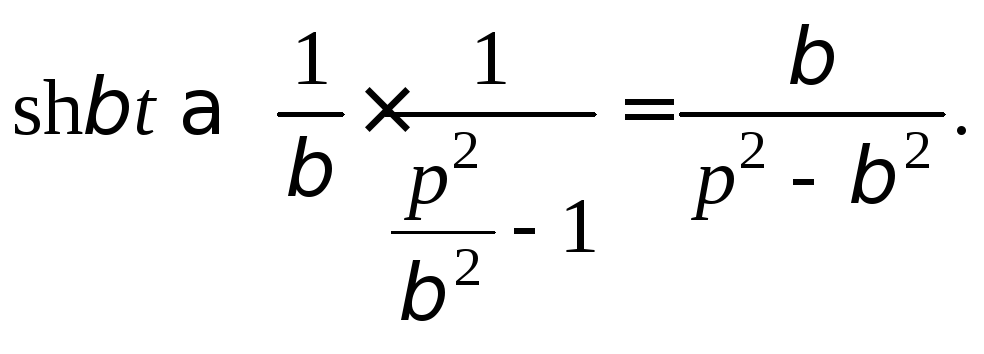Тогда

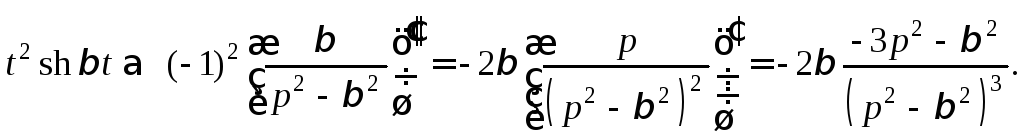
Значит,

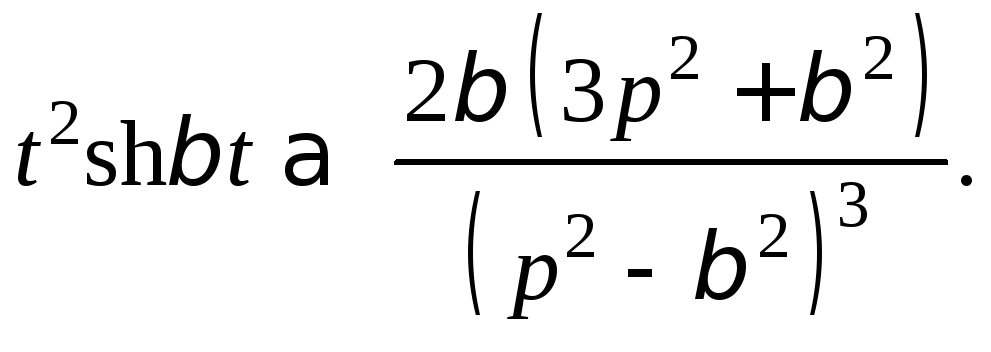
Пример 3. Найти изображение функции

Решение. Обозначим искомое изображение через

Согласно формуле дифференцирования изображения (30.22), имеем Используя свойство линейности, формула (30.4), и соотношение

(см. пример 2, параграф 30.1, с. 7 данного пособия), на­ходим

Продифференцируем оригинал в соответствии с формулой (30.19):

причем, согласно правилу Лопиталя, имеем

Поэтому получаем

Так как то имеем соотношение

которое означает

так как

Из последнего равенства найдем Очевидно, что

Выполнив интегрирование

найдем

(30.27)

(рассматриваем только главное значение логарифма

При равенство (30.27) дает

Поскольку то получаем

Известно, что

Число называютконстантой Эйлера.

Таким образом, приходим к ответу

где − константа Эйлера.

Пример 4. Найти оригинал для изображения

Решение. Запишем в виде, который соответствует левой части равенства (30.24):

Известно, что (формулы (30.12), (30.13))

Тогда, согласно формуле Дюамеля (30.24), имеем

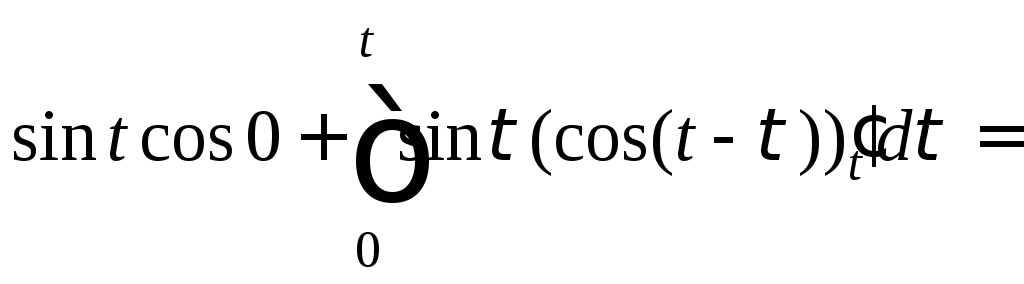
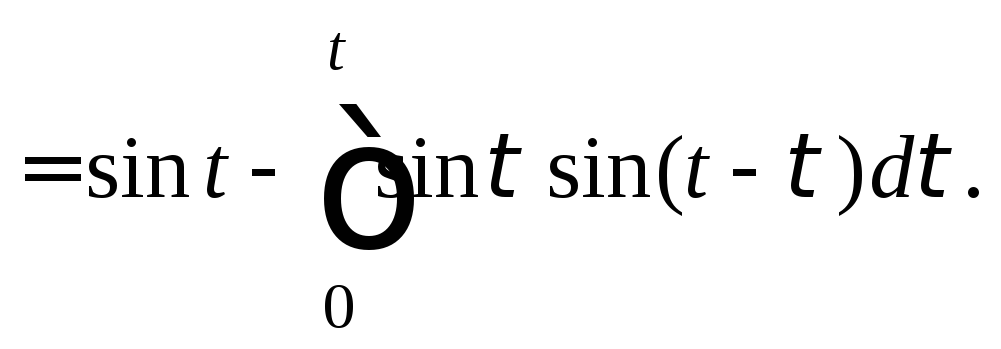
Вычислив последний интеграл

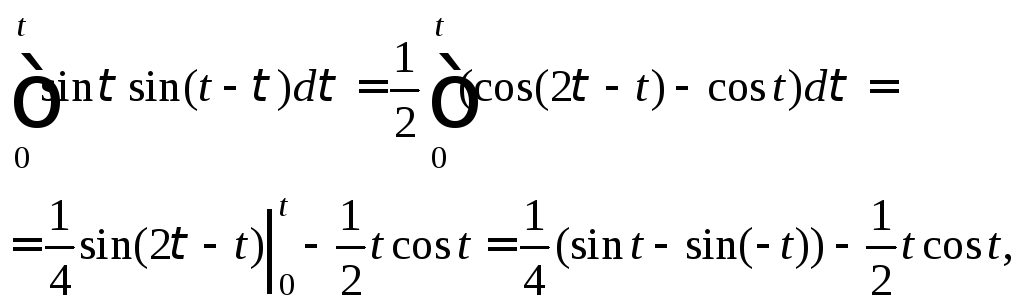
приходим к ответу

Задания