I уровень

1.1. С помощью метода последовательного дифференцирования найдите первые три члена разложения в ряд частного решения дифференциального уравнения удовлетворяющего начальному условию

1.2. Методом последовательного дифференцирования найдите первые три члена разложения в ряд частного решения дифференциального уравнения удовлетворяющего начальным условиям

1.3. С помощью метода последовательного дифференцирования найдите частное решение дифференциального уравнения удовлетворяющего начальным условиям

1.4. Используя метод неопределенных коэффициентов, найдите три первых, отличных от нуля, члена разложения в ряд частного решения дифференциального уравнения удовлетворяющего начальному условию

1.5. Методом неопределенных коэффициентов найдите первые четыре члена разложения в ряд частного решения дифференциального уравнения удовлетворяющего начальным условиям

1.6. С помощью метода неопределенных коэффициентов найдите частное решение дифференциального уравнения удовлетворяющего начальному условию

1.7. Методом Эйлера найдите пять значений функции определяемой уравнениемпри начальном условииполагая

1.8. Методом Эйлера найдите решение задачи Коши в первых пяти точках отрезкапринимая

1.9. С помощью метода Эйлера найдите численное решение дифференциального уравнения на отрезкепри начальном условииполагая

II уровень

2.1. Методом последовательного дифференцирования найдите первые три, отличные от нуля, члена разложения в ряд частного решения дифференциального уравнения удовлетворяющего начальным условиям

2.2. Используя метод последовательного дифференцирования, найдите частное решение дифференциального уравнения удовлетворяющее начальным условиям

2.3. С помощью метода последовательного дифференцирования найдите общее решение дифференциального уравнения

2.4. Применяя метод последовательного дифференцирования, найдите частное решение системы дифференциальных уравнений 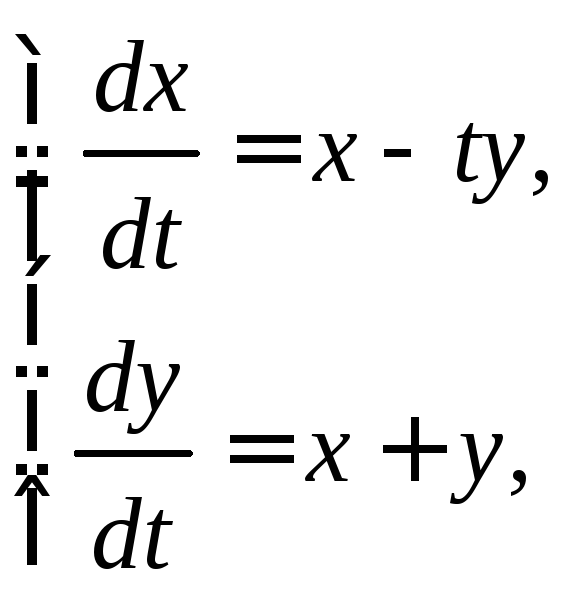удовлетворяющее начальным условиямограничившись тремя-четырьмя, отличными от нуля, членами.

2.5. Методом неопределенных коэффициентов найдите первые четыре, отличные от нуля, члена разложения в ряд частного решения дифференциального уравнения удовлетворяющего начальному условию

2.6. С помощью метода неопределенных коэффициентов найдите частное решение дифференциального уравнения удовлетворяющее начальным условиям

2.7. С помощью метода неопределенных коэффициентов найдите общее решение дифференциального уравнения

2.8. Методом Эйлера найдите решение задачи Коши на отрезкеполагая

III уровень

3.1. Найдите три первых, отличных от нуля, члена разложения в степенной ряд решения дифференциального уравнения удовлетворяющего начальному условию

3.2. Найдите первые пять, отличные от нуля, членов разложения в степенной ряд решения дифференциального уравнения удовлетворяющего начальным условиям

3.3. Найдите общее решение дифференциального уравнения методом интегрирования с помощью рядов.

3.4. Найдите решение дифференциального уравнения удовлетворяющее начальным условиямв виде многочлена на отрезкес погрешностью, не превышающей

3.5. Найдите общее решение системы дифференциальных уравнений 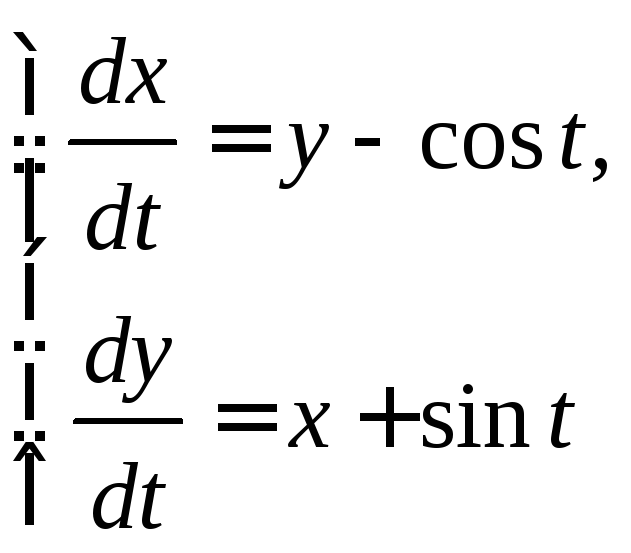методом интегрирования с помощью рядов.

3.6. Составьте алгоритмическую схему приближенного решения задачи Коши для дифференциального уравнения первого порядка методом Эйлера.

приложения