I уровень

1.1. С помощью степенных рядов вычислите интеграл с точностью до

1) 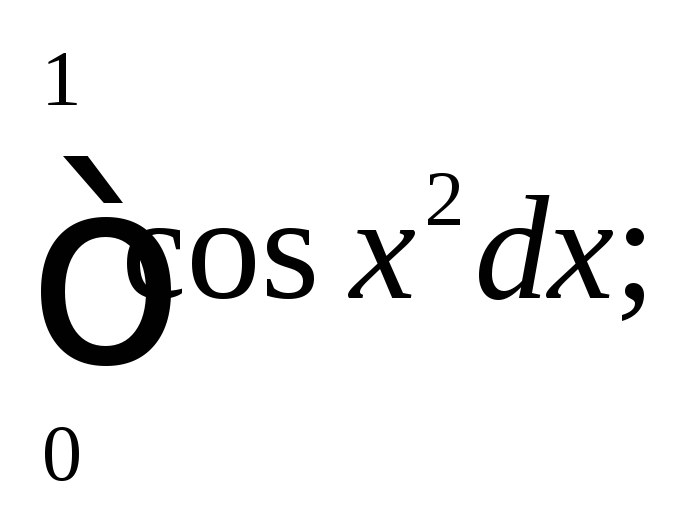2)

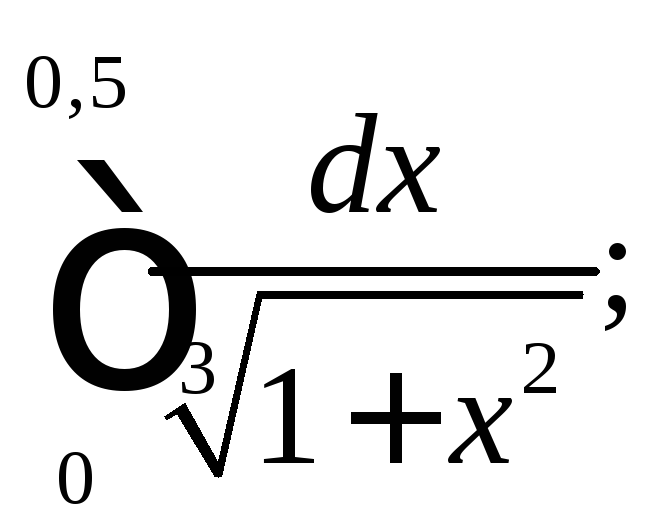3) 4)

1.2. Пользуясь формулой левых прямоугольников при вычислите

1.3. Пользуясь формулой правых прямоугольников при вычислите

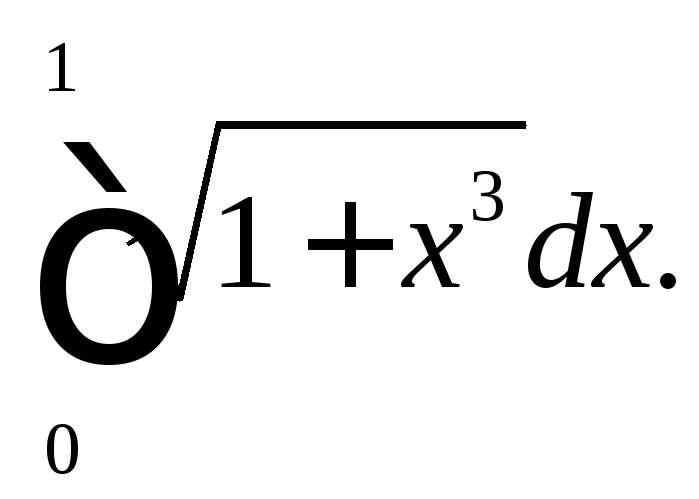
1.4. Используя формулу средних прямоугольников при вычислите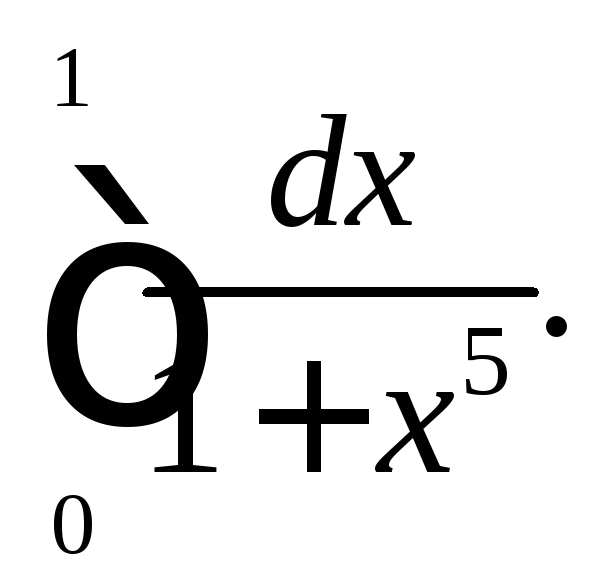

1.5. С помощью формулы трапеций при вычислитеи определите абсолютную и относительную погрешности результата, зная точное значение интеграла.

1.6. С помощью формулы Симпсона при вычислитеи определите абсолютную и относительную погрешности результата, зная точное значение интеграла.

1.7. Определите, на сколько частей нужно разбить промежуток интегрирования, чтобы по формулам левых и правых прямоугольников с точностью до вычислить

1.8. Определите, на сколько частей следует разбить промежуток интегрирования, чтобы по формуле средних прямоугольников с точностью до вычислить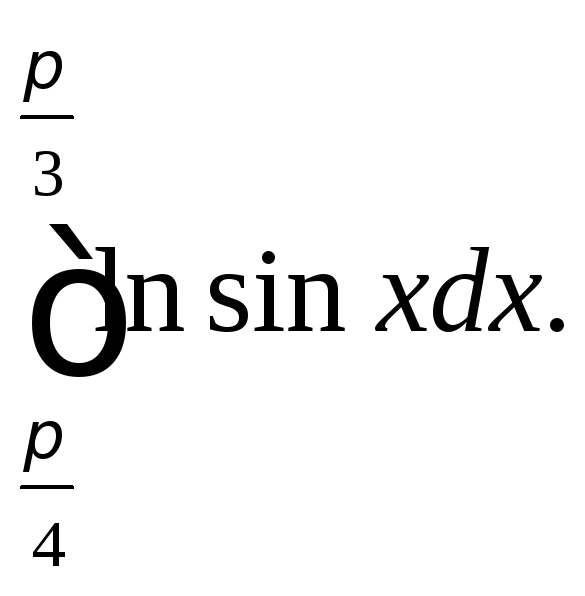

1.9. Определите, на сколько частей следует разбить промежуток интегрирования, чтобы по формуле трапеций с точностью до вычислить

1.10. Ширина реки равна 20 м. Замеры глубины в поперечном сечении реки через каждые 2 м дали следующие результаты, указанные в следующей таблице:

	0	2	4	6	8	10	12	14	16	18	20
	0,4	0,8	1,1	1,4	1,8	2,1	2,4	1,9	1,5	0,9	0,5

Здесь через x обозначено расстояние от одного из берегов, а через y – соответствующая глубина реки. Требуется найти площадь поперечного сечения реки.

II уровень

2.1. С помощью разложения подынтегральной функции в степенной ряд вычислите 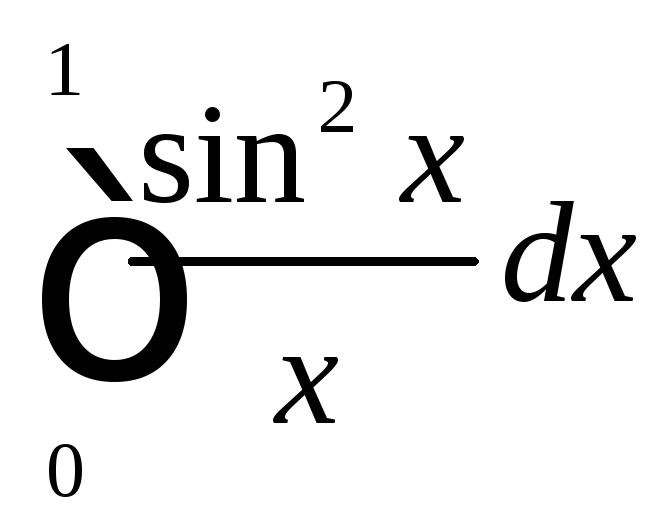с точностью до

2.2. Вычислите 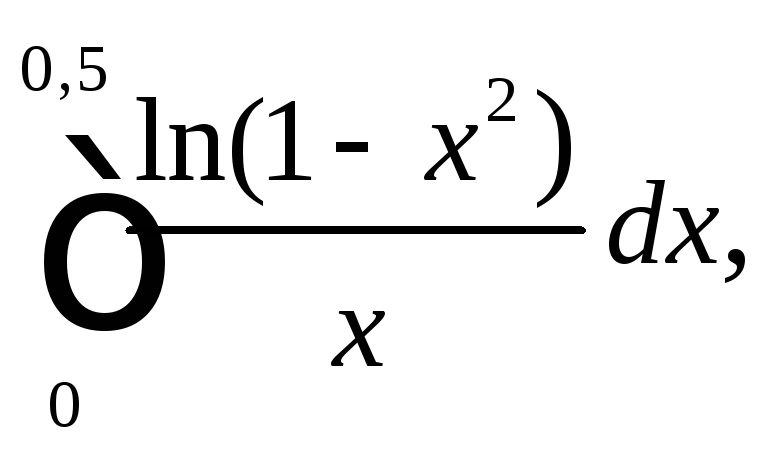разлагая подынтегральную функцию в степенной ряд и используя три члена этого разложения. Определите абсолютную погрешность результата.

2.3. Вычислите с помощью формул левых и правых прямоугольников интеграл 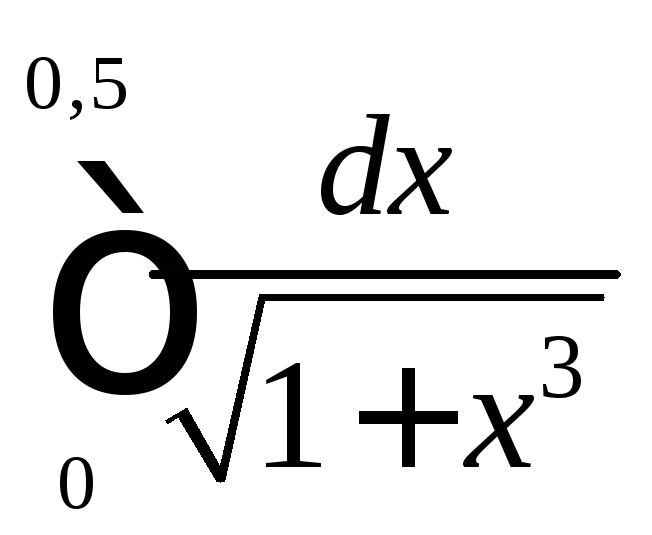с точностью до

2.4. Вычислите с точностью дос помощью формулы средних прямоугольников.

2.5. Вычислите с точностью дос помощью формулы трапеций.

2.6. Вычислите с точностью дос помощью формулы Симпсона.

2.7. Найдите с точностью до длину дуги косинусоиды

2.8. Найдите с точностью до длину дуги лемнискаты Бернулли

III уровень

3.1. Вычислите с точностью допутем разложения подынтегральной функции в функциональный ряд.

3.2. По формуле левых прямоугольников вычислите приняви определите абсолютную погрешность результата.

3.3. По формуле правых прямоугольников вычислите 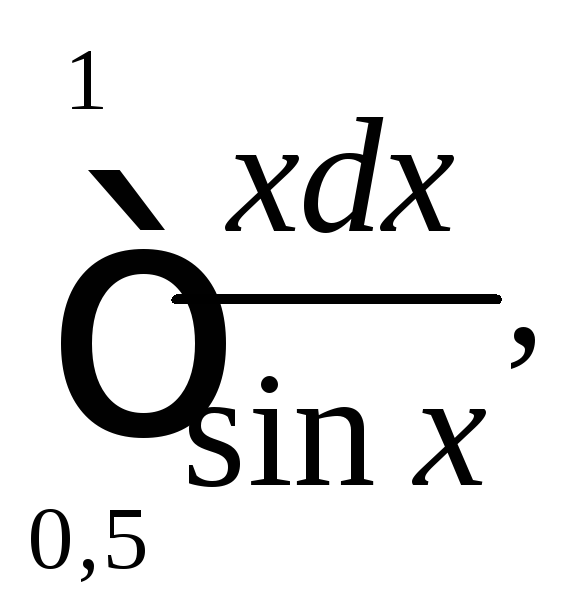принявиопределите абсолютную погрешность результата.

3.4. По формуле средних прямоугольников вычислите полагаяи определите абсолютную погрешность результата.

3.5. Пользуясь формулой трапеций при вычислитеи определите абсолютную погрешность результата.

3.6. Пользуясь формулой Симпсона при вычислитеи определите абсолютную погрешность результата.

3.7. Найдите с точностью до площадь фигуры, ограниченной кривойпрямымии осьюOx.

3.8. Составьте алгоритмическую схему приближенного вычисления определенного интеграла от функции, заданной таблично, по формулам левых и правых прямоугольников.

3.9. Составьте алгоритмическую схему приближенного вычисления определенного интеграла от функции, заданной таблично, по формуле средних прямоугольников.

3.10. Составьте алгоритмическую схему приближенного вычисления определенного интеграла от функции, заданной таблично, по формуле трапеций.

3.11. Составьте алгоритмическую схему приближенного вычисления определенного интеграла от функции, заданной таблично, по формуле Симпсона.