33.2. Аппроксимация функций

Пусть требуется данную функцию приближенно заменить (аппроксимировать) некоторой функцией , называемой аппроксимирующей, так, чтобы отклонение от в заданной области было наименьшим.

В качестве аппроксимирующей функции чаще всего используется многочлен вида

(33.7)

где

Аппроксимация может быть непрерывной или точечной. Аппроксимация называется непрерывной, если аппроксимирующая функция строится на некотором промежутке числовой оси. Аппроксимация называется точечной, если строится на заданном дискретном множестве точек

Вычисление значений функций с помощью рядов

Пусть требуется вычислить приближенное значение аналитической на отрезке функции в точке Разложим функцию в ряд Тейлора в окрестности некоторой точки и в качестве аппроксимирующей функции возьмем многочлен Тейлора n-й степени:

Для определения абсолютной погрешности приближенного значения необходимо оценить остаточный член

(33.8)

числового ряда

(33.9)

Если ряд (33.9) знакочередующийся, члены которого удовлетворяют условиям признака Лейбница, то используется оценка где– модуль первого члена ряда (33.8). В случае знакопостоянного ряда (33.9) остаточный член обычно сравнивают с бесконечно убывающей геометрической прогрессией.

Интерполирование функций

Предположим, что в точках заданы значения некоторой функции определенной на отрезке Тип точечной аппроксимации, основанный на критерии совпадения функций и на заданном дискретном множестве точек на котором определена функция называется интерполированием (или интерполяцией). Точки называются узлами интерполяции.

Различают два вида интерполяции: глобальную и локальную. Интерполяция называется глобальной, если для дан- ной функции требуется найти (единственный!) многочлен степени n, принимающий в заданных различных точках те же значения , что и функция , т. е.

(33.10)

Многочлен удовлетворяющий условиям (33.10), называется интерполяционным многочленом. Величина называетсяостаточным членом интерполяционного многочлена (или погрешностью интерполяции).

При иинтерполяция называется соответственнолинейной и квадратичной.

Многочлен вида

(33.11)

называется интерполяционным многочленом Лагранжа.

Если функция имеет на отрезке непрерывную производную (n + 1)-го порядка, то верна следующая оценка ос­таточного члена многочлена Лагранжа:

(33.12)

где

Интерполяция называется локальной (или кусочной), если интерполяционные многочлены строятся отдельно для разных частей рассматриваемого интервала изменения x.

Метод наименьших квадратов

Пусть данные некоторого опыта представлены таблицей значений Требуется найти приближенную зависимость

(33.13)

значения которой при мало отличаются от опытных данных Приближенная функциональная зависимость (33.13), полученная на основании экспериментальных данных, называется эмпирической формулой.

Мерой близости функций и на множестве точек присреднеквадратичном приближении является величина S, определяемая равенством

где – постоянные параметры. При этом случайсоответствует интерполяции.

Метод наименьших квадратов состоит в том, что параметры эмпирической формулы (33.13) находятся из условия минимума функции

Если функция ищется в виде многочлена (33.7), то соответствующая система уравнений для отыскания коэффициентов многочлена называетсянормальной и имеет вид

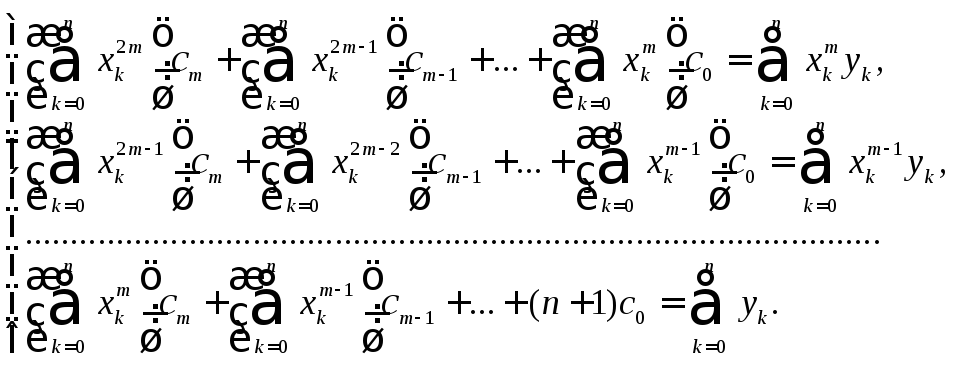
При нормальная система уравнений запишется в виде

(33.14)

Возможность использования линейной зависимости можно проверить путем вычисления значений

При в качестве эмпирической формулы может быть выбранау = ах + b.

Пример 1. С помощью степенного ряда вычислить с точностью до∆ = 10^{– 6}.

Решение. Очевидно, что

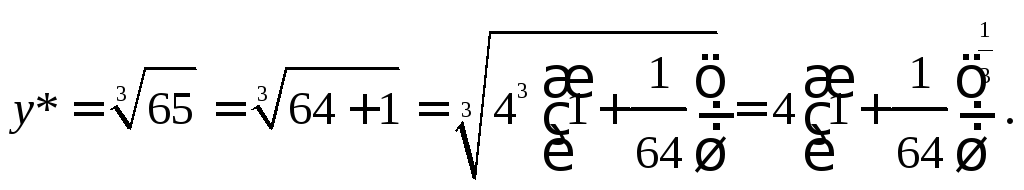
Воспользуемся биномиальным рядом

Полагая в нем получаем

Полученный числовой ряд, начиная со второго члена, является знакочередующимся рядом, удовлетворяющим условиям признака Лейбница. Так как

но то отсюда имеем оценку остаточного члена:

Поэтому для обеспечения заданной степени точности достаточно взять три члена ряда:

Следовательно,

Пример 2. С помощью степенного ряда вычислить с точностью до ∆ = 10^{– 4}.

Решение. Воспользуемся разложением функции в ряд Маклорена

при х = – 0,2:

Определим n, используя остаточный член полученного числового ряда:

Путем подбора значений n находим, что для n = 3

Поэтому здесь достаточно взять четыре члена ряда:

Следовательно,

Пример 3. Найти интерполяционный многочлен Лагранжа для функции заданной в виде таблицы:

		0
	0	1		0

Определить абсолютную погрешность интерполяционного многочлена при

Решение. Применяя формулу (33.11) при получим:

Итак,

Оценим остаточный член многочлена Лагранжа по формуле (33.12) при иТак как

то

Следовательно, искомая абсолютная погрешность равна ∆ = 0,016.

Пример 4. Методом наименьших квадратов найти эмпирическую формулу, отвечающую таблице:

x	0	1	2	3	4
	2	5	8,5	11,5	15

Решение. Поскольку здесь – равноотстоящие точкито достаточно вычислить разностиТак как эти разности мало отличаются друг от друга, то в качестве эмпирической формулы можно принять линейную зависимость

Результаты вычислений представлены в таблице:

0 1 2 3 4	0 1 2 3 4	2 5 8,5 11,5 15	0 5 17 34,5 60	0 1 4 9 16
	10	42	116,5	30

Нормальная система уравнений (33.14) в данном случае принимает вид:

Решая эту систему, находим: Следовательно, искомая эмпирическая формула есть

Задания