
- •19. Неопределенный интеграл
- •19.1. Свойства неопределенного интеграла. Таблица
- •I уровень
- •I уровень
- •II уровень
- •III уровень
- •19.3. Интегрирование некоторых выражений,
- •I уровень
- •II уровень
- •III уровень
- •19.4. Метод интегрирования по частям
- •I уровень
- •II уровень
- •III уровень
- •19.5. Рациональные функции. Интегрирование
- •I уровень
- •II уровень
- •III уровень
- •19.6. Интегрирование тригонометрических выражений
- •I уровень
- •II уровень
- •III уровень
- •19.7. Интегрирование иррациональных функций
- •I уровень
- •II уровень
- •III уровень
- •19.8. Интегралы от дифференциальных биномов
- •I уровень
- •II уровень
- •III уровень
I уровень
1.1. Найдите неопределенный интеграл, преобразовав произведение тригонометрических функций в сумму:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
1.2.Найдите
неопределенный интеграл, применяя
подстановку![]() или
или![]()
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)![]() 6)
6)![]()
7)
![]() 8)
8)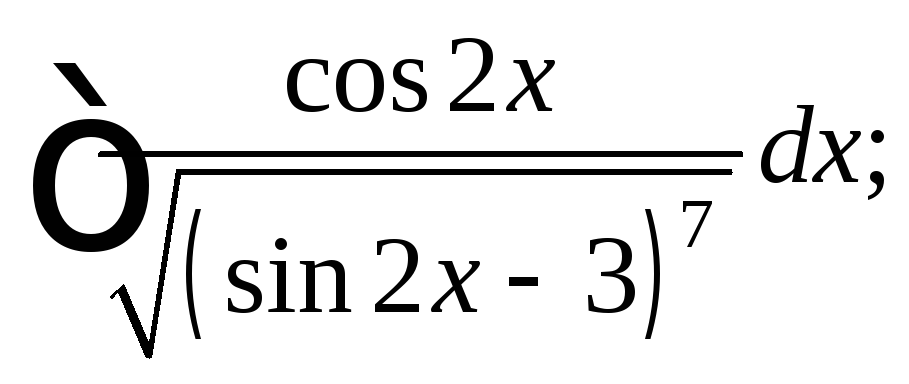 9)
9)![]()
1.3.Найдите неопределенный интеграл, используя формулы понижения степени:
1)
![]() 2)
2)![]() 3)
3)![]()
1.4.Найдите неопределенный интеграл, используя универсальную тригонометрическую подстановку:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
1.5.Найдите
неопределенный интеграл, используя
подстановку![]()
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
II уровень
2.1.Найдите неопределенный интеграл:
1)
![]() 2)
2)![]()
2.2.Найдите
неопределенный интеграл, применяя
подстановку![]() или
или![]()
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
10)
![]() 11)
11)
![]() 12)
12)
![]()
2.3.Найдите
неопределенный интеграл, применяя
подстановку![]() или
или![]()
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
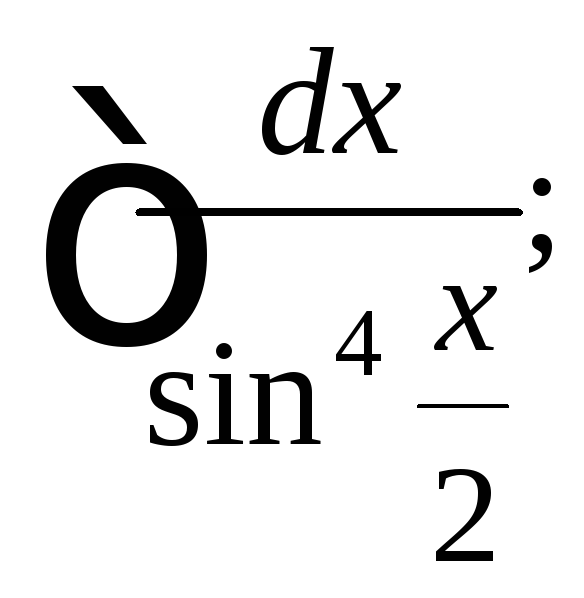 5)
5)![]() 6)
6)
![]()
7)
![]() 8)
8)![]() 9)
9)
![]()
10)
![]() 11)
11)
![]() 12)
12)
![]()
2.4.Найдите
неопределенный интеграл, применяя
подстановку![]() или
или![]()
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)![]()
2.5.Найдите
неопределенный интеграл, применяя
подстановку![]() или
или![]()
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]() 7)
7)
![]() 8)
8)
![]()
2.6.Найдите неопределенный интеграл:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
III уровень
3.1.Найдите неопределенный интеграл, используя универсальную тригонометрическую подстановку:
1)
![]() 2)
2)![]() 3)
3)
![]()
4)
![]() 5)
5)![]() 6)
6)![]()
7)
![]() 8)
8)![]() 9)
9)![]()
10)
![]() 11)
11)![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
3.2.Найдите
неопределенный интеграл, используя
подстановку![]()
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
![]() 8)
8)![]()
9)
![]() 10)
10)![]()
19.7. Интегрирование иррациональных функций
Основной метод вычисления интеграла от иррациональной функции – метод рационализации (т. е. сведение к рациональной функции), для чего делают определенную подстановку.
Алгебраическая подстановка
Интеграл вида
 (19.31)
(19.31)
где
![]() – целые ненулевые числа, с помощью
подстановки
– целые ненулевые числа, с помощью
подстановки
![]()
![]()
приводится к интегралу от рациональной функции.
Частные случаи интеграла(19.31):
1. Если
![]()
![]() то интеграл имеет вид:
то интеграл имеет вид:
![]()
и преобразуется
в интеграл от рациональной функции с
помощью подстановки
![]() где
где![]()
2. Если
![]() ,
,![]() ,
то интеграл (19.31) имеет вид:
,
то интеграл (19.31) имеет вид:
![]()
и сводится к
интегралу от рациональной функции с
помощью подстановки
![]() где
где![]()
Тригонометрическая подстановка
Интегралы вида
![]()
где R– некоторая рациональная функция
относительноxи![]() могут быть вычислены с помощью
тригонометрических подстановок, которые
приводят его к интегралу от рациональной
функции.
могут быть вычислены с помощью
тригонометрических подстановок, которые
приводят его к интегралу от рациональной
функции.
В квадратном
трехчлене выделим полный квадрат
![]() и применим подстановку
и применим подстановку![]() В результате под корнем получим одно
из 3-х выражений:
В результате под корнем получим одно
из 3-х выражений:![]()
![]() или
или![]()
Если имеем
![]() то для уничтожения иррациональности
применим подстановку
то для уничтожения иррациональности
применим подстановку![]() в результате которой
в результате которой![]()
![]() Аналогично можно использовать подстановку
Аналогично можно использовать подстановку![]()
Если имеем
![]() то для уничтожения иррациональности
применяется подстановка
то для уничтожения иррациональности
применяется подстановка![]() в результате которой имеем:
в результате которой имеем:![]()
![]()
Если под интегралом
есть выражение
![]() то подставляем
то подставляем![]() т. е.
т. е.![]()
![]()
Далее интеграл вычисляют как интеграл от тригонометрической функции и возвращаются к старой переменной, выражая последовательно tчерезyиx.
Пример 1. Найти неопределенный интеграл:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
Решение.
1) Поскольку интеграл имеет вид:
![]() а
а![]() то применим подстановку
то применим подстановку![]() Тогда
Тогда
![]()
![]()
![]()
2)
Интеграл имеет вид:
![]() поэтому применим подстановку
поэтому применим подстановку![]() Тогда имеем:
Тогда имеем:

![]()
![]()
![]()
3)
Интеграл имеет вид:
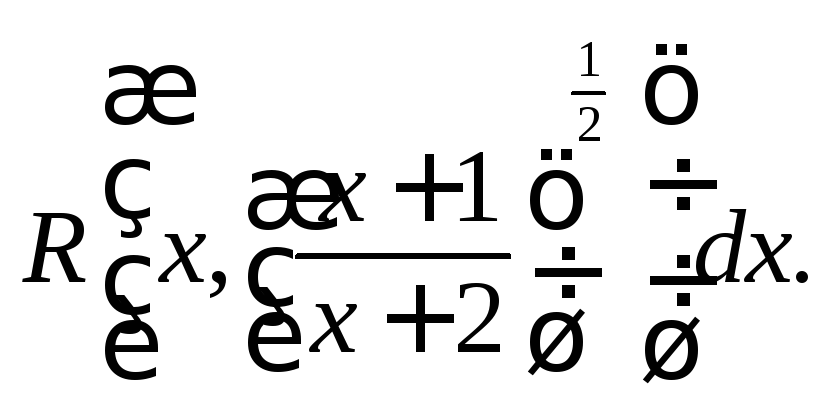
Применим
подстановку
![]()
![]()
![]()
![]()
![]()
Получаем:
![]()
4)
Интеграл имеет вид:
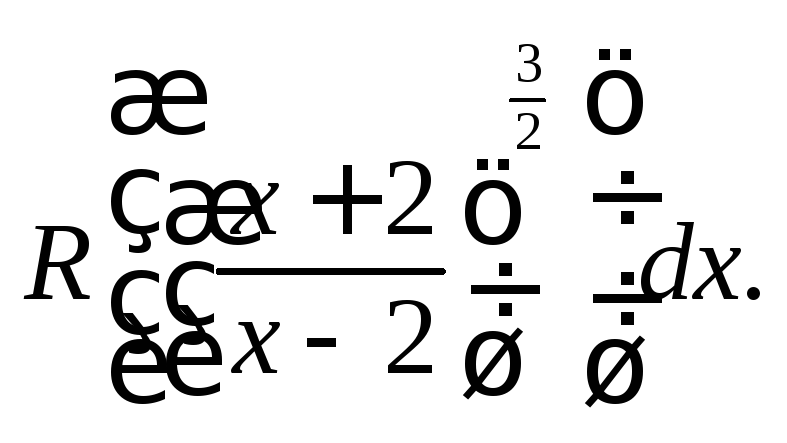
Применим
подстановку
![]()
![]()
![]()
![]()
![]()
![]()
Получаем интеграл
![]()
Для вычисления последнего интеграла вместо разложения на простейшие дроби применим формулу интегрирования по частям. Положим:
![]()
![]()
![]()
![]()
Получаем:
![]()
![]()
Заменяем
t
на
![]() тогда имеем:
тогда имеем:
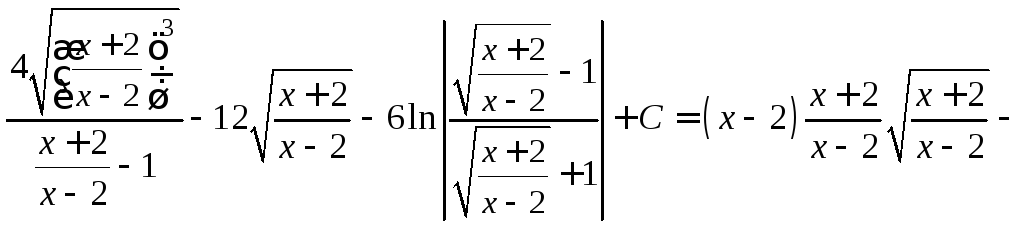
![]()
![]()
Пример 2. Найти неопределенный интеграл:
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
Решение.
1) Положим
![]()
Тогда
![]()
![]()
Интеграл примет вид:
![]()
![]()
Возвращаемся
к заданной переменной, заменяем t
на
![]() Тогда
Тогда
Приходим
к ответу:
![]()
2)
Применим подстановку
![]()
Тогда
![]()
![]()
Получаем интеграл

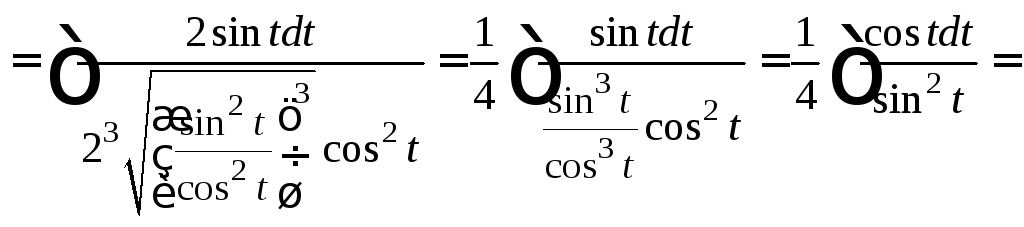
![]()
Заменяя
t
на
![]() получаем:
получаем:
![]()
Приходим
к ответу:
![]()
3)
1-й способ.
Применим подстановку
![]()
Тогда
![]()
![]()
Интеграл примет вид:

![]()

Заменяем
t
на
![]() и применяем формулу
и применяем формулу![]()
![]()
![]()
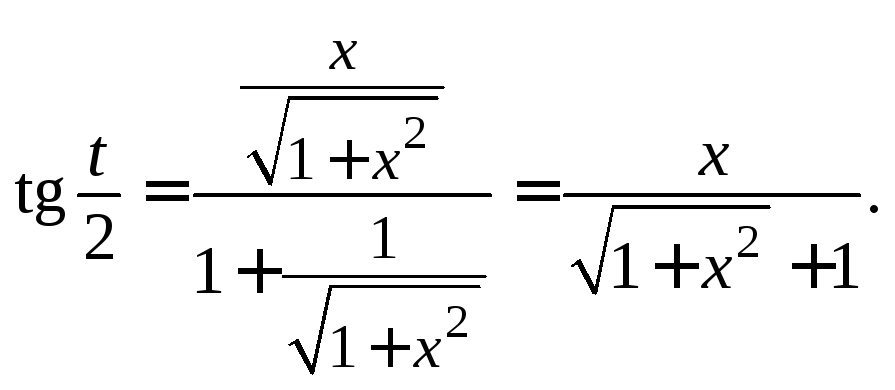
Приходим к ответу:
![]()
![]()
2-й
способ.
Применим подстановку
![]() Тогда
Тогда![]()
![]() Получаем интеграл
Получаем интеграл
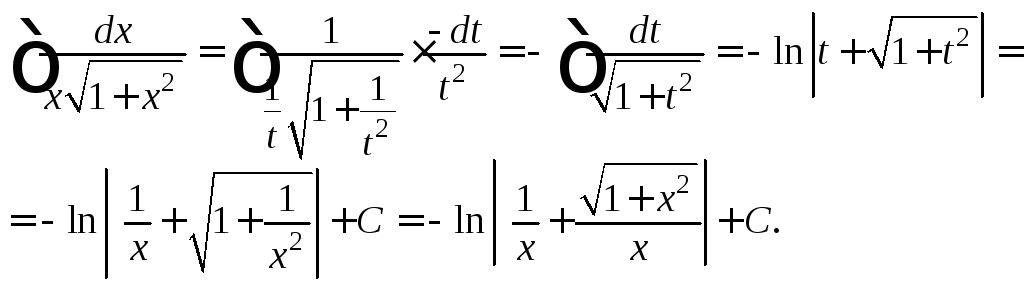
4) Выделим
полный квадрат в квадратном трехчлене
![]() Положим
Положим![]() тогда
тогда![]() получаем интеграл
получаем интеграл![]() для вычисления которого применим
тригонометрическую подстановку
для вычисления которого применим
тригонометрическую подстановку![]()
![]()
![]()
Тогда имеем:
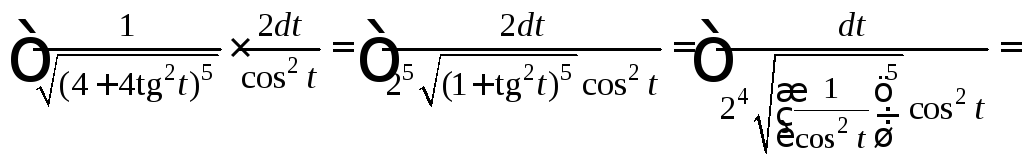
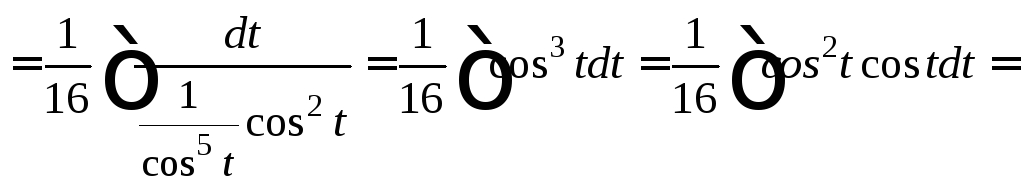
![]()
Заменяем
![]()

![]()
Приходим к ответу:
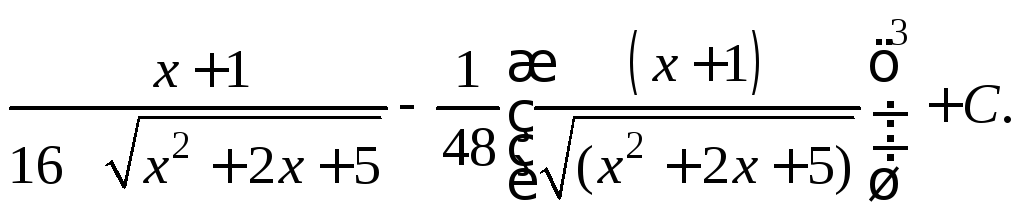
Задания
