I уровень

1.1.Найдите интеграл методом интегрирования по частям:

1) 2)3)

4) 5)6)

1.2.Найдите интеграл методом интегрирования по частям:

1) 2)

3) 4)

5) 6)

1.3.Найдите интеграл методом интегрирования по частям:

1) 2)3)

4) 5)6)

1.4.Найдите интеграл методом интегрирования по частям:

1) 2)3)

4) 5)6)

7) 8)9)

II уровень

2.1.Найдите интеграл:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

2.2.Найдите интеграл:

1) 2)3)

4) 5) 6)

7) 8)

2.3.Найдите интеграл:

1) 2)

3) 4)

2.4.Найдите интеграл:

1) 2)

3) 4)

2.5.Найдите интеграл, комбинируя методы интегрирования по частям и замены переменной:

1) 2)3)

4) 5)6)

7) 8)

III уровень

3.1.Найдите интеграл:

1) 2)3)

4) 5)6)

3.2.Получите рекуррентную формулу для вычисления интеграла и с ее помощью найдите интеграл для указанногоn:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13)

19.5. Рациональные функции. Интегрирование

простейших дробей

Рациональной функциейилирациональной дробьюназывается функция видагде– многочлены с рациональными коэффициентами степенейnиmсоответственно. Еслито дробь называетсяправильной, еслито –неправильной.

Всякую неправильную дробь путем деления числителя на знаменатель можно представить в виде суммы многочлена и правильной дроби

где – многочлены,– правильная дробь,

Интегрирование рациональных дробей сводится к интегрированию многочлена S(x) и правильной рациональной дробиЕсли выражение в знаменателе правильной дроби разлагается на множители, то ее можно представить в виде суммы простейших дробей (методы разложения на сумму простейших дробей смотрите в параграфе 2.3, часть 1, с. 47–54).

Среди правильных дробей различают четыре типа простейших дробей:

I

II

III

IV

где A,M,N,a,p,q– постоянные действительные числа,k– натуральное число, дискриминант

Неопределенные интегралы от простейших дробей

1.

2.

3. Интегрирование простейшей дроби IIIтипа производят соответственно способу вычисления интеграла (19.19), который описан в параграфе 19.3.

4. В числителе дроби IVтипа выделим производную квадратного трехчлена

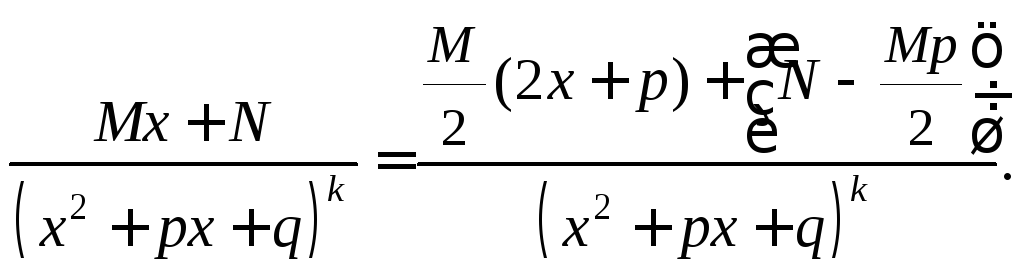
Тогда

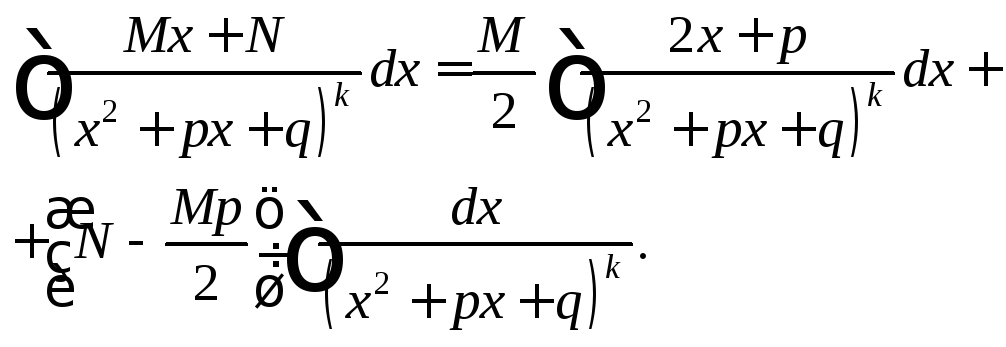
Вычислим интегралы последней суммы отдельно.

Согласно формуле (19.3) таблицы интегралов, имеем:

Для вычисления второго интеграла выделим в знаменателе полный квадрат:

Сделаем замену переменной Обозначивполучим:

Последний интеграл, который обозначим вычисляется по рекуррентной формуле

(19.21)

где

В частности,

Интегралы вида гдеm– целое положительное число, вычисляются с помощью заменыТогда

Эта замена приводит к интегралу

Пример 1. Найти интегралы:

1) 2)

3) 4)

Решение. 1) Разложим на множители знаменатель дроби:

Так как каждый множитель ивходит в знаменатель в первой степени, то каждому из них соответствует простейшая дробьI типа. Тогда общий вид разложения на сумму простейших дробей будет иметь вид:

Приведем правую часть к общему знаменателю:

Приравнивая числители, получаем:

Два многочлена равны, если равны коэффициенты при одинаковых степенях переменной x. Приравняем эти коэффициенты:

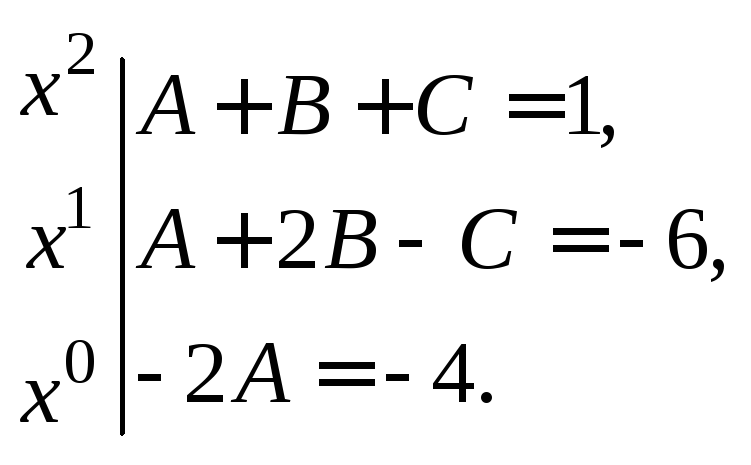
Получили систему уравнений

Решая ее, находим С = 2. Таким образом,

Значит,

2) Подынтегральная функция является неправильной дробью. Путем деления числителя на знаменатель выделим целую часть рациональной дроби и правильную рациональную дробь:

Тогда

Разложим на множители знаменатель правильной дроби:

Имеем:

откуда

Найдем коэффициенты методом частных значений. В последнем равенстве, полагая последовательно получаем соответственно:

т. е.

Следовательно,

Поэтому

3) Знаменатель подынтегрального выражения имеет корень кратности 2, и простой кореньОбщий вид разложения на простейшие дроби подынтегральной функции в данном случае будет иметь вид:

Приведем правую часть этого равенства к общему знаменателю и приравняем числители:

Приравняв коэффициенты при одинаковых степенях переменной x, получаем систему уравнений, решая которую, находим коэффициенты:

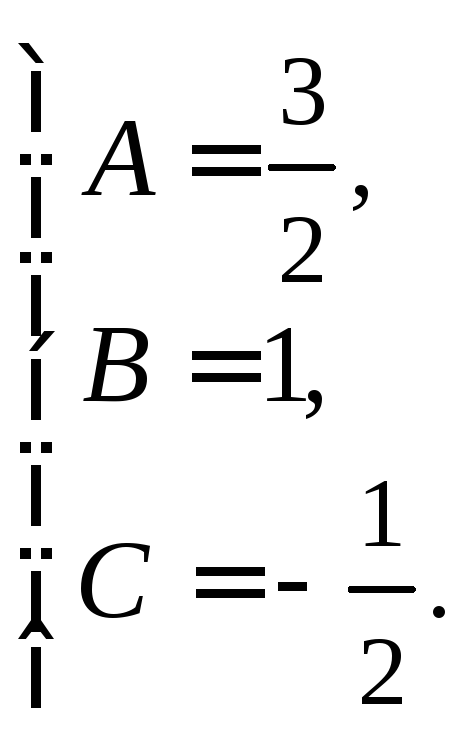
Таким образом имеем разложение:

Тогда

4) Знаменатель подынтегрального выражения имеет простой корень которому соответствует простейшая дробьI типа, и корень кратности 3, которому соответствует сумма трех простейших дробейI и II типов. Имеем:

Приведем правую часть этого равенства к общему знаменателю и приравняем числители:

Найдем коэффициенты методом частных значений. Полагая получаем:Приимеем:

Найдем производную от обеих частей последнего равенства:

Полагая получаем:Приимеем:

Таким образом,

Тогда

Пример 2. Вычислить неопределенный интеграл:

1) 2)

3) 4)

Решение. 1) Поскольку квадратный трехчлен не имеет действительных корней, то приходим к следующему общему виду разложения подынтегральной функции на простейшие дроби:

Приведение правой части к общему знаменателю и приравнивание числителей дает уравнение:

т. е.

Приравняв коэффициенты при одинаковых степенях x, получаем систему уравнений

Решая полученную систему, находим коэффициенты:

Таким образом,

Следовательно,

2) Имеем:

откуда

Для нахождения неизвестных коэффициентов применим одновременно метод частных значений и метод неопределенных коэффициентов. Подставляя находим:

Для нахождения коэффициентов B и C достаточно приравнять коэффициенты при x² и x⁰:

Из последней системы уравнений получаем:

Таким образом,

Тогда

3) Поскольку квадратные трехчлены ине имеют действительных корней, то приходим к следующему общему виду разложения подынтегральной функции на сумму простейших дробей:

Приводим правую часть этого равенства к общему знаменателю и приравниваем числители. Получаем уравнение

Приравняв коэффициенты при одинаковых степенях переменной х, получаем систему уравнений

Решая полученную систему, находим коэффициенты: Таким образом,

Следовательно,

4) В данном случае при разложении подынтегральной функции на простейшие дроби в качестве слагаемых будем иметь простейшие дроби I, III и IV типов:

Отсюда получаем:

Полагая получаем:Приведем подобные члены в правой части этого равенства:

Приравнивая коэффициенты при одинаковых степенях переменной x, получим систему уравнений

Из нее находим

Следовательно,

Тогда

Для нахождения последнего интеграла сделаем замену переменной и применим рекуррентную формулу (19.21) для случая

где

Тогда получаем:

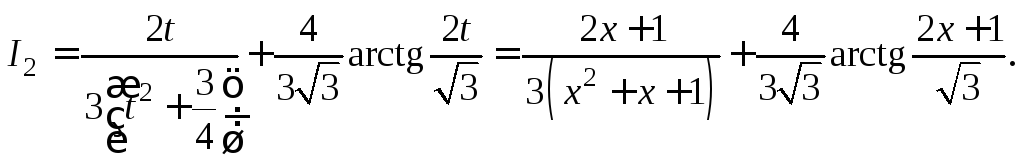
Приходим к ответу:

Пример 3. Вычислить интегралы:

1) 2)

Решение. 1) Подынтегральная функция является неправильной дробью. Выделим целую часть дроби, разделив ее числитель на знаменатель по правилу деления многочленов:

Тогда

2) Сделаем замену ТогдаПолучаем интеграл

Возвращаемся к старой переменной, подставим и получаем:

Задания