I уровень

1.1.Найдите неопределенный интеграл:

1) 2)3)

4) 5)6)

7) 8)9)

1.2.Найдите неопределенный интеграл:

1) 2) 3)

4) 5)6)

7) 8)9)

II уровень

2.1.Найдите неопределенный интеграл:

1) 2)

3) 4)

2.2.Найдите неопределенный интеграл:

1) 2)

3) 4)

III уровень

3.1.Найдите неопределенный интеграл:

1) 2)

3) 4)

19.4. Метод интегрирования по частям

Пусть функции иимеют непрерывные производныеиТогда имеет место равенство

(19.20)

Формула (19.20) задает метод интегрирования по частям, согласно которому интегрирование выраженияudvсводится к интегрированию выраженияvduПрименение формулы (19.20) предполагает, что в правой части интегралможет быть вычислен легче, чем исходный. Формула (19.20) может быть записана также в виде

Рациональность вычисления некоторых интегралов зависит от того, как выбраны функции ив заданном интеграле.

Формула интегрирования по частям может применяться неоднократно.

Рассмотрим следующие случаи:

1. Для вычисления интегралов вида где– многочлен степениn, в качестве функцииследует взять многочлена в качестве– одно из выраженийсоответственно. При этом формулу интегрирования по частям следует применятьnраз.

2. Для интегралов вида ив качестве функцииможно взятьилиФормулу интегрирования по частям следует применить дважды, а затем из полученного равенства, как из уравнения, найти заданный интеграл.

3. Для интегралов вида в качествеu(x) берут функцииlnx,а в качествеdv– выражениеТакой подход используют и тогда, когда

Во многих случаях подынтегральная функция зависит не только от аргумента, но и от натурального индекса n. Методом интегрирования по частям удается привести интеграл к интегралу такой же формы, но с меньшим значением индекса. После нескольких таких шагов приходят к интегралу, который можно вычислить с помощью таблицы. Такой метод интегрирования называютрекуррентным методом, а полученную формулу –рекуррентной формулой.

Пример 1. Методом интегрирования по частям найти неопределенный интеграл:

1) 2) 3)

Решение. 1) Положим ТогдаИспользуя формулу (19.20) интегрирования по частям, получаем:

2) Применим формулу (19.20) интегрирования по частям:

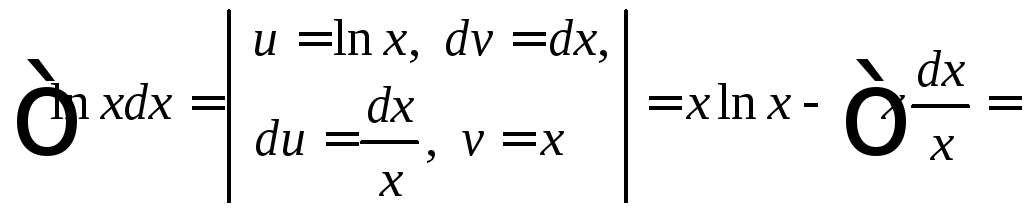
3) Положим ТогдаПрименяя формулу (19.20), получаем:

Применив формулу интегрирования по частям, понизили степень многочлена на единицу. Чтобы найти применим еще раз метод интегрирования по частям. ПоложимТогдаПолучаем:

Пример 2. Методом интегрирования по частям найти неопределенный интеграл:

1) 2)

Решение. 1) Интеграл уже был вычислен в параграфе 19.2. (см. пример 2, с. 15–16 данного пособия) методом подстановки. Рассмотрим второй способ его вычисления, используя метод интегрирования по частям:

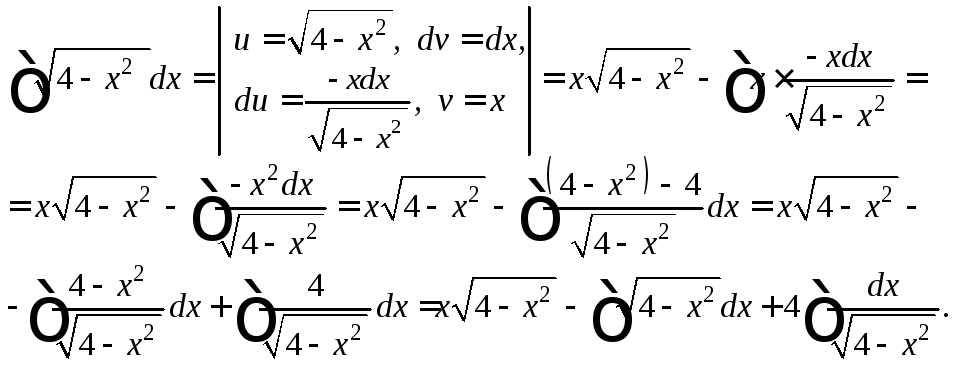
Вычислим последний интеграл, используя формулу (19.14) таблицы интегралов. Получим равенство

В правой части этого равенства получили исходный интеграл. Найдем его из уравнения: откуда получаем ответ:

2) Используя формулу интегрирования по частям дважды, получаем:

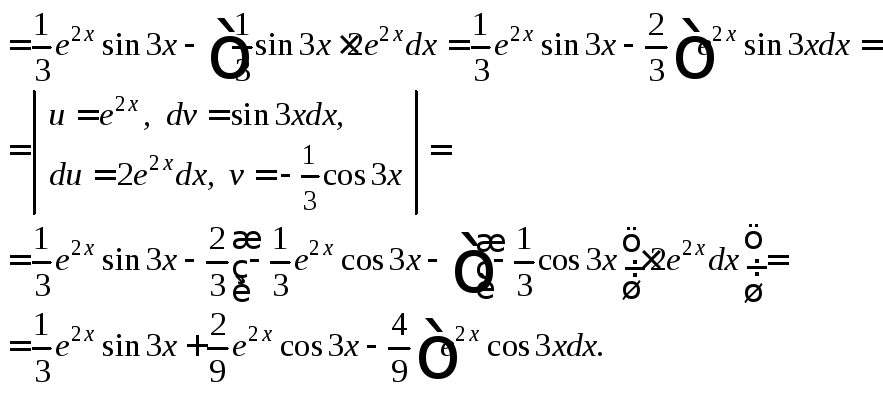
В результате получили равенство

из которого находим:

Приходим к ответу:

Пример 3. Найти неопределенный интеграл

Решение. Используя формулу (19.20) интегрирования по частям, получаем:

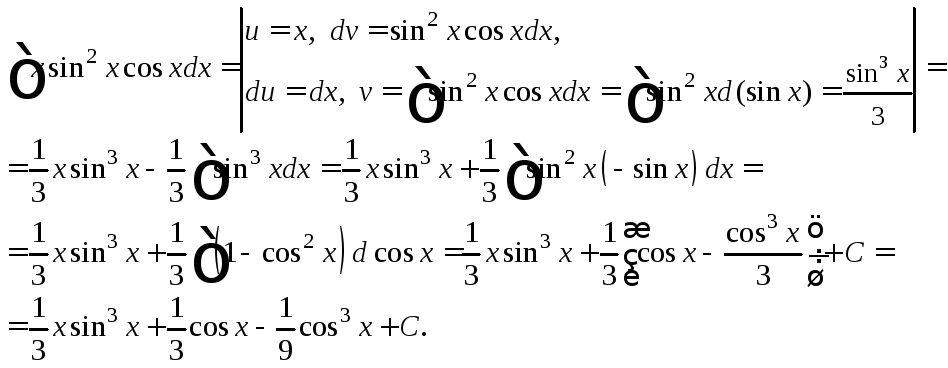
Пример 4. Найти неопределенный интеграл

Решение. Преобразуем подынтегральное выражение:

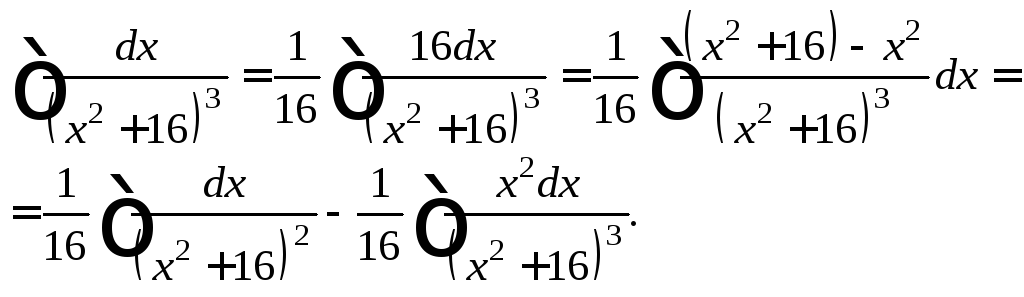
Последний интеграл вычислим, применяя формулу интегрирования по частям.

Полагаем

Если то

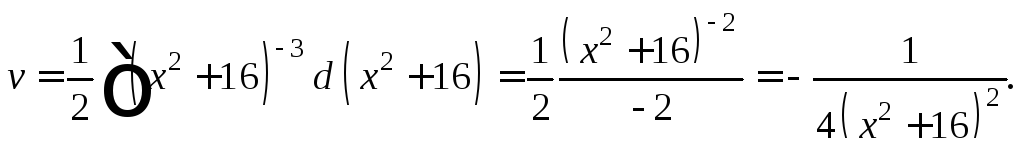
Тогда

Таким образом, получаем выражение интеграла через интеграл

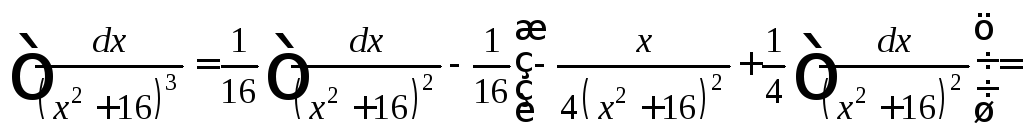
Вычисляем аналогично первоначальному.

Для вычисления последнего интеграла применяем формулу интегрирования по частям:

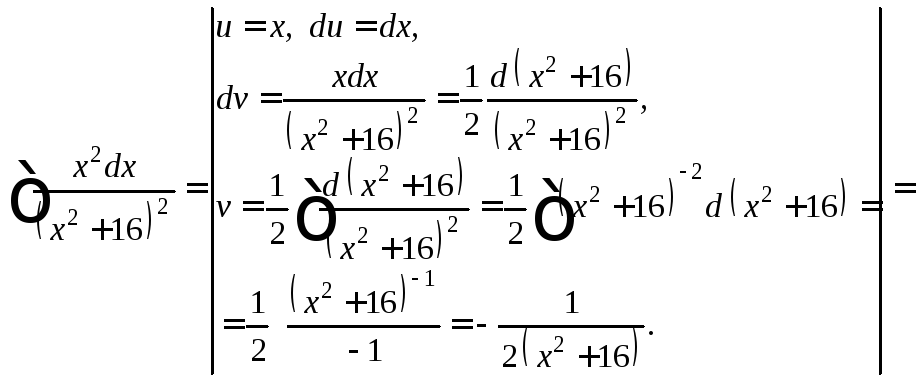
Имеем:

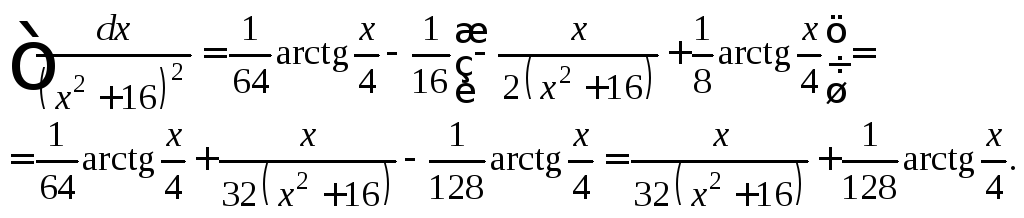
Получаем:

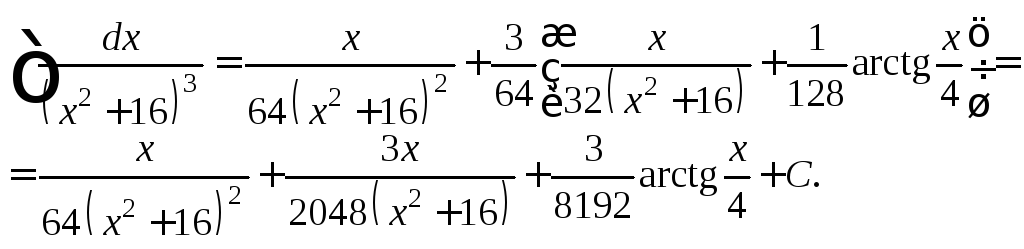
Пример 5. Получить рекуррентную формулу для вычисления интеграла Используя ее, вычислить

Решение. Обозначим

Мы получили:

Выражаем:

Это и есть рекуррентная формула, которая позволяет уменьшать показатель степени в подынтегральной функции до тех пор, пока не придем к интегралу илив зависимости от того, является лиn числом четным или нечетным.

Используем ее для вычисления

Задания