I уровень

1.1.Найдите интеграл от простейшей дроби:

1) 2)3)

4) 5)6)

7) 8)9)

10) 11)12)

1.2.Найдите интеграл от простейшей дробиIVтипа:

1) 2)3)4)

1.3.Найдите интеграл от простейших дробей:

1) 2)

3) 4)

II уровень

2.1.Найдите неопределенный интеграл:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

2.2.Найдите неопределенный интеграл:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

III уровень

3.1.Найдите неопределенный интеграл:

1) 2)

3) 4)

19.6. Интегрирование тригонометрических выражений

Для вычисления интегралов вида гдеa, b, c, d– действительные числа, применяют следующие тригонометрические формулы:

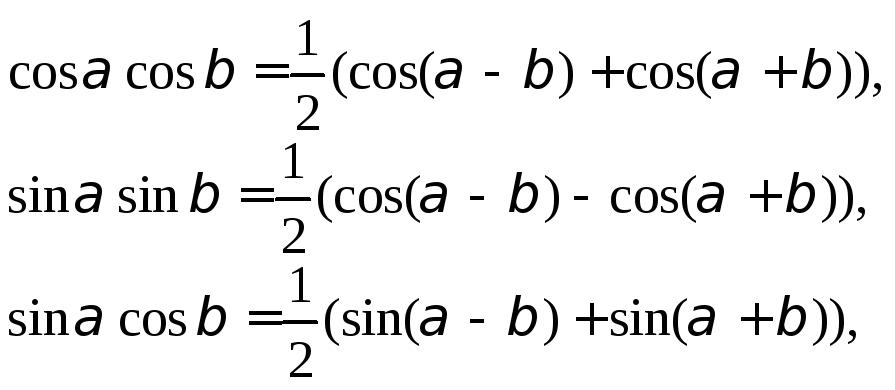(19.22)

с помощью которых произведение тригонометрических функций переводится в сумму.

Вычисление интеграла вида

(19.23)

зависит от показателей степеней mиn.

Рассмотрим следующие случаи:

1. Если в формуле (19.23) m– нечетное положительное число, т. е.то подынтегральное выражение преобразуется следующим образом:

Делают это с целью поднесения под знак дифференциала.

Тогда

Получаем интеграл от степенной функции относительно

В случае сразу имеем:

Аналогично поступают, если в формуле (19.23) n– нечетное положительное число, т. е. отдельно множительможно поднести под знак дифференциала.

2. Если в формуле (19.23) то:

1) подынтегральная функция представляет собой дробь, в числителе которой находится степень синуса, а в знаменателе – степень косинуса или наоборот (степень числителя меньше степени знаменателя), причем показатели степени или оба четные или оба нечетные;

2) подынтегральная функция представляет собой дробь, числитель которой постоянная величина, а знаменатель – произведение степеней синуса и косинуса одинаковой четности.

В этих случаях применяют подстановки иликоторые преобразуют подынтегральную функцию в степенную функцию относительноили

При этом, если применяют подстановку то используются формулы:

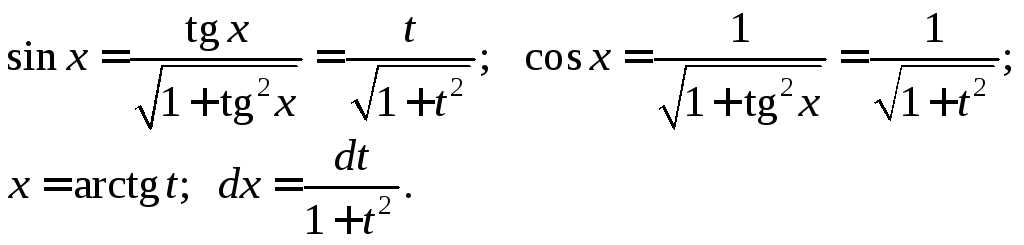(19.24)

Если применяют подстановку то используются формулы:

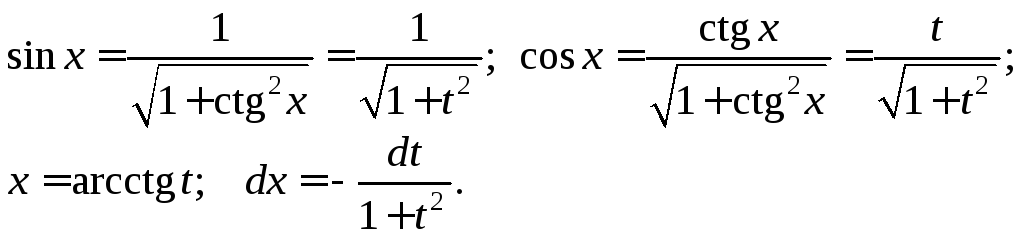(19.25)

Для дроби первого вида, если в числителе находится степень то рациональнее применить подстановкуесли в числителе находится степеньто – подстановкуВ случае, есличислаmиnмогут быть не целыми.

3. Если (m,n– целые числа), то подынтегральное выражение имеет один из видовилии тогда интеграл приводится к видуилиДля вычисления следует применить соответственно подстановкиииликоторые приводят к интеграламилисоответственно. Выполняя деление (в первом случаеделим наа во втором– на), придем к выражению, которое непосредственно интегрируется.

Для вычисления интегралов вида иможно использовать также формулы:

(19.26)

последовательно понижая степень тангенса или котангенса. С помощью формул (19.26) можно вычислять интегралы вида

где n– целое положительное число, и интегралы вида

где m,n– целые положительные числа.

4. Интегралы вида ивычисляются с помощью тригонометрических формул понижения степени:

(19.27)

Интеграл вида

(19.28)

где вычисляется с помощью формул (19.27) и формулы

(19.29)

5. Интеграл вида гдеR– рациональная функция, аргументами которой являютсяит. е. над синусом и косинусом проводятся только рациональные операции (сложение и вычитание, умножение на постоянные величины, возведение в целые степени как положительные, так и отрицательные, деление), вычисляется с помощью универсальной тригонометрической подстановкиПри этом

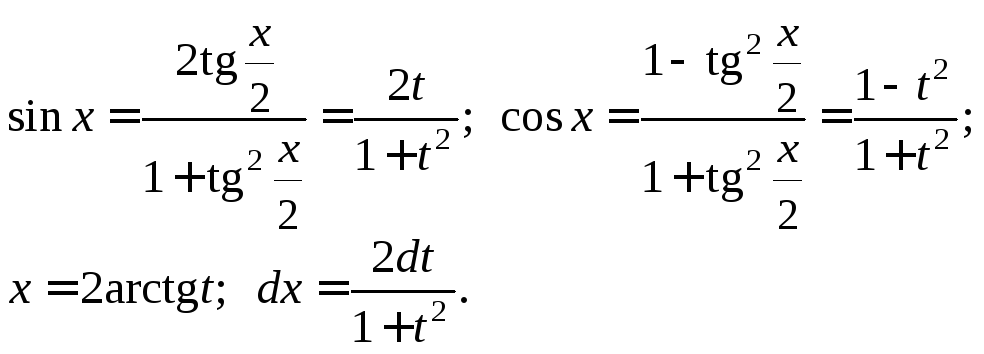(19.30)

Таким способом удобно вычислять интегралы вида а такжегде числаa,bодновременно не равны нулю.

Вместе с тем, универсальная подстановка часто приводит к громоздким вычислениям, поэтому ее следует применять в тех случаях, когда невозможно найти более удобный способ.

Частные подстановки

1. Если – нечетная функция относительнот. е.то подынтегральное выражение приводится к рациональной функции подстановкой

2. Если – нечетная функция относительнот. е.то подынтегральное выражение приводится к рациональной функции подстановкой

3. Если – четная функция относительноит. е.то подынтегральное выражение приводится к рациональной функции подстановкой

4. Интеграл приводится к рациональной функции с помощью подстановки

5. Интеграл приводится к рациональной функции с помощью подстановки

Пример 1. Найти неопределенный интеграл:

1) 2)

Решение. 1) Заменяя произведение по формуле (19.22), получаем:

2) Интеграл также можно вычислить, преобразуя произведение тригонометрических функций в сумму. Используем иной способ:

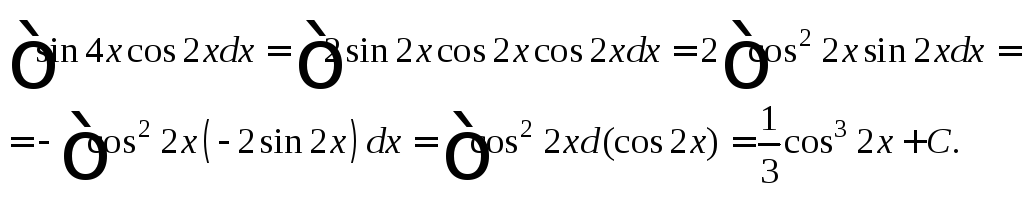
Пример 2. Найти неопределенный интеграл:

1) 2)3)

Решение. 1) Показатель степени синуса – нечетное натуральное число. Поэтому в подынтегральной функции выделим первую степень синуса:

Получаем:

Интегрируя как степенную функцию относительно получаем:

2) В подынтегральной функции выделим степень косинуса:

Получим:

Интегрируя как степенную функцию относительно получаем:

3) Поскольку то имеем:

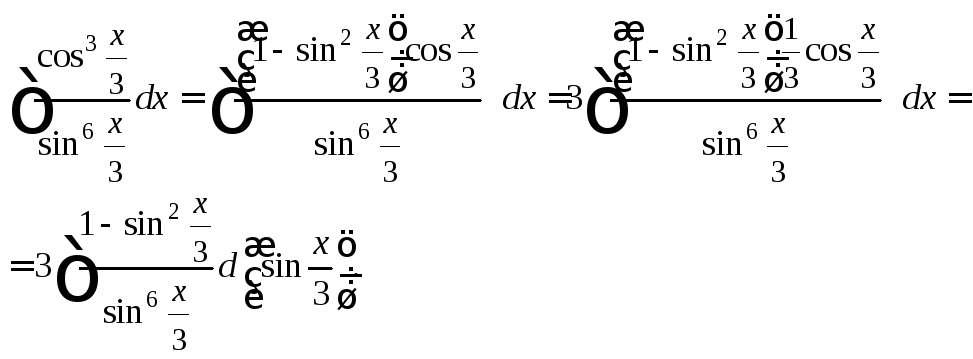
Применим подстановку

Возвращаемся к старой переменной. Заменяем t на и получаем:

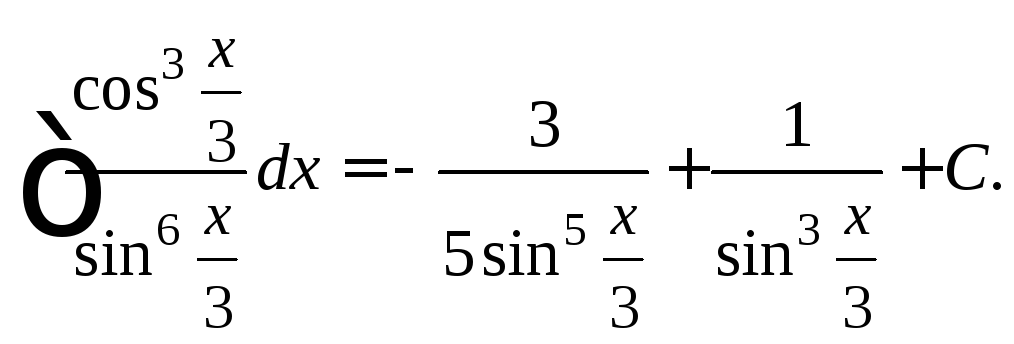
Пример 3. Найти неопределенный интеграл:

1) 2)

3) 4)

Решение. 1) Показатель степени синуса показатель степени косинуса– четное отрицательное число. Так как в числителе находится степень синуса, то применим подстановкуи используем формулы (19.24). Получаем:

Заменив t на окончательно получаем:

2) Показатель степени синуса показатель степени косинуса– четное отрицательное число. Так как в числителе находится степень косинуса, то удобнее применить подстановку

Используя формулы (19.25), получаем:

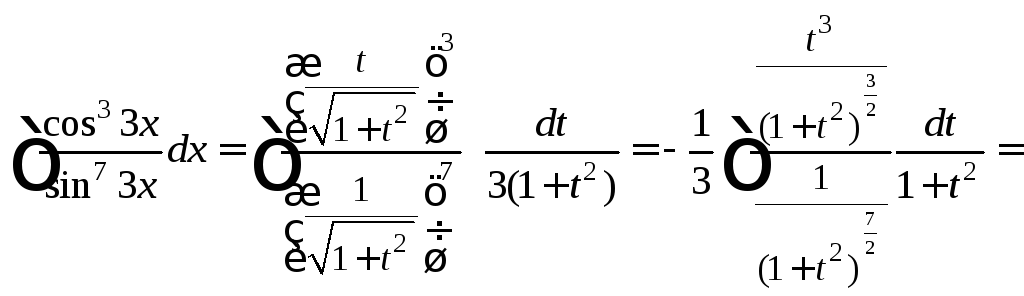
Заменив t на получаем:

3) 1-й способ. Показатель степени синуса показатель степени косинуса– четное отрицательное число. Применим подстановкутогдаИспользуя формулы (19.24), получаем:

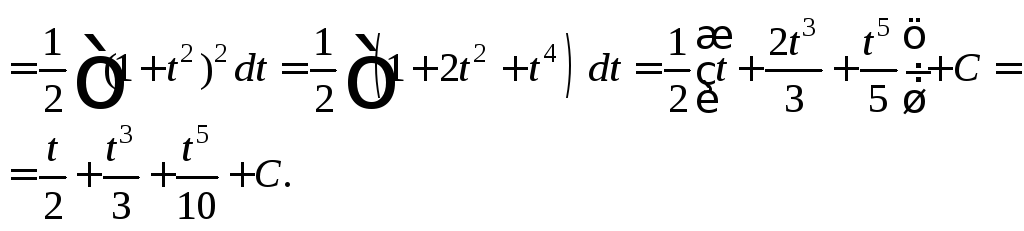
Заменяем t на и получаем:

2-й способ. Преобразуем подынтегральное выражение и применим формулы (19.26):

Интегрируя как степенную функцию относительно получаем:

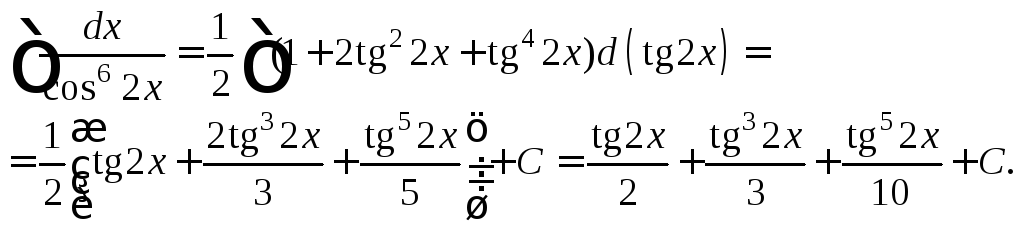
4) Имеем – четное отрицательное число. Применим подстановкуи формулы (19.24), получаем:

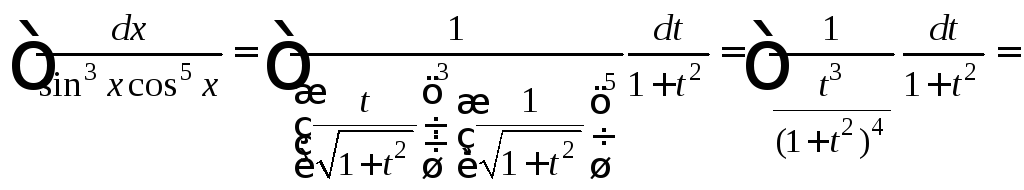
Пример 4. Найти неопределенный интеграл:

1) 2)

Решение. 1) Показатель степени синуса показатель степени косинуса– четное отрицательное число. Применив подстановкуи формулы (19.24), получаем:

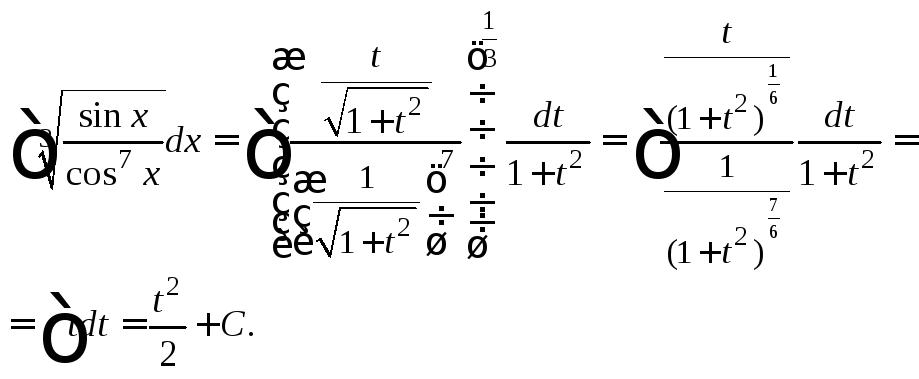
Возвращаемся к старой переменной. Заменяя t на получаем:

2) Преобразуем подынтегральную функцию к виду

Имеем – четное отрицательное число. Применив подстановкуи формулы (19.24), получаем:

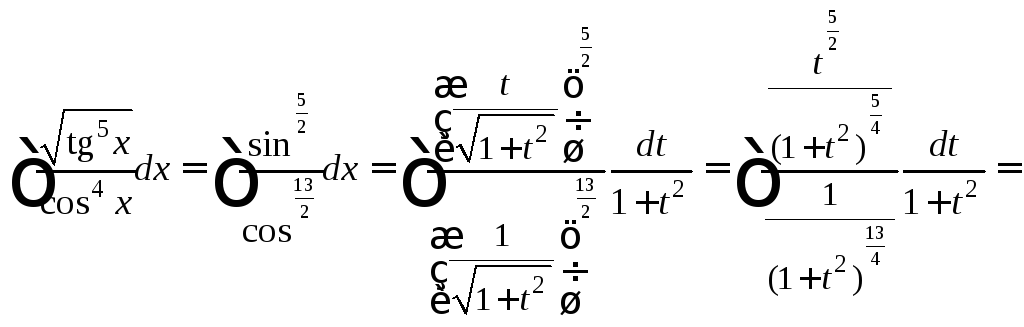
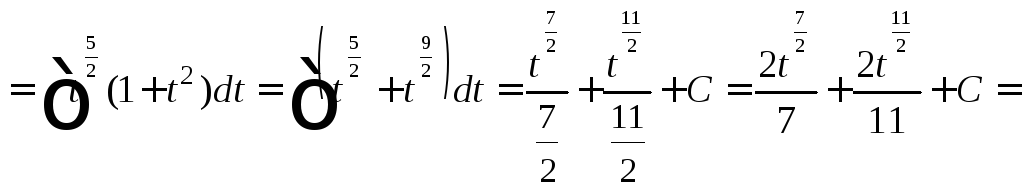
Пример 5. Найти неопределенный интеграл:

1) 2)

Решение. 1) 1-й способ. Применяя подстановку и формулы (19.24), получаем:

Заменяем t на tg x:

2-й способ. Представив подынтегральную функцию в виде и применив формулу (19.26), получаем:

Еще два раза применим формулу (19.26):

Учитывая, что получим интеграл от рациональной функции относительно

2) Имеем интеграл вида (19.23). Используя формулу (19.29), получаем:

Далее, понижая степень по формуле (19.27), имеем:

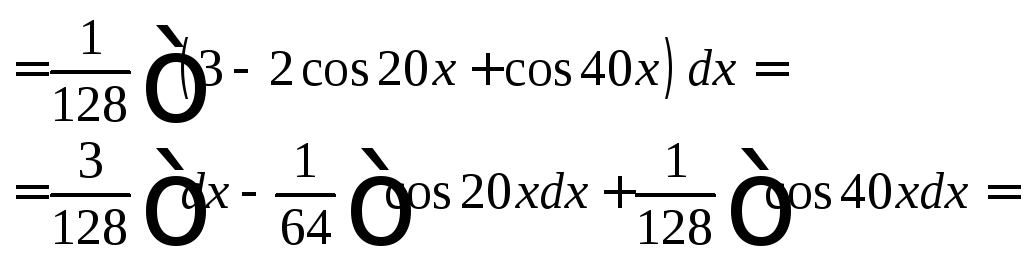
Пример 6. Найти неопределенный интеграл:

1) 2)

Решение. 1) Запишем подынтегральную функцию

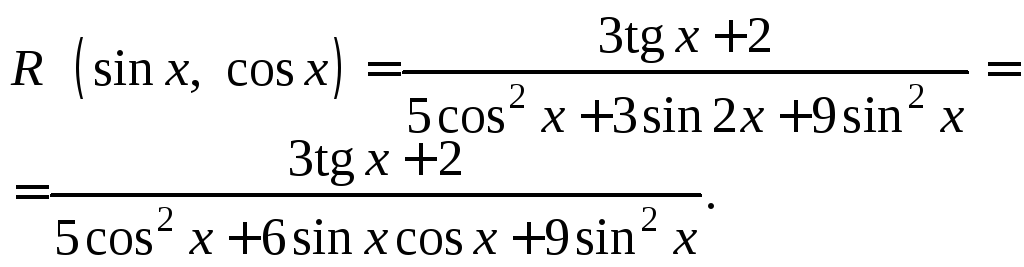
Так как подынтегральная функция является четной по sin x и cos x, т. е. то применим подстановкуВначале умножим и поделим знаменатель подынтегрального выражения наполучаем:

Возвращаемся к заданной переменной, заменяем t на tg x и приходим к ответу:

2) Поскольку подынтегральная функция не является нечетной ни по sin x, ни по cos x, то применим универсальную тригонометрическую подстановку и формулы (19.30). Получаем:

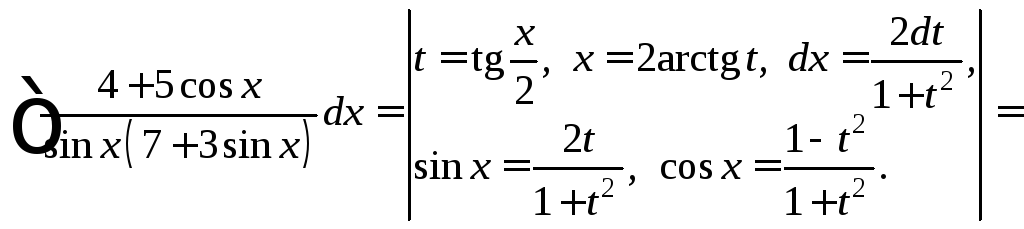
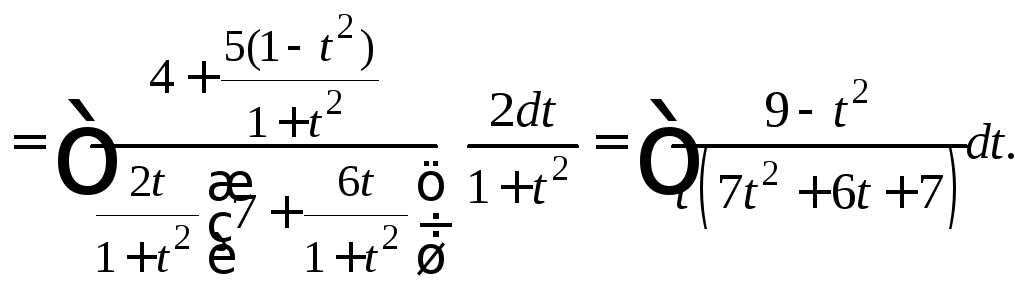
Разложив подынтегральную функцию на сумму простейших дробей, сводим заданный интеграл к разности двух интегралов, которые вычисляем:

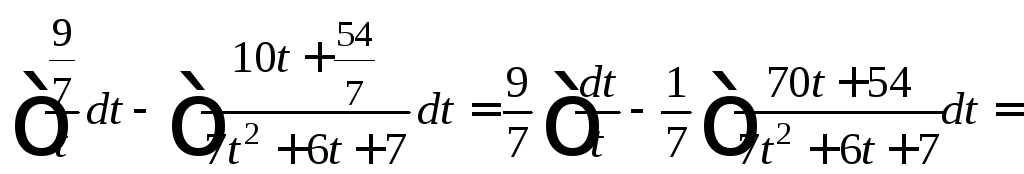
Заменяя t на приходим к ответу:

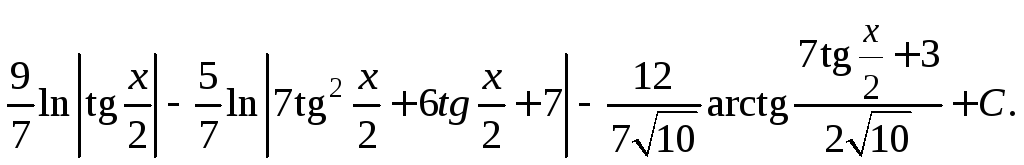
Задания