10. Записать матричное соотношение расчета периодической (циклической) дискретной функции автокорреляции последовательности Вычислить коэффициенты корреляции, построить график корреляционной функции.
11. Алгоритм «разделяй и властвуй». Вычисление полинома в точках с помощью алгоритма «разделяй и властвуй». Привести пример.
Контрольное задание № 29
1.
Оцените аддитивную, мультипликативную
и тотальную сложность вычисления
значения полинома
:
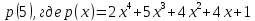– при непосредственном вычислении;
– при помощи схемы (алгоритма) Горнера.
2.
Вычислите множество значений дискретного
многочлена Чебышева
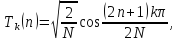для
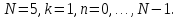
3.
Вычислить матричное произведение 𝐴𝐵,
если 𝐴
=
,
𝐵
=
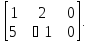
Вычислите
кронекеровское (прямое) произведение
матриц 𝐴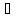
𝐵,
если 𝐴
=
,
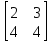𝐵
=
Вычислить значение матрицы 𝑈 = 𝑅 ∨ 𝑆.
U
=
∨
=
Вычислить значение матрицы 𝐼 = 𝑅 ∧ 𝑆.
𝐼 =
∧
=
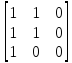Вычислить
значение матрицы 𝐷
= R
S.
𝐷 =
=
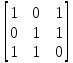4. Построить поле Галуа 𝐺𝐹(4) с помощью арифметических таблиц.
5.
Найти элемент поля Галуа обратный
элементу
,
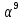если элементы поля порождаются полиномом
𝑝(𝑥)
= (1+ 𝑥+
),
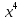неприводимым над полем 𝐺𝐹(2).
6.а.
Задана порождающая матрица 𝐺
линейного группового кода
Найти проверочную матрицу кода
6.б. Построить таблицу смежных классов этого кода.
7.а.
Используйте таблицу смежных классов
кода (п.6.б) для контроля над ошибками
(обнаружения или исправления ошибок),
если получены слова: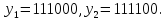
7.б.
Используйте метод синдромного
декодирования линейного группового
кода (п.6.б) для контроля над ошибками,
если получены слова:
.
8.а. Источник имеет следующие символы алфавита с их частотами появления:
|
символ |
а |
б |
с |
д |
е |
ч |
и |
|
частота |
8 |
7 |
12 |
1 |
4 |
2 |
6 |
Постройте кодовое дерево Хаффмана.
8.б. Запишите код Хаффмана.
9.
Записать матричное соотношение расчета
апериодической (линейной) дискретной
функции взаимной корреляции
последовательностей
Вычислить коэффициенты корреляции,
построить график корреляционной функции.
10.
Записать матричное соотношение расчета
периодической (циклической) дискретной
функции взаимной корреляции
последовательностей
Вычислить коэффициенты корреляции,
построить график корреляционной функции.
11. Алгоритм «разделяй и властвуй». Вычисление полинома в точках с помощью алгоритма «разделяй и властвуй». Привести пример.
Контрольное задание № 30
1.
Оцените аддитивную, мультипликативную
и тотальную сложность вычисления
значения полинома
:
– при непосредственном вычислении;
– при помощи схемы (алгоритма) Горнера.
2.
Вычислите множество значений дискретного
многочлена Чебышева
для
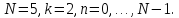
3.
Вычислить матричное произведение 𝐴𝐵,
если 𝐴
=
,
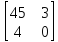𝐵
=
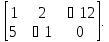
Вычислите
кронекеровское (прямое) произведение
матриц 𝐴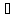
𝐵,
если 𝐴
=
,
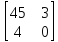𝐵
=
Вычислить значение матрицы 𝑈 = 𝑅 ∨ 𝑆.
U
=
∨
=
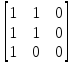Вычислить значение матрицы 𝐼 = 𝑅 ∧ 𝑆.
𝐼 =
∧
=
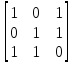Вычислить
значение матрицы 𝐷
= R
S.
𝐷 =
=
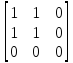
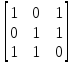4.
Задано множество целых чисел 𝐺
= {1, 2, 3, 4, 5, 6,7, 8, 9}. Найти функцию Эйлера
.
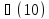5.
Привести четыре формы представления
элементов поля Галуа 𝐺𝐹(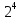
).
Поле образовано многочленами над полем
𝐺𝐺(2)
по модулю неприводимого многочлена
𝑝(𝑥)
= (1+ 𝑥
+
).
6.а.
Построить порождающую 𝐺
и проверочную
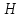матрицы линейного группового кода с
повторением с параметрами [𝑛;
1; 𝑛],
𝑛
= 10.
6.б.
Заданы n-разрядная
группа двоичных чисел
,
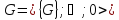𝑛
= 5 и подгруппа 𝐻
группы 𝐺
𝐻
=
.
Построить таблицу смежных классов группы 𝐺 по подгруппе 𝐻.
7.а.
Используйте таблицу смежных классов
кода (п.6.б) для контроля над ошибками
(обнаружения или исправления ошибок),
если получены слова:
7.б.
Используйте метод синдромного
декодирования линейного группового
кода (п.6.б) для контроля над ошибками,
если получены слова:
8.а. Источник имеет следующие символы алфавита с их частотами появления:
|
символ |
а |
б |
с |
д |
е |
я |
и |
|
частота |
8 |
7 |
9 |
5 |
4 |
2 |
6 |
Постройте кодовое дерево Хаффмана.
8.б. Запишите код Хаффмана.
9.
Записать матричное соотношение расчета
апериодической (линейной) дискретной
функции взаимной корреляции
последовательностей
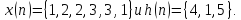Вычислить коэффициенты корреляции,
построить график корреляционной функции.
9.
Записать матричное соотношение расчета
периодической (циклической) дискретной
функции взаимной корреляции
последовательностей
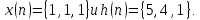Вычислить коэффициенты корреляции,
построить график корреляционной функции.
10. Алгоритм «разделяй и властвуй». Вычисление полинома в точках с помощью алгоритма «разделяй и властвуй». Привести пример.
Литература
1. Андерсон Дж. А. Дискретная математика и комбинаторика.: Пер. с англ.‒ М.: Вильямс, 2004.
2. Теория прикладного кодирования: Учеб. пособие. В 2т./ В.К. Конопелько, А.И. Митюхин и др.; Под ред. проф. В.К. Конопелько.‒ Мн.: БГУИР, 2004.
3. Митюхин, А. И., Пачинин В.И. Элементы алгебраических структур теории кодирования: учеб. пособие / А. И. Митюхин, Пачинин В. И. ‒ Минск : БГУИР, 2012.
4. Лидл Р., Нидеррайдер Г. Конечные поля: В 2т. ‒ М.: Мир, 1988.
5. Хаггарти Р. Дискретная математика для программистов. Москва: Техносфера, 2005.
6. Лосев В.В. Микропроцессорные устройства обработки информации. Алгоритмы цифровой обработки: Учеб. пособие. ‒ Мн.: Вышэйшая школа, 1990.
7. Луенбергер Д. Дж. Информатика.‒ Москва: Техносфера, 2008.
8. Вернер М. Основы кодирования. Учебник для вузов. Москва. : Техносфера, 2004.
10. Овсянников В.А. Методы формирования и цифровой обработки сигналов. Учебное пособие для студентов специальности «Радиосвязь, радиовещание и телевидение» в 2-ух частях. ‒Мн.: БГУИР 2010.
11. Ахмед Н., Рао К.Р. Ортогональные преобразования при обработке цифровых сигналов. – М.: Связь, 1980.
12. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы алгоритмы, применение. Учебное пособие. – М.: Техносфера, 2005.
13. Мак-Вильямс Ф. Дж., Слоэн Н.Дж. Теория кодов, исправляющих ошибки. – М.: Связь, 1979.
14. Касами Т., Токура Н., Ивадари Ё., Инагаки Я. Теория кодирования Пер. с яп.- М.: Мир, 1978.
15. Муттер В.М. Основы помехоустойчивой телепередачи информации. Л.: Энергоатомиздат. Ленингр. отд‒ние, 1990.
16. Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ.М.: Мир, 1986.
17. Кларк Дж., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи: Пер. с англ.-М.: Радио и связь, 1987.
18 Макклеллан Дж.К., Рейдер Ч.М. Применение теории чисел в цифровой обработке сигналов. - М.: Радио и связь, 1983.
19. Оппенгейм А., Шафер Р. Цифровая обработка сигналов.‒ М.: Техносфера, 2006.
20. Гонсалес Р., Вудс Р. Цифровая обработка изображений. ‒ М.: Техносфера, 2005.6. 22.