Шпоры / Шпоры по сопромату по 20 тем / Напряженное состояние в точке тела

3.1. Общие сведения о напряженном состоянии в точке тела

В ~ 2.5 были даны первичные понятия о напряженном состоянии в точке деформируемого тела и проведено исследование напряженного состояния для точек растянутого (сжатого) бруса. Здесь, не приводя пока никаких доказательств, рассмотрим основные положения общей теории напряженного состояния.

Напомним, что напряженное состояние в данной точке тела характеризуется совокупностью нормальных и касательных напряжений, возникающих на бесчисленном множестве различно ориентированных в пространстве площадок, которые можно провести через эту точку. Предположим, что в окрестности исследуемой точки выделен бесконечно малый элемент, имеющий форму прямоугольного параллелепипеда, и напряжения, возникающие на его гранях, известны. Каждое из этих напряжений может быть разложено на три составляющих, параллельных координатным осям. Таким образом, в общем случае на трех исходных площадках возникают девять составляющих напряжений, показанных на рис. 3.1,а (напряжения на невидимых гранях элемента не изображаем). Правило индексов для напряжений было дано на с. 22. Указанные девять величин называют компонентами напряженного состояния в данной точке.

Из условия равновесия выделенного элемента следует, что составляющие касательных напряжений, возникающих на любых двух взаимно перпендикулярных площадках, перпендикулярные общему ребру этих площадок, равны по абсолютному значению, т. е.

Это положение называют законом парности касательных напряжений. Следовательно, из девяти компонентов напряженного состояния независимы лишь шесть.

В некоторых случаях оказывается более удобным выделить элемент в виде бесконечно малой четырехгранной пирамиды (тетраэдра), как показано на рис. 3.1,б. Три грани пирамиды, совпадающие с координатными плоскостями,— это исходные площадки, а четвертую грань (площадку) проводят произвольно и возникающие на ней напряжения определяют из трех уравнений равновесия, составленных для сил, действующих на тетраэдр. Итак, первое положение теории напряженного состояния может быть сформулировано следующим образом: напряженное состояние в точке тела задано, если известны напряжения на любых трех проходящих через нее взаимно перпендикулярных площадках.

Имея зависимости, позволяющие найти напряжения по любой площадке, далее исследуют вопрос о наибольших нормальных и наибольших касательных напряжениях для рассматриваемой точки.

Среди бесчисленного множества площадок, которые можно провести через исследуемую точку, имеются три взаимно перпендикулярные площадки, касательные напряжения на которых отсутствуют. Эти площадки н возникающие на них нормальные напряжения называют главными.

Главные напряжения обозначают ; при этом индексы расставляют лишь после того, как эти напряжения вычислены, так чтобы выполнялись алгебраические неравенства

Для данной точки тела о, — наибольшее (в алгебраическом смысле), а — наименьшее напряжение. Напряжения растяжения считают положительными. О напряжении а говорят, что это промежуточное главное напряжение. В частных случаях, когда два (или все три) главных напряжения равны между собой, число главных площадок бесконечно велико. Итак, в общем случае главных площадок три, в частных случаях их бесконечно много.

Если главные напряжения в данной точке известны (заданы или определены), то наиболее удобно принять их за исходные. Классификацию видов напряженного состояния ведут по главным напряжениям.

Е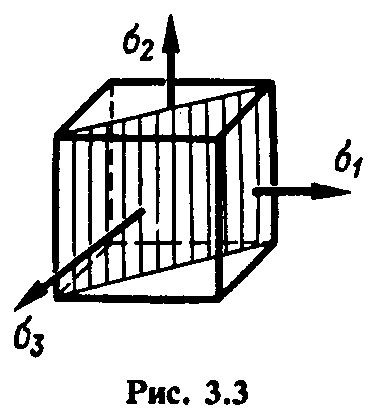сли все три главных напряжения отличны от нуля, напряженное состояние называют объемным, пространственным или трехосным. В случае если одно из главных напряжений равно нулю, напряженное состояние называют плоским или двухосным, и, наконец, если лишь одно из главных напряжений отлично от нуля, напряженное состояние линейное, или одноосное. Элементы, выделенные главными площадками, для различных частных случаев напряженного состояния показаны на рис. 3.2: а — трехосное растяжение; б — трехосное сжатие; в — трехосное смешанное напряженное состояние; г — двухосное растяжение; д — двухосное сжатие; е — частный случай двухосного смешанного напряженного состояния — чистый сдвиг; ж — одноосное растяжение; з — одноосное сжатие. Площадки, свободные от напряжений, так называемые нулевые главные площадки, покрыты точками.

Максимальное для данной точки тела касательное напряжение т „возникает на площадке, параллельной вектору и делящей пополам прямой угол между площадками действия

Это напряжение равно полуразности максимального и минимального главных напряжений.

Площадка, на которой возникает напряжение отмечена на рис. 3.3 штриховкой. На площадке, перпендикулярной отмеченной (для того чтобы не усложнять чертеж, эта вторая площадка не показана), возникает такое же по значению касательное напряжение.