
- •Минск БГУИР 2011
- •1.1. Цель и задачи преподавания дисциплины
- •1.2. Методические указания
- •1.3. Содержание дисциплины
- •1.4. Курсовая работа, ее характеристика
- •1.5. Контрольные работы, их характеристика
- •ЛИТЕРАТУРА
- •2. ЗАДАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
- •3. ВАРИАНТЫ ЗАДАНИЙ ПО КУРСОВОЙ РАБОТЕ
- •4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ ПО КУРСОВОЙ РАБОТЕ
Выполнить следующие действия:
1.Построить область допустимых значений переменных. Внутри области выбрать точку x0, которая в дальнейшем будет являться начальной в процессе поиска экстремума.
2.Найти максимальное значение функции F (x) без учета ограничений на
переменные, используя:
а) метод наискорейшего спуска; б) метод Ньютона – Рафсона.
Оптимизационный процесс начинать с выбранной точки x0.
3. Найти максимальное значение функции F (x) с учетом системы ограничений задачи, используя:
а) метод допустимых направлений Зойтендейка; б) метод линейных комбинаций; в) условия теоремы Куна – Таккера.
Оптимизационный процесс в пунктах )аи б) начинать с выбранной точки x0.
4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ ПО КУРСОВОЙ РАБОТЕ
Задание 1. Математическое описание линейных систем
Пусть
W (S )= |
Y (S ) |
= |
|
|
144S + 288 |
|
. |
(4.1) |
||
U (S ) |
S |
3 |
+ 15S |
2 |
+ 62S |
+ 48 |
||||
|
|
|
|
|
|
|||||
Передаточная функция системы W (s) – это отношение изображения по Лапласу сигнала на выходе к изображению по Лапласу сигнала на входе при нулевых начальных условиях.
Создадим стационарный линейный объект с именем w в пакете Matlab>> >> w = tf ([144 288], [1 15 62 48])
Transfer function: 144 s + 288
------------------------
s^3 + 15 s^2 + 62 s + 48
Чтобы перейти от передаточной функции к дифференциальному уравнению системы, нужно перейти из области изображений по Лапласу во временную область. Из (4.1) следует
54
Y (S) × (S3 + 15S 2 + 62S + 48) = U (S) × (144S + 288) Þ
Þ S3 ×Y (S) + 15S 2 ×Y (S) + 62S × Y (S ) + 48 ×Y (S) = 144S ×U (S) + 288 ×U (S).
Для перехода во временную область воспользуемся формальными правилами:
Y (S ) ® y(t); S × Y (S ) ® |
dy(t) |
; S 2 ×Y (S ) ® |
d 2 y(t) |
. |
|
||||||||
dt |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
dt 2 |
|
||||
Тогда дифференциальное уравнение системы имеет вид |
|
||||||||||||
|
d 3 y(t) |
+ 15 |
d 2 y(t) |
+ 62 |
dy(t) |
+ 48 y(t) = 144 |
du(t) |
+ 288u(t). |
(4.2) |
||||
|
dt3 |
dt2 |
|
|
|||||||||
|
|
|
dt |
|
dt |
|
|||||||
Характеристическое уравнение системы определяется знаменателем -пе редаточной функции:
D(S ) = S 3 + 15S 2 + 62S + 48 = 0.
Один из корней уравнения можно найти подбором, это будет l1 = 1, а затем понизить порядок уравнения и решить его:
S 3 +15S 2 + 62S + 48 S +1 |
|
S 3 + S 2 |
S 2 +14S + 48 |
14S 2 + 62S
14S 2 +14S
48S + 48
48S + 48
0
Итак, S3 + 15S 2 + 62S + 48 = (S + 1)(S 2 + 14S + 48) = 0, тогда l2 = -6,
l3 = -8, (S + 1)(S + 6)(S + 8) = 0.
В пакете Matlab корни многочлена можно найти с помощью команды pole(w).
Matlab
>> pole(w) ans =
-8.0000 -6.0000 -1.0000
55
Передаточная функция системы в форме нулей и полюсов имеет вид
|
|
|
|
|
|
|
W (S )= |
Y (S ) |
= |
|
144(S + 2) |
|
|
|
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
U (S ) |
(S +1)(S + 6)(S + 8) |
|
|
|
|
|
|
||||||||||
Получим |
разложение |
|
передаточной |
функции |
на |
|
сумму простых |
||||||||||||||||||||||
слагаемых: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
W (S ) = |
Y (S ) |
= |
|
|
|
144S + 288 |
|
= |
|
a |
|
+ |
|
|
b |
+ |
c |
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|||||||||||
|
|
|
|
|
U (S ) S 3 + 15S 2 + 62S + 48 S |
1 S |
+ 6 S + |
8 |
|
|
|||||||||||||||||||
Найдем a, b, c : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
+ |
b |
+ |
c |
= |
a(S + 6)(S + 8) + b(S +1)(S + 8) + c(S +1)(S + 6) |
= |
||||||||||||||||||||
|
S + 1 |
S + 6 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
S + 8 |
|
|
|
(S + 1)(S + 6)(S + 8) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
= |
|
|
144S + 288 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
S 3 + 15S 2 + 62S + 48 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Следовательно,
a (S + 6)(S + 8) + b(S +1)(S + 8) + c (S + 1)(S + 6) =
= a (S 2 + 14S + 48)+ b S 2(+ 9S + 8)+ c S 2(+ 7S + 6) =
= S 2 (a + b + c) + S (14a + 9b + 7c) + (48a + 8b + 6c) = 144S + 288.
Получим систему уравнений:
|
ìa + b + c = 0, |
|||||||
|
ï |
|
|
+ 7c = 144, |
||||
|
í14a + 9b |
|||||||
|
ï |
|
|
+ 6c = 288. |
||||
|
î48a + 8b |
|||||||
В |
результате решения данной |
|
системы уравнений получимa = 4,114; |
|||||
b = 57,6; |
c = -61,714. |
|
|
|
|
|
||
|
W (S) = |
4,114 |
+ |
57,6 |
- |
61,714 |
. |
|
|
|
|
|
|||||
|
|
S + 1 |
|
S + 6 S + 8 |
||||
Импульсная переходная характеристика w(t) – это процесс изменения сигнала на выходе при подаче на вход δ-функции. Ее можно найти в результате обратного преобразования Лапласа, примененного к каждому слагаемому передаточной функции.
В соответствии с таблицами соответствия |
-1 |
ì |
a |
ü |
|
-at |
|
тогда |
L |
í |
|
ý |
= ae |
|
, |
||
|
|
|||||||
|
|
îs + a þ |
|
|
|
|
||
W(t) = 4,114e-t + 57,6e-6t - 61,714e-8t .
56
Matlab
>>ch=[144 288]
>>zn=[1 15 62 48]
>>[x]=residue(ch,zn)
x =
-61.7143 57.6000 4.1143
Переходная характеристика h(t) – это процесс изменения сигнала на выходе системы при подаче на вход единичного ступенчатого воздействия. Пре-
образование по Лапласу 1(t) это |
1 |
, следовательно, |
H (S ) = |
1 |
W (S ). |
|
S |
||||
|
S |
|
|
||
Для получения аналитической формы переходной характеристики дополним систему интегратором:
W (S )= |
Y (S) |
= |
144(S + 2) |
= |
a |
+ |
b |
+ |
c |
+ |
d |
. |
|
|
|
|
|
|
|||||||
U (S) |
(S +1)(S + 6)(S + 8)S S +1 S + 6 S + 8 S |
|||||||||||
Спомощью метода неопределенных коэффициентов аналогично найдем
а= -4,114; b = -9,6; c = 7,714; d = 6.
Matlab
>>ch=[144 288]
>>zn=[1 15 62 48]
>>[c]=residue(ch,[zn,0])
c=
7.7143
-9.6000 -4.1143 6.0000
Запишем аналитическую форму переходной характеристики:
h(t ) = C1el1t + C2el2t + C3el3t + C4 , h(t) = 7,714e(-8t ) - 9, 6e(-6t ) - 4,114e(-t ) + 6.
Переходную характеристику можно также вычислить следующим обра-
t
зом: h(t )= òw(t)dt, получим такой же результат.
0
Временные характеристики системы, построенные в пакете Matlab, приведены на рис. 4.1 и 4.2.
57

График h(t)
>> step(w)
Рис. 4.1
График w(t)
>> impulse(w)
Рис. 4.2
58

Построение асимптотических ЛАХ и ФЧХ. При определении частот-
ных характеристик подразумевается, что на входе и выходе системы сигналы являются гармоническими.
|
Амплитудно-частотная характеристика (АЧХ) показывает, как изменя- |
|||||||||||||||||||||||||||||||||||
ется отношение выходного сигнала к входному в зависимости от частоты. |
|
|
|
|||||||||||||||||||||||||||||||||
|
Фазочастотная характеристика (ФЧХ) показывает изменение сдвига |
|||||||||||||||||||||||||||||||||||
фаз между входным и выходным сигналами в зависимости от частоты. |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
ЛАЧХ строится в двойных логарифмических шкалах. По одной логариф- |
|||||||||||||||||||||||||||||||||||
мической оси |
|
откладывается |
круговая |
частотаw, |
по |
|
|
|
|
|
другой |
значение |
||||||||||||||||||||||||
L(w) = 20lg K , |
выраженное в децибелах. Асимптотическая |
|
|
ЛАЧХ |
|
|
состоит из |
|||||||||||||||||||||||||||||
отрезков прямых линий с наклонами кратными 20 дБ/дек. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Преобразуем передаточную функцию к следующему виду: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
144S + 288 |
|
|
|
|
|
144(S + 2) |
|
|
|
|
|
|
|
1 |
S +1 |
|
|
|
|
|
|
|
|
||||||||
W (S )= |
|
|
|
|
= |
|
|
|
= 6 |
|
|
2 |
|
|
|
|
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
S3 +15S 2 + 62S + 48 |
(S +1)(S + 6)(S + 8) |
(S +1)( |
1 |
S |
+1)( |
1 |
S |
+1) |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
8 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Теперь она представляет собой произведение трёх апериодических и од- |
|||||||||||||||||||||||||||||||||||
ного форсирующего звена с постоянным времени T = 1; |
T = |
1 |
; T = |
1 |
; T |
= |
1 |
. |
||||||||||||||||||||||||||||
|
6 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
усиления К = 6. |
|
|
|
|
|
|
1 |
|
2 |
2 |
|
|
3 |
|
|
4 |
8 |
|
|||||||||||||
Коэффициент |
|
Сопрягающие |
частоты |
|
|
|
звеньев |
равны |
||||||||||||||||||||||||||||
w = |
1 |
= 1; w |
2 |
= |
1 |
= 2; w |
3 |
= |
1 |
= 6; w |
4 |
= |
1 |
|
= 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
T1 |
|
T2 |
|
|
T3 |
|
|
T4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
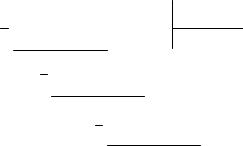
Далее необходимо правильно разметить оси, и отметить на оси w сопрягающие частоты. ЛАЧХ приведена на рис. 4.3, а.
Так как интегрирующие звенья отсутствуют, то первый наклон в области низких частот будет нулевой. Он идёт параллельно оси частот на уровне 20 lgK до первой сопрягающей частоты w1. Эта частота относится к апериодическому звену. Следовательно, наклон изменится на -1. Этот наклон будет идти
до сопрягающей частоты w2. Так как эта частота относится к форсирующему звену, то наклон изменится на +1 и станет нулевым, ЛАЧХ параллельна оси частот. После частоты w3 наклон изменится на (-1) и будет продолжаться до w4. После частоты w4 он изменится ещё на (-1) и станет равным (-2). Частота, при которой частотная характеристика пересечёт ось частот, называется частотой
среза, wср = 12 рад/с.
Фазочастотная характеристика (рис. 4.3, б) построена в соответствии с выражением
j(w) = arctg 1 w - arctgw - arctg 1 w - arctg 1 w . 2 6 8
59
Значения каждого из слагаемых определяются приближенно для значений
w ® 0 , |
w ® ¥, w i |
= |
1 |
. В этих точках |
arctg0 = 0; arctg¥ = |
p |
; |
||
|
|
||||||||
|
|
p |
|
|
Ti |
2 |
|
||
arctgw T |
= arctg1 = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
i i |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
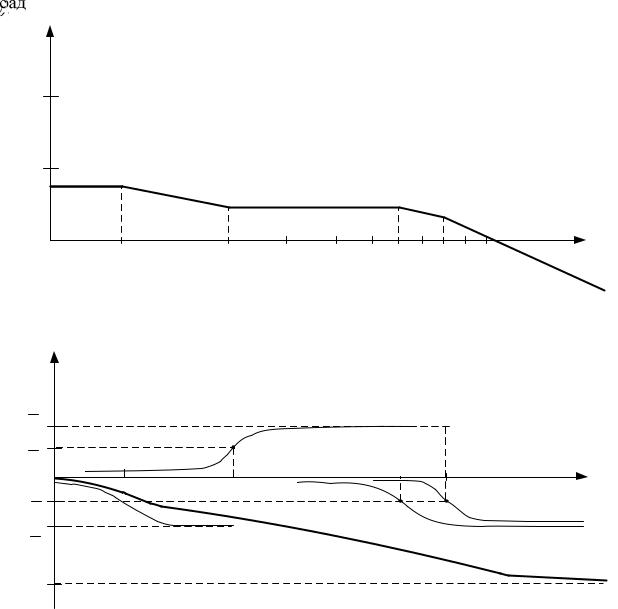
В пакете Matlab для построения ЛАЧХ и ЛФЧХ используется команда bode(w), а для построения АФЧХ командаnyquist(w). Соответствующие характеристики приведены на рис. 4.4 и 4.5.
а
p
2 p
4
- p
4
- p
2
б
Рис. 4.3
60
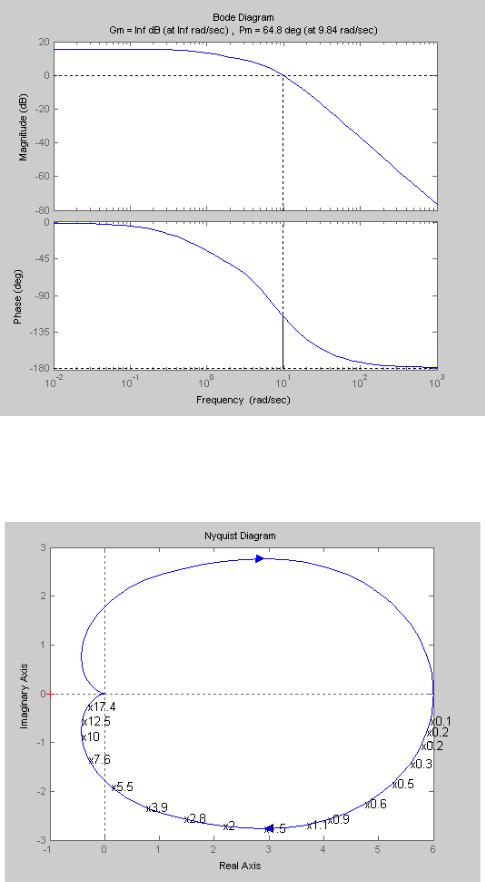
>>margin(w)
Рис. 4.4
АФЧХ системы: >> nyquist(w)
Рис. 4.5
61
Кроме входных и выходных переменных при описании систем выделяют переменные x, связанные с внутренней структурой устройства, – переменные состояния. Тогда систему можно описать с помощью уравнений состояния.
Нормальная форма уравнений состояния имеет вид
ìx& = Ax + Bu |
(4.3) |
í |
|
îy = Cx + Du |
|
Здесь А – квадратная матрица определенного вида, размер которой определяется порядком дифференциального уравнения. Элементы, стоящие над главной диагональю – единицы, элементы нижней строки – коэффициенты левой части дифференциального уравнения, взятые с противоположным знаком. Все остальные элементы – нули. Такая матрица называется матрицей Фробениуса.
Согласно (4.2) дифференциальное уравнение системы имеет вид
&&&y (t ) +15&&y (t ) + 62 y&(t ) + 48 y (t ) = 144u&(t ) + 288u(t)
a3 |
a2 |
a1 |
|
a0 |
|
|
b1 |
b0 , |
|||
где ai и bj – коэффициенты уравнения. |
|
|
|
|
|
|
|||||
|
é |
0 |
1 |
0 |
ù |
|
é |
0 |
1 |
0 |
ù |
A = |
ê |
0 |
0 |
1 |
ú |
= |
ê |
0 |
0 |
1 |
ú |
ê |
ú |
ê |
ú . |
||||||||
|
ê |
-a0 |
-a1 |
|
ú |
|
ê |
-48 |
-62 |
|
ú |
|
ë |
-a2 û |
|
ë |
-15û |
||||||
Элементы матриц B и D вычисляются по следующим рекуррентным со- |
|||||||||||
отношениям: D = b0 |
= b3 |
= 0, |
|
|
|
|
|
|
|
|
|
b1 = b 2 - a 2 b0 = 0 - 1 5 × 0 = 0,
b2 = b1 - a 2 b1 - a1b0 = 1 4 4 - 1 5 × 0 - 6 2 × 0 = 1 4 4,
b3 = b0 - a 2b2 - a1b1 - a 0b0 = 28 8 - 1 5 × 1 44 - 6 2 × 0 - 48 × 0 = -1 8 72,
|
é b |
ù |
|
|
é |
0 |
ù |
|
|
B = |
ê 1 |
ú |
, B |
= |
ê |
1 4 4 |
ú |
, C |
= [1 0 0 ]. |
êb2 ú |
ê |
ú |
|||||||
|
ê |
ú |
|
|
ê |
- 1 8 7 2 |
ú |
|
|
|
ë b3 |
û |
|
|
ë |
û |
|
|
|
62

Подставив рассчитанные матрицы в систему (4.3), получим
ìé x&1 |
ù é 0 |
1 |
0 ù |
|
é x1 |
ù |
|
é 0 |
ù |
|
|
ïêx& |
ú |
= ê 0 |
0 |
1 ú |
× |
êx |
ú |
+ |
ê 144 |
ú |
×u |
ïê 2 |
ú ê |
-62 |
ú |
|
ê 2 |
ú |
|
ê |
ú |
|
|
ïêx& |
ú |
ê-48 |
-15ú |
|
êx |
ú |
|
ê-1872ú |
|
||
ïë 3 |
û |
ë |
|
û |
|
ë 3 |
û |
|
ë |
û |
Þ |
í |
|
|
é x1 ù |
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
ï |
[ |
|
|
] |
ê 2 |
ú |
[ |
0 |
] |
|
ïy = |
1 0 0 |
|
êx |
ú + |
|
u, |
|
|||
ï |
|
|
|
|
êx ú |
|
|
|
|
|
|
|
|
|
ë 3 û |
|
|
|
|
||
î |
|
|
|
|
|
|
|
|
||
ìx&1 = x2 , |
|
|
|
|
|
|
|
|
||
ïx& |
= x |
+144u, |
|
|
|
|
||||
ï |
2 |
3 |
|
|
|
|
|
|
|
|
íx& |
= -48x |
|
- 62x |
-15x |
-1872u, |
|||||
ï |
3 |
|
1 |
|
2 |
|
|
3 |
|
|
ïy |
= x . |
|
|
|
|
|
|
|
|
|
î |
|
1 |
|
|
|
|
|
|
|
|
Схема модели приведена на рис. 4.6.
Рис. 4.6
Запишем уравнения состояния в канонической форме. Для этого введем новую переменную состояния q, которая связана с переменной состояния x следующим образом: х = М q. М – это модальная матрица, которая имеет вид
63
|
é 1 |
1 |
1 ù |
|
é 1 |
1 |
1 ù |
|
||||||
M = |
êl |
l |
2 |
l |
3 |
ú |
= |
ê-1 -6 -8ú |
, |
|||||
|
ê |
1 |
|
|
ú |
|
ê |
1 |
36 |
64 |
ú |
|
||
|
ê |
2 |
l |
2 |
|
2 |
ú |
|
ê |
ú |
|
|||
|
ël1 |
2 |
l3 |
û |
|
ë |
|
|
|
û |
|
|||
где li – характеристические числа матрицы Фробениуса А.
При подстановке q вместо x в нормальную форму уравнений (4.3) получим уравнения состояния системы в канонической форме:
ìq& = Lq + B1u,
í
îy = C1q + D1u.
Здесь L – диагональная матрица:
состояния
(4.4)
|
él1 |
0 |
0 ù |
|
é-1 0 |
0 ù |
|
|
|
||||||
L = |
ê |
0 |
l |
2 |
0 |
ú |
= |
ê |
0 |
-6 |
0 |
ú |
, B |
= M -1B, C |
= CM , D = D, |
|
ê |
|
|
|
ú |
|
ê |
|
|
|
ú |
1 |
1 |
1 |
|
|
ê |
0 |
0 |
|
ú |
|
ê |
0 |
0 |
|
ú |
|
|
|
|
|
ë |
l3 û |
|
ë |
-8û |
|
|
|
|||||||
где M-1 – матрица, обратная модальной, определяемая выражением
M -1 = |
1 |
× AdjM . |
|
||
|
det M |
|
Здесь AdjM – матрица, присоединённая к M, т. е. транспонированная матрица алгебраических дополнений.
|
|
|
|
é1,371 |
0, 4 |
0,029ù |
|
|
|
|
|
|
|
|
||
|
M |
-1 |
= |
ê |
- 0,9 |
- 0,1 |
ú |
, |
|
|
|
|
|
|
|
|
|
|
ê-0,8 |
ú |
|
|
|
|
|
|
|
||||||
|
|
|
|
ê0, 429 |
0,5 |
0,071 |
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
û |
|
|
|
|
|
|
|
|
|
é1,371 |
0, 4 |
0,029ù é |
0 |
|
|
ù |
|
é |
4,11 |
ù |
|
||||
B = M -1B = |
ê -0,8 |
-0,9 |
-0,1 |
ú ê |
144 |
|
ú |
= |
ê |
57,6 |
ú |
, |
||||
1 |
ê |
|
|
0,5 |
|
ú ê |
-1872 |
ú |
|
ê |
|
ú |
|
|||
|
ê0, 429 |
0,071ú ê |
ú |
|
ê |
-61,71ú |
|
|||||||||
|
ë |
|
|
|
|
û ë |
|
|
|
|
û |
|
ë |
|
û |
|
|
|
|
|
é 1 |
1 |
1 ù |
|
|
|
|
|
|
|
|
|
|
C = CM = [1 0 0]ê-1 -6 -8ú |
= |
[1 1 1], |
|
|
||||||||||||
1 |
|
|
|
ê |
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
36 |
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
ë 1 |
64û |
|
|
|
|
|
|
|
|
|
||
D1 = D = [0].
64
Matlab
>> M=[1 1 1;-1 -6 -8; 1 36 64]
M = |
|
|
1 |
1 |
1 |
-1 |
-6 |
-8 |
1 |
36 |
64 |
inv(M)
ans =
1.3714 0.4000 0.0286 -0.8000 -0.9000 -0.1000 0.4286 0.5000 0.0714
B=[0;144;-1872]
B =
0
144 -1872
M-1*B
ans =
4.1143
57.6000 -61.7143
Подставив найденные значения в (4.4), получим
ìéq&1 ù |
|
é-1 |
0 |
0 ù |
|
éq1 |
ù |
|
é |
4,11 |
ù |
|
||
ïêq& |
ú |
= |
ê |
0 |
-6 |
0 ú |
× |
êq |
ú |
+ |
ê |
57,6 |
ú |
×u, |
ïê 2 |
ú |
|
ê |
0 |
0 |
ú |
|
ê 2 |
ú |
|
ê |
|
ú |
|
ïêq& |
ú |
|
ê |
-8ú |
|
êq |
ú |
|
ê-61,71ú |
|
||||
ïë 3 |
û |
|
ë |
|
|
û |
|
ë 3 |
û |
|
ë |
|
û |
|
í |
|
|
|
|
éq1 ù |
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
[ |
] |
ê |
|
2 |
ú |
+ |
[ |
0 |
] |
|
|
ïy = |
1 1 1 |
êq |
|
ú |
|
u, |
|
|
||||
ï |
|
|
êq |
ú |
|
|
|
|
|
|
||
î |
|
|
ë |
|
3 |
û |
|
|
|
|
|
|
|
ìq&1 = -q1 - 4,11u, |
|||||||||||
|
ïq& |
|
= -6q |
+ 57,6u, |
||||||||
|
ï |
2 |
|
|
|
|
2 |
|
|
|
||
|
íq& |
|
= -8q |
- 61,71u, |
||||||||
|
ï |
3 |
|
|
|
|
3 |
|
|
|
||
|
ïy |
= q |
+ q |
+ q |
3 |
. |
||||||
|
î |
|
|
|
|
1 |
|
|
2 |
|
|
|
65

Схема модели, соответствующая полученной системе, приведена на рис. 4.7. Для нее характерно параллельное соединение интеграторов, выходы которых определяются переменными состояния q1, q2, q3.
Найдем решение y(t) для системы уравнений в нормальной форме, если начальные условия имеют вид y (0) = 2, y&(0) = &&y (0) = 0. Сигнал u (t ) = 2 ×1(t ). Переходя к начальным условиям для х, в соответствии с принятыми ранее обо-
значениями, получим x1 (0) = 2, x2 (0) = 0, x3 (0) = 0. |
|
|
|
|
|
||||||||||||||||||
|
Решение уравнения состояния x& = Ax + Bu |
складывается из двух состав- |
|||||||||||||||||||||
ляющих x(t) = x1(t) + x2 (t) – свободной и вынужденной. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
q&1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
4,11 |
|
|
|
|
+ ∑ |
|
|
ò |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q&2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
q2 |
|
|
|
|
|
|
||||
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
y |
|
|||||
|
|
57,6 |
|
|
|
|
+ ∑ |
|
|
|
|
ò |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ∑ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q&3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
61,71 |
|
|
|
|
- ∑ |
|
|
ò |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.7 |
|
|
|
|
|
|
|
|
|
|
||||
|
Свободная составляющая x1(t) |
|
– это общее решение дифференциального |
||||||||||||||||||||
уравнения системы с нулевой правой частью. Оно не зависит от внешнего воздействия и характеризует естественное поведение системы.
Вынужденная составляющая x2 (t) – это частное решение дифференциального уравнения с ненулевой правой частью. Оно зависит от сигнала u(t) и характеризует поведение системы под его воздействием.
Решение уравнения состояния x& = Ax + Bu имеет вид
t
x(t) = x0eA(t -t0 ) + òB × u(t) × eA(t -t)dt,
0
где e At – фундаментальная матрица или матрица перехода.
66
Она вычисляется по следующей формуле:
e At = g0 E + g1 A + g2 A2 ,
где g0, g1, g2 – неизвестные коэффициенты.
Вычислить их можно, решая матричное уравнение
é1 l l2 |
ù |
ég0 |
ù |
éel1t ù |
||||||
ê |
|
1 |
1 |
ú |
ê |
|
ú |
|||
ê1 l |
2 |
l2 |
ú × |
êg |
ú |
= êel2t ú . |
||||
ê |
|
2 |
ú |
ê |
1 |
ú |
ê |
|
ú |
|
l3 |
2 |
êg |
2 |
ú |
l3t |
|||||
ê1 |
l3 |
ú |
ë |
û |
êe |
|
ú |
|||
ë |
|
|
|
û |
|
|
|
ë |
|
û |
Для рассматриваемого примера
é1 -1 1 ù |
|
ég |
ù |
é e-t |
ù |
|||
ê |
-6 |
ú |
× |
ê |
0 ú |
ê |
-6t |
ú |
ê1 |
36ú |
ê g1 ú |
= êe |
|
ú . |
|||
ê1 |
-8 |
64ú |
|
êg |
ú |
ê |
-8t |
ú |
ë |
|
û |
|
ë |
2 û |
êe |
|
ú |
|
|
|
|
|
|
ë |
|
û |
Перемножая матрицы, получаем систему уравнений следующего вида
ìïg0 - g1 + g2 = e-t , ïíg0 - 6g1 + 36g2 = e-6t ,
ïïîg0 - 8g1 + 64g2 = e-8t .
Решение данной системы уравнений имеет вид
|
|
ìg |
0 |
= 1,371e-t - 0,8e-6t |
+ 0, 429e-8t , |
|
|
||||||
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
= 0, 4e-t - 0,9e-6t |
+ 0,5e-8t , |
|
|
|
|||||
|
|
íg1 |
|
|
|
||||||||
|
|
ï |
|
= 0, 029e-t |
- 0,1e-6t + 0,071e-8t . |
|
|
||||||
|
|
ïg |
2 |
|
|
||||||||
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
é |
0 |
|
1 |
0 |
ù |
|
|
|
é 0 |
0 |
1 |
ù |
A = |
ê |
0 |
|
0 |
1 |
ú |
Þ A |
2 |
= |
ê |
-62 |
|
ú |
ê |
|
ú |
|
ê-48 |
-15ú . |
||||||||
|
ê |
-48 |
|
-62 |
-15ú |
|
|
|
ê720 |
882 |
163 |
ú |
|
|
ë |
|
|
|
|
û |
|
|
|
ë |
|
|
û |
67
Итак,
|
|
|
|
|
é1,371 |
0 |
|
0 |
ù |
|
|
|
é-0,8 |
0 |
|
|
0 |
ù |
|
|
|
||||
e |
At |
|
= |
ê |
0 |
|
1,371 |
0 |
ú |
-t |
|
ê |
0 |
-0,8 |
|
0 |
ú |
-6t |
+ |
||||||
|
|
|
ê |
|
úe |
|
|
+ ê |
|
úe |
|
|
|||||||||||||
|
|
|
|
|
ê |
0 |
|
0 |
|
|
ú |
|
|
|
ê |
0 |
0 |
|
|
|
ú |
|
|
|
|
|
|
|
|
|
ë |
|
1,371û |
|
|
|
ë |
|
-0,8û |
|
|
|
|||||||||
|
|
é0, 429 |
|
0 |
0 |
|
ù |
|
|
|
é |
0 |
0, 4 |
|
0 ù |
|
|
|
|||||||
+ |
ê |
0 |
|
0, 429 |
0 |
|
ú |
-8t |
|
ê |
0 |
0 |
|
|
|
ú |
|
-t |
+ |
||||||
ê |
|
|
úe |
|
|
+ ê |
|
|
0, 4úe |
|
|||||||||||||||
|
|
ê |
0 |
|
|
0 |
|
|
ú |
|
|
|
ê |
|
|
|
|
|
ú |
|
|
|
|||
|
|
ë |
|
|
0, 429û |
|
|
|
ë-19, 2 -24,8 |
-6 û |
|
|
|
||||||||||||
|
|
|
|
é |
|
0 |
|
-0,9 |
0 |
ù |
|
|
|
é |
0 |
|
0,5 |
|
0 |
ù |
|
|
|
|
|
|
|
|
|
+ ê |
|
0 |
|
0 |
-0,9úe-6t |
|
+ |
ê |
0 |
|
0 |
0,5 |
úe-8t |
+ |
|
||||||
|
|
|
|
ê |
|
|
|
|
|
ú |
|
|
|
ê |
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
ê |
43, 2 |
55,8 |
|
ú |
|
|
|
ê |
-24 |
-31 |
|
|
ú |
|
|
|
|
||||
|
|
|
|
ë |
13,5 û |
|
|
|
ë |
-7,5û |
|
|
|
|
|||||||||||
|
|
é |
|
0 |
|
|
|
0 |
0,029ù |
|
|
|
é |
0 |
|
0 |
|
-0,1 ù |
|
|
|
||||
+ |
ê |
-1, 4 |
|
-1, 798 |
-0, 44úe-t |
+ |
ê |
4,8 |
6, 2 |
|
1,5 |
úe-6t |
+ |
||||||||||||
|
|
ê |
20,9 |
|
25,578 |
4,727 |
ú |
|
|
|
ê |
|
|
-88, 2 |
|
|
|
ú |
|
|
|
||||
|
|
ê |
|
ú |
|
|
|
ê-72 |
|
-16,3ú |
|
|
|
||||||||||||
|
|
ë |
|
|
|
|
|
|
|
|
û |
|
|
|
ë |
|
|
|
|
|
|
û |
|
|
|
|
é |
0 |
0 |
0,071ù |
|
|
é 1,371 |
0, 4 |
0,029 ù |
|
|
|||
+ |
ê |
|
-4, 402 |
|
ú |
-8t |
= |
ê |
|
-0, 427 |
|
ú |
-t |
+ |
ê-3, 41 |
-1, 06úe |
|
ê-1,392 |
-0,035úe |
|
|||||||||
|
ê |
51,12 |
62, 622 |
11,57 |
ú |
|
|
ê |
1,68 |
0,778 |
0,098 |
ú |
|
|
|
ë |
|
|
|
û |
|
|
ë |
|
|
|
û |
|
|
|
é -0,8 |
-0,9 |
-0,1ù |
|
|
é0, 429 |
0,5 |
0,071 |
ù |
|
|
|||
+ |
ê |
4,8 |
5, 4 |
0,6 |
ú |
-6t |
+ |
ê |
-3, 41 |
-3,9 |
-0,57 |
ú |
-8t |
. |
ê |
úe |
|
ê |
úe |
|
|||||||||
|
ê |
|
-32, 4 |
|
ú |
|
|
ê |
27,12 |
31, 6 |
4,502 |
ú |
|
|
|
ë-28,8 |
-3, 6û |
|
|
ë |
û |
|
|
||||||
|
|
é2ù |
|
é 2,742 ù |
é -1,6 |
ù |
é 0,858 ù |
||||||
eAt x |
= eAt × |
ê0 |
ú |
= |
ê-2,784úe-t + |
ê |
9,6 |
úe-6t + |
ê-6,816úe-8t . |
||||
0 |
|
ê |
ú |
|
ê |
|
ú |
ê |
|
ú |
ê |
|
ú |
|
|
ê |
ú |
|
ê |
3,36 |
ú |
ê |
|
ú |
ê |
54, 24 |
ú |
|
|
ë0 |
û |
|
ë |
û |
ë |
-57, 6û |
ë |
û |
|||
Так как y = x1, то свободная составляющая выходного сигнала будет рав-
на 2,742e-t -1,6e-6t + 0,858e-8t . Определим вынужденную составляющую при входном сигнале u(t) = 2*1(t). Сигнал на выходе при поступлении на вход1(t) уже вычислен – это переходная характеристика системы (4.1). Чтобы получить вынужденную составляющую сигнала в нашем случае, умножим переходную характеристику на 2.
Таким образом, сигнал на выходе системы будет следующим:
y (t )= 2, 742e-t -1,6e-6t + 0,858e-8t + 2(7,714e-8t - 9,6e-6t - 4,114e-t + 6) = (4.5) = -5, 478e-t - 20,8e-6t +16, 287e-8t +12.
Выполним проверку:
y(0) = -5, 478 - 20,8 + 16, 287 + 12 = 2 - верно; y(¥) = 12 - верно.
68
Найдем решение уравнений состояния, представленных в канонической
форме (4.4). |
Каждое |
из |
|
дифференциальных |
уравнений первого порядка |
||||||||
q&1 = xiqi + b1i |
зависит только от одной переменной, |
и его решение в общем виде |
|||||||||||
имеет вид |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(t) = q(0)elt + òB1u(t)el(t -t)dt. |
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Определим начальные условия q(0) |
для вектора q(t). |
|
|
|
|
||||||||
Так как |
q = M -1x(t) , то |
|
|
|
|
|
|
|
|
|
|||
éq1(0) |
ù |
é x1(0) ù |
é1,371 |
0, 4 |
0, 029ù é2 |
ù |
|
é2,742 |
ù |
||||
êq (0) |
ú = M -1 êx (0) |
ú |
= ê -0,8 |
-0,9 |
-0,1 ú ê0 |
ú |
= |
ê |
-1, 6 |
ú . |
|||
ê 2 |
|
ú |
ê 2 |
ú |
ê |
|
|
ú ê ú |
|
ê |
|
ú |
|
ê |
|
ú |
ê |
ú |
ê |
0,5 |
|
ú ê |
ú |
|
ê |
0,858 |
ú |
ëq3 (0) |
û |
ëx3 (0) |
û |
ë0, 429 |
0, 071û ë0 |
û |
|
ë |
û |
||||
Найдем выражения для q1(t), q2 (t) и q3(t).
t
q1 (t )= 2,742e-t + 2 × 4,11òe-(t -t)d t = 2, 742e-t + 8, 22(1 - e-t ) = -5, 478e-t + 8, 22;
0
t
q2 (t )= -1,6e-6t + 2 × 57, 6ò e-6(t -t)dt = -1,6e-6t +19, 2(1 - e-6t ) = -20,8e-6t +19, 2;
0
t
q3(t) = 0,858e-8t + 2(-61,71)ò e-8(t -t)dt = 0,858e-8t -15, 428(1 - e-8t ) =
0
= 16, 286e-8t -15,428.
В результате получим
y(t) = q1(t) + q2 (t) + q3 (t) = -5, 478e-t - 20,8e-6t + 16, 286e-8t + 12.
Выполним проверку:
y(0) = -5,478 - 20,8 +16, 287 +12 = 2 - верно; y(¥) = 12 - верно.
Решения нормальных и канонических уравнений состояния совпадают. Проверим, одинаково ли значение коэффициента усиления: по переда-
точной функции, переходной характеристике, моделям в пространстве состояний, аналитической записи импульсной переходной характеристики.
Проверим значение коэффициента усиления по передаточной функции:
W (S ® 0) = |
144S + 288 |
= |
288 |
= 6. |
S 3 + 15S 2 + 62S + 48 |
|
|||
|
48 |
|
||
69

По переходной характеристике:
h (t ® ¥) = 7,714e-8t - 9, 6e-6t - 4,114e-t + 6 = 6.
По моделям в пространстве состояний:
каноническая форма: 4,11 + 57,6 - 61,71 = 6; 6 8
нормальная форма (в установившемся режиме на входах интеграторов нули): -1872 + 144 ×15 - 48 × k = 0; k = 6;
по аналитической записи импульсной переходной характеристики:
W (t) = 4,114e-t + 57,6e-6t - 61,714e-8t ; проверяем: 4,11 + 57,6 - 61,71 = 6. 1 6 8
Мы видим, что значение коэффициента усиления одинаково.
Задание 2. Линейное программирование
Найти минимальное значение функции F (x) = 2x1 + 3x2 - x3 при следующих ограничениях:
ì2x1 + x2 - 3x3 ³ 6,
ï
íx1 - x2 + 2x3 = 4,
ï
îx1 + x2 + x3 £ 5,
x1 ³ 0, x2 ³ 0, x3 ³ 0 .
Домножим первое из ограничений на(-1) и введем в ограничения дополнительные переменные x4 , x5 и искусственную переменнуюR следующим образом:
ì- 2x1 - x2 + 3x3 + x4 = -6,
ï
íx1 - x2 + 2x3 + R = 4,
ï
îx1 + x2 + x3 + x5 = 5.
Пусть x4 , R и x5 – базисные переменные, а x1, x2 , x3 – небазисные. Функ-
ция цели F (x) = F (x) + M × å R =2x1 + 3x2 - x3 + M × (4 - x1 + x2 - 2x3 ).
В первой симплекс-таблице (табл. 4.1) коэффициенты при небазисных переменных в F-строке и M-строках знака не меняют, так как осуществляется минимизация функции. Свободный член в M-строке берется с противоположным знаком. Решение, соответствующее табл. 4.1, не является допустимым, так как есть отрицательный свободный член.
Выберем ведущий столбец и строку в соответствии с шагом2 алгоритма решения [18, подразд. 3.6]. После пересчета получим табл. 4.2. Оптимизация решения (шаг 5 алгоритма) осуществляется вначале по M-строке. В результате x3 введем в базис, а переменную R исключим из рассмотрения, сократив коли-
70

чество столбцов. После пересчета получим табл. 4.3, которая соответствует оптимальному решению задачи.
Таблица 4.1
БП |
Свободные |
|
Небазисные |
|
||
|
члены |
|
переменные |
|
||
|
|
х1 |
|
х2 |
|
х3 |
х4 |
-6 |
-2 |
|
-1 |
|
3 |
R |
4 |
1 |
|
-1 |
|
2 |
х5 |
5 |
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
F |
0 |
2 |
|
3 |
|
-1 |
|
|
|
|
|
|
|
M |
-4 |
-1 |
|
1 |
|
-2 |
Таблица 4.3
Таблица 4.2
БП |
Свободные |
|
Небазисные |
|
||
|
члены |
|
переменные |
|
||
|
|
х4 |
|
х2 |
|
х3 |
х1 |
3 |
-1/2 |
|
1/2 |
|
-3/2 |
R |
1 |
1/2 |
|
-3/2 |
|
7/2 |
х5 |
2 |
1/2 |
|
1/2 |
|
5/2 |
|
|
|
|
|
|
|
F |
-6 |
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
M |
-1 |
-1/2 |
|
3/2 |
|
-7/2 |
БП |
Свободные |
Небазисные |
Искомый минимум функции F(x) |
|||||||||||||||
|
члены |
переменные |
равен свободному |
членуF-строки |
||||||||||||||
|
|
х4 |
х2 |
|||||||||||||||
|
|
табл. 4.3, взятому |
с |
обратным зна- |
||||||||||||||
х1 |
24/7 |
-2/7 |
-1/7 |
|||||||||||||||
ком, |
так |
как minF(x) = -max(-F(x)); |
||||||||||||||||
х3 |
2/7 |
1/7 |
-3/7 |
|||||||||||||||
x4 = |
x2 = 0; |
x = |
24 |
; |
x |
= |
2 |
; |
x = |
9 |
; |
|||||||
х5 |
9/7 |
1/7 |
11/7 |
|||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
1 |
7 |
|
3 |
7 |
|
5 |
7 |
|
|||
F |
-46/7 |
5/7 |
20/7 |
F |
= 46 . |
|
|
|
|
|
|
|
|
|
|
|||
M |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||
min |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение задачи в Matlab
F=[2 3 -1];
A=[-2 -1 3;1 1 1;-1 0 0;0 -1 0;0 0 -1];
>>%коэффициенты левых частей неравенств, приведенных к знаку ≤,
>>%с учетом ограничений на знак
>>
B=[-6;5;0;0;0];
%правые части ограничений неравенств %для ограничения равенства
Aeq=[1 -1 2]; Beq=[4];
x=linprog(F,A,B,Aeq,Beq);
>>x
x = 3.4286 0.0000 0.2857
>>Q=F*x
Q=
6.5714
71

Найдем частично-целочисленное решение задачи, считая, что переменная x3 должна быть целой. Дополнительное ограничение составим по второй строке оптимальной симплекс-таблицы, которая соответствует базисной переменной x3. Ограничение записывается в соответствии с выражением
å aki wi |
+ |
|
{bk |
} |
åaki wi |
³ {bk } , |
{bk } |
|
|||||
iÎI + |
|
-1iÎI - |
|
|||
где aki – коэффициенты при небазисных переменных wi в рассматриваемой строке, {bk } – дробная часть свободного члена.
Тогда получим
2
|
1 |
x + |
|
|
7 |
|
(- |
3 |
)x |
2 |
³ |
2 |
|
или |
|
1 |
x + |
6 |
x ³ |
2 |
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
7 |
|||||||||||||||
7 4 |
|
|
- 1 |
7 |
|
7 |
|
4 |
35 2 |
7 |
|
||||||||||||
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вводим |
дополнительную |
переменнуюx6 |
и |
вносим |
ограничение в |
||||||||||||||||||
симплекс-таблицу (см. табл. 4.3 (М-строку исключаем) в результате получим табл. 4.4.
В качестве ведущего выбираем элемент в строкеx6, после перерасчета получим табл. 4.5.
Таблица 4.4
БП |
Свободные |
Небазисные |
|
|
члены |
переменные |
|
|
|
х4 |
х2 |
х1 |
24/7 |
-2/7 |
-1/7 |
х3 |
2/7 |
1/7 |
-3/7 |
х5 |
9/7 |
1/7 |
11/7 |
х6 |
-2/7 |
-1/7 |
-6/35 |
|
|
|
|
F |
-46/7 |
5/7 |
20/7 |
|
|
|
|
|
|
|
Таблица 4.5 |
|
БП |
Свободные |
Небазисные |
||
|
члены |
переменные |
||
|
|
х6 |
|
х2 |
х1 |
4 |
-2 |
|
1/5 |
х3 |
0 |
1 |
|
-3/5 |
х5 |
1 |
1 |
|
7/5 |
х4 |
2 |
-7 |
|
6/5 |
|
|
|
|
|
F |
-8 |
5 |
|
2 |
|
|
|
|
|
Оптимальное целочисленное решение x1 = 4, x5 = 1; x4 = 2, x1 =x3 = x6 = 0,
Fmax = 8.
Переход к двойственной задаче подробно рассмотрен в конспекте лекций и здесь не приведен.
|
Задание 3. Нелинейное программирование |
|
|
|||||
|
3.1. |
Найти |
экстремальное значение |
функцииF (x) = -2x2 |
+ 18x - |
|||
|
|
- x2 |
|
|
|
1 |
|
1 |
-2x x |
2 |
+ 12x |
2 |
методом наискорейшего |
спуска и методом |
Ньютона– |
||
1 |
2 |
|
|
|
|
|
||
Рафсона. Начальная точка x0 = [2; 1].
72
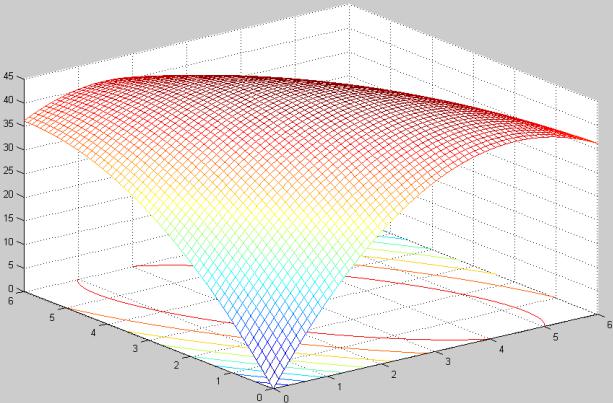
Вид функции цели можно посмотреть в пакете Matlab, используя подпрограмму:
[x1,x2]=meshgrid([0:0.1:6]); F=-2*x1.^2+18*x1-2*x1.*x2-x2.^2+12*x2; meshc(x1,x2,F);
На рис. 4.8 приведен вид функции F вместе с проекциями линии уровня: функция выпуклая вверх и имеет максимум.
Рис. 4.8
В методе наискорейшего спуска(подъёма) очередная точка при поиске
максимума функции вычисляется по формулеxk +1 = x k |
+ ak * ÑF (xk ) , где |
направление движения задается вектором градиента ÑF (x) |
функции F (x) , вы- |
численном в точке xk, а величина шага перемещения определяется числовым параметром α k.
ÑF (x) = |
é¶F ¶F |
ù |
= [-4x +18 - 2x ; -2x - 2x |
|
+12] |
; |
|||||
ê |
¶x |
|
¶x |
ú |
|
||||||
|
|
1 |
2 |
1 |
2 |
|
|
||||
|
ë |
1 |
2 |
û |
|
|
|
|
|
|
|
ÑF (x0 ) = [8; 6].
На первом шаге движение осуществляется из точкиx0 вдоль вектора ÑF (x0 ) в новую точку x1:
73

é |
1 |
ù é |
0 |
ù |
é8ù |
é |
+ 8a |
0 |
ù |
|
êx1 |
ú = êx1 |
ú + a0 |
ê ú |
= ê2 |
|
ú . |
||||
êx1 |
ú |
êx |
0 |
ú |
ë6û |
1 |
+ 6a0 |
û |
||
ë |
2 |
û |
ë |
2 |
û |
|
ë |
|
|
|
k
Величина шага α на любом шаге выбирается из условия обеспечения экстремума функции в рассматриваемом направлении. Подставляя координаты точки x1 в функцию F (x) , получим
F (a0 ) = -2(2 + 8a0 )2 +18(2 + 8a0 ) - 2(2 + 8a0 )(1 + 6a0 ) - -(1 + 6a0 )2 +12(1 + 6a0 ) = -260(a0 )2 + 100a0 + 35;
¶F = -520a0 +100 = 0 ; a0 = 0,192 .
¶a0
В результате после первого шага координаты очередной точки получаются равными:
|
|
x1 = 2 + 8a 0 |
= 2 + 8 × 0,192 = 3,54; |
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x12 |
= 1 + 6a 0 |
= 1 + 6 × 0,192 = 2,15. |
|||||||||
Вычисляется ÑF (x1) . Если |
|
ÑF (x1) |
|
|
|
£ ε (ε – точность решения задачи), |
|||||||
|
|
|
|||||||||||
поиск прекращается и считается, |
что x*= x1. Если нет, переходят к шагу2. |
||||||||||||
ÑF (x1 ) =[-0,46; 0,62]. Пусть ε £ 0,1, тогда |
|||||||||||||
ÑF (x1 ) = |
æ |
¶F |
ö |
2 |
æ |
¶F |
ö2 |
|
|
|
|
||
ç |
¶x |
÷ |
+ |
ç |
¶x |
|
÷ |
= (0,46)2 + (0,62)2 = 0,59 = 0,768 . |
|||||
|
ç |
÷ |
|
ç |
2 |
÷ |
|
|
|
|
|
||
|
è |
1 |
ø |
|
è |
|
ø |
|
|
|
|
|
|
На втором |
шаге |
движение |
осуществляется |
в направлении вектора |
|||||||
ÑF (x1) с величиной шага a1: |
|
|
|
|
|
|
|
||||
éx2 |
ù |
é3,54ù |
+ a1 |
é- 0,46ù |
é3,54 |
- 0,46a1 |
ù |
||||
ê |
1 |
ú = ê |
ú |
ê |
ú |
= ê |
2,15 |
+ 0,62a1 |
ú ; |
||
êx2 |
ú |
ë2,15û |
|
ë 0,62 û |
ë |
û |
|||||
ë |
2 |
û |
|
|
|
|
|
|
|
||
F (a1 ) = -0,24(a1 )2 + 0,6a1 + 44,8 ;
dF = -0,48a1 + 0,6 = 0 ; a1 =1,25; da1
x12 = 3,54 - 0,46 ×1,25 = 2,965;
x22 = 2,15 + 0,62 ×1,25 = 2,92 ;
ÑF (x 2 ) = [0,32; 0,24];
ÑF (x2 ) =  0,322 + 0,242 = 0,16 = 0,4 .
0,322 + 0,242 = 0,16 = 0,4 .
74
Заданная точность не обеспечена, следует сделать еще один шаг, в результате которого точка экстремума определится координатамиx* = x3 = [3; 3],
Fmax = 45.
Рассмотрим графическую интерпретацию решения задачи.
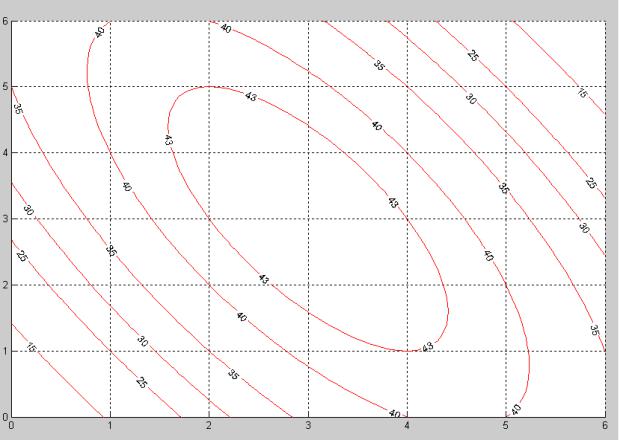
На плоскости x1, x2 (рис. 4.9) приведены линии уровня функции цели F, построенные в Matlab, в соответствии с подпрограммой:
>>[x1,x2]=meshgrid([0:0.1:6]);
>>F=-2*x1.^2+18*x1-2*x1.*x2-x2.^2+12*x2;
>>figure;
>>cl=[15 25 30 35 40 43 45];
>>[c,h]=contour3(x1,x2,F,cl,'r');
>>clabel(c,h);
>>view(0,90);
>>
Рис. 4.9
Центр концентрических линий является точкой экстремума x*.
В процессе поиска траектория движения должна из начальной точкиx0 привести в конечную точку x* (рис. 4.10).
75

Рис. 4.10
Следует обратить внимание на то, что каждая очередная точка лежит на направлении вектора градиента, вычисленного в этой точке, и каждое последующее направление перпендикулярно предыдущему.
Решим эту же задачу методом Ньютона– Рафсона. Очередная точка поиска вычисляется в соответствии с выражением
xk +1 = xk - H -1 (xk )ÑF (xk ) ,
где H (x) – матрица Гессе функции F (x); H -1(x) |
– обратная по отношению |
||||||||||||||||||
к H (x) матрица. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é¶F ¶F ù |
= [–4x1 –2x2 + 18; |
–2x1 – 2x2 +12 ]; |
|||||||||||||
ÑF (x) = ê |
|
|
|
|
|
|
|
ú |
|||||||||||
¶x |
|
¶x |
2 |
||||||||||||||||
|
|
|
ë |
1 |
|
|
û |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ÑF (x0 ) =[8; 6]; |
|
|
|
|
|
é |
¶2 F |
|
|
¶2 F |
ù |
|
|
|
|
|
|
||||||||
ê |
|
|
2 |
|
|
|
|
|
|
|
ú |
é- 4 - 2ù |
|
1 |
|
||||
|
|
¶ ¶ |
|
|
|
|
|
||||||||||||
H (x) = ê |
¶x1 |
|
|
x1 x2 |
ú |
; H (x) = ê |
|
ú ; |
H -1 = |
|
× AdjH , |
||||||||
|
|
- |
det H |
||||||||||||||||
ê |
¶2 F |
|
|
¶2 F |
ú |
ë- 2 |
2û |
|
|
||||||||||
ê |
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
||||
¶x |
2 |
¶x |
|
|
¶x2 |
|
|
|
|
|
|
|
|
||||||
ë |
|
1 |
|
|
|
|
2 |
|
|
û |
|
|
|
|
|
|
|||
где det H – определитель |
матрицы H ; AdjH – присоединенная к H матрица |
|||||||
(транспонированная матрица алгебраических дополнений). |
матрицыH : |
|||||||
Найдем |
алгебраические |
дополнения |
|
элементов |
||||
Ñij = (-1)i + j m |
, тогда D |
= -2 ; Ñ |
= +2 ; Ñ |
21 |
= +2 ; D |
22 |
= -4 . |
|
ij |
11 |
12 |
|
|
|
|
||
76 |
|
|
|
|
|
|
|
|
Соответственно
|
|
|
AdjH = |
é- 2 |
2 ù |
det H = 4 ; |
H -1 |
é- 0,5 |
0,5ù |
, |
|
|
|
|
|
|||||||
|
|
|
ê |
2 |
|
ú ; |
= ê |
|
|
ú |
|
|
|
|
|
|||||||
|
|
|
|
ë |
|
- 4û |
|
|
|
|
|
ë 0,5 |
-1û |
|
|
|
|
|
|
|||
é x1 |
ù |
é2 ù |
é-0, 5 |
|
0, 5 ù é8 ù |
= |
é2 ù |
- |
é-4 |
+3ù |
= |
é2 ù |
- |
é -1ù |
= |
é3ù |
; |
|||||
ê 1 |
ú = |
ê ú |
- ê |
|
|
-1 |
ú ê ú |
ê ú |
ê |
4 |
ú |
ê ú |
ê |
-2 |
ú |
ê ú |
||||||
ê x1 |
ú |
ë1 û |
ë 0, 5 |
|
|
û ë6 û |
|
ë1 û |
|
ë |
-6 û |
|
ë1 û |
|
ë |
û |
|
ë3 û |
|
|||
ë 2 |
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ÑF (x1 ) = [-12 + 18 - 6; -6 - 6 + 12] = [0; 0].
Следовательно, в точке x1 =[3; 3] функция F(x) достигает максимального значения Fmax = 45.
|
3.2. |
|
|
Найти |
|
максимальное |
значение |
|
функцииF (x) = -2x2 |
+ 18x - |
||||||||||||||||||||||
|
|
|
- x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
||
- 2x x |
2 |
+12x |
2 |
при ограничениях |
2x + x |
2 |
|
³ 2 |
, x |
+ x |
2 |
£ 4 |
, |
x |
³ 0 |
, x |
2 |
³ 0 |
||||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|||||
методом допустимых направлений Зойтендейка. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Начальная точка x 0 =[2; 1]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
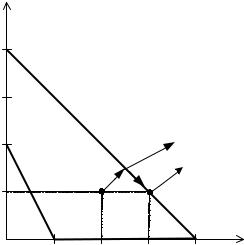
|
Область |
допустимых |
значений |
-пе x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ременных (ОДЗП) приведена на рис. 4.11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Последовательность решения задачи: |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1. |
Находится |
направление |
вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
градиента в точке x0 , ÑF (x0 ) =[8; |
6], то- |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
гда |
|
|
координаты |
|
|
очередной |
|
точ |
|
|
|
|
|
|
|
|
|
|
ÑF (x1) |
|
|
|
||||||||||
1 |
|
|
|
0 |
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x1 = 2 |
+ |
8a |
|
; |
x2 |
=1 + 6a |
|
(см. предыдущий |
2 |
|
|
|
|
|
|
|
x1 |
|
|
ÑF (x2 ) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пример). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ÑF (x0 ) |
|
|
S1 |
2 |
|
|
|
|||||
|
2. Определяем интервал допустимых |
1 |
|
|
|
|
|
x0 |
|
|
|
x |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
значений для параметра a0 , при котором |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
точка х1 будет |
принадлежать |
ОДЗП. Для |
0 |
|
|
|
1 |
2 |
|
|
3 |
4 |
|
x1 |
||||||||||||||||||
этого координаты точки х1 подставляются |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
в ограничения задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.11 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
ì2(2 + 8a0 ) + (1 + 6a0 ) ³ 2 |
|
|
|
a0 ³ -0,136; |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
ï |
+ 8a0 +1 + 6a0 £ 4 |
|
|
|
a0 |
£ 0,071; |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
ï2 |
Þ |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
í |
+ 8a0 ³ 0 |
|
|
|
a0 £ -0,25; |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
ï2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
ï |
+ 6a |
0 |
³ 0 |
|
|
|
|
|
a |
0 |
³ -0,167. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
î1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Выбираем наиболее сильные из полученных условий, тогда
-0,135 £ a0 £ 0,071.
3.Находим величину α0, которая обеспечит максимум функции F(x). Процедура полностью совпадает с первым шагом решения задачи методом наиско-
77

рейшего спуска, поэтому α0 = 0,192. Это значение α0 не принадлежит найденному интервалу (п. 2), поэтому принимается, что α0 = 0,071. При этом очередная точка х1 поисковой траектории оказывается на границе области и находится на прямой, соответствующей уравнению x1 + x2 = 4 . Координаты точки х1 и значе-
ние градиента функции в этой точке ÑF (x1 ) определяются выражениями:
x11 = 2 + 8a0 = 2 + 0,568 = 2,568;
x12 =1 + 6a0 =1 + 0,425 =1,425;
ÑF (x1 ) = [5,12; 4,01].
4. Движение в направлении ÑF (x1 ) |
выводит за пределы ОДЗП, поэтому |
|||||||||
очередная |
точка поиска вычисляем |
по |
k +1 |
= x |
k |
+ a |
k |
S |
k |
, где |
выражениюa |
|
|
|
|||||||
S k – новое |
направление движения, которое |
составляет минимальный |
острый |
|||||||
угол с вектором градиента и направлено либо внутрь, либо по границе ОДЗП. При этом очередная точка должна принадлежать ОДЗП, а функция цели при переходе к очередной точке должна увеличиваться максимальным образом.
Направление S k |
находим, как решение задачи: |
|
|
|
|
|
||||||||
|
|
max{ÑF T (xk ) × S k ¶ | aTj S k |
£ 0, || S k ||£1}. |
|
|
|
|
|||||||
Направление S1 очередного шага определяем из условия |
|
|
|
|
||||||||||
|
|
|
|
|
éS1 |
ù |
S1 |
+ S1 = 0 |
, |
|
|
|
|
|
|
|
|
aT S1 = [1 1] ê |
1 |
ú = |
|
|
|
|
|||||
|
|
|
j |
|
êS1 |
ú |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
ë |
1 |
û |
|
|
|
|
|
|
|
где aTj – вектор коэффициентов при переменных во втором ограничении, на ко- |
|
|||||||||||||
тором находится точка х1. |
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда |
|
следует, |
что |
S1 |
= -S1 |
, |
тогда |
S1 = |
(S1)2 |
+ (S1 )2 |
=1; |
|||
|
|
|
|
|
2 |
|
1 |
|
|
|
1 |
2 |
|
|
2(S1)2 =1; |
S1 |
= 1 = |
1 |
= 0,71; |
S1 |
= -0,71. Таким образом, |
max ÑF T (x ) × S |
1 |
||||||
1 |
1 |
2 |
1,41 |
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
достигается при S11 = 0,71; S21 = -0,71. |
|
|
|
|
|
|
|
|
||||||
При движении из точки x1 |
в точку |
x 2 |
следует двигаться по граничной |
|||||||||||
прямой в направлении S1, как показано на рис. 4.11. |
|
|
|
|
|
|||||||||
5.Координаты точки х2 определяются выражением
x2 = x1 + a1S1
или
é x2 |
ù |
é2, 568ù |
|
é 0, 71 |
ù |
é2, 568 |
+ 0, 71a1 |
ù |
||||
ê |
1 |
ú = ê |
|
ú |
1 |
|
ú |
= ê |
|
ú . |
||
|
1, 426 |
+ a |
ê |
|
- 0, 71a1 |
|||||||
ê x2 |
ú |
ë |
û |
|
ë |
-0, 71û |
ê1, 426 |
ú |
||||
ë |
2 |
û |
|
|
|
|
|
|
|
ë |
|
û |
78

Находим интервал изменения a1, при котором х2 |
принадлежит ОДЗП: |
||
ì2(2,568 + 0, 71a1) +1, 426 - 0,071a1 ³ 2, |
ìa1 ³ -6, 42, |
||
ï |
1 |
ï |
1 |
ï |
ï |
||
í |
2,568 + a ³ 0, |
Þía ³ -3,62, |
|
ï |
1 |
ï |
1 |
ï |
1, 426 - 0,71a ³ 0 |
ï a ³ 2,01. |
|
î |
|
î |
|
Второе ограничение опущено, так как точка х2 принадлежит соответствующей ему прямой, тогда - 3,62 £ a0 £ 2,01.
6. Находим a1, которое обеспечит максимум функции F(x) в направлении S1.
Для этого координаты точки х2 подставляются в функцию F(x), тогда
F (a1) = 29,58 -1,01(a1)2 +1,22a1 ;
dF = -2,02a1 +1,22 = 0 , a1 = 0,6 , da1
Значение a1 принадлежит интервалу, найденному в п. 5, поэтому для расчета координат точки х2 принимается a1 = 0,6 :
x12 = 2,568 + 0,71× 0,6 = 2,994 » 3;
x22 =1,425 - 0,71× 0,6 = 0,999 »1.
Вычисляются составляющие вектора градиента в точке х2:
|
|
|
ÑF (x 2 ) = [- 4 × 3 +18 - 2 ×1;-2 × 3 - 2 ×1 +12]=[4; 4]. |
|
|
||||||||||
Направление вектора ÑF (x 2 ) |
перпендикулярно направлению S1, следо- |
||||||||||||||
вательно, найденная точка х2 = [3; |
1] обеспечивает максимум |
функции F(x) |
|||||||||||||
с учетом ограничений на переменные: Fmax = 41. |
|
функцииF (x) = -2x2 |
|
||||||||||||
3.3. |
Найти |
максимальное |
значение |
|
+ 18x - |
||||||||||
|
|
- x2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
- 2x x |
2 |
+12x |
2 |
при ограничениях 2x + x |
2 |
³ 2 ; |
x |
+ x |
2 |
£ 4 ; |
x |
³ 0 , исполь- |
|||
1 |
2 |
|
|
1 |
|
1 |
|
|
1,2 |
|
|
||||
зуя условия теоремы Куна – Таккера. |
|
|
|
|
|
|
|
|
|
|
|||||
Последовательность решения задачи: |
|
|
|
|
|
|
|
|
|
||||||
1. |
Составляем функцию Лагранжа: |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
L(x,l) = F (x) + lT g(x) = F (x) + ål j × g j (x) . |
|
|
|
||||||||
Здесь g j (x) |
|
|
|
|
|
j |
|
|
|
|
|
|
|
||
– левые части ограничений, приведенных к нулевой правой части; |
|||||||||||||||
l j – неопределенные множители Лагранжа: |
|
|
|
|
|
|
|
|
|
||||||
g1(x) = -2 + 2x1 + x2 ³ 0; g2 (x) = 4 - x1 - x2 ³ 0 .
79
Точка экстремума является седловой точкой с максимумом поx и минимумом по l, поэтому ограничения приведены к виду g j (x) ³ 0 :
L(x,l) = -2x12 + 18x1 - 2x1x2 - x22 + 12x2 + l1(-2 + 2x1 + x2 ) + l2 (4 - x1 - x2 ) .
2. Условия теоремы Куна – Таккера записываем следующим образом:
ì |
|
|
¶ L |
|
|
|
|
|
|
|
|
£ |
0 , |
||
|
|
|
|
|
|
|
|
|
|
||||||
ï |
|
|
|
|
|
|
|
|
x * |
, l * |
|||||
|
|
¶ x i |
|
|
|
||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
ï |
x |
* |
|
¶ L |
|
|
|
|
|
|
= 0 , |
||||
|
|
|
|
|
|
|
|||||||||
í |
|
|
|
|
|
|
|
|
|
x |
* |
, l |
* |
||
i |
¶ x i |
|
|
||||||||||||
ï |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
ï |
|
* |
³ 0 , i = 1 , n . |
||||||||||||
ï |
|
x i |
|
||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
|
¶ L |
|
|
|
|
|
|
|
³ 0 , |
||
|
|
|
|
|
|
|
|
||||||
ï |
|
|
|
|
|
|
|
x * , l * |
|||||
|
¶ l j |
|
|
||||||||||
ï |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
ï |
* |
|
¶ L |
|
|
|
|
|
* = 0 , |
||||
|
|
|
|
|
|
||||||||
í l |
|
j |
|
|
|
|
|
|
|
x |
* |
, l |
|
|
|
¶ l j |
|
|
|||||||||
ï |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
ï |
|
x *j ³ 0 , j = 1, n . |
|||||||||||
ï |
|
||||||||||||
î
Частные производные функции Лагранжа определяются выражениями:
|
|
¶L |
|
= -4x +18 - 2x + 2l - l |
2 |
£ 0 ; |
|||||||
|
|
|
|
||||||||||
1 |
|
2 |
1 |
|
|
|
|||||||
|
|
¶x1 |
|
|
|
|
|
|
|
|
|||
|
|
|
¶L |
= -2x |
- 2x +12 + l - l |
2 |
£ 0 ; |
|
|||||
|
|
|
|
|
|||||||||
1 |
2 |
|
1 |
|
|
||||||||
|
|
|
¶x2 |
|
|
|
|
|
|
|
|
||
¶L |
= -2 + 2x + x ³ 0 ; |
|
¶L |
= 4 - x - x ³ 0 . |
|||||||||
|
|
|
|||||||||||
1 |
2 |
|
¶l2 |
|
|
1 |
2 |
||||||
¶l1 |
|
|
|
|
|
|
|||||||
Для приведения неравенств к виду равенств вводятся дополнительные неотрицательные переменные V и W. Одновременно свободные члены переносятся в правую часть, тогда
-4x1 + 18 - 2x2 + 2l1 - l2 + V1 = -18 , |
-2x1 - 2x2 + 12 + l1 - l2 + V2 = -12 , |
2x1 + x2 -W1 = 2 , |
- x1 - x2 -W2 = -4 . |
Решение этой системы из четырех алгебраических уравнений, содержащих восемь неизвестных, можно найти с помощью симплекс– процедуры. На первом шаге в базис включаются все введенные дополнительные переменные, тогда первая симплекс-таблица соответствует табл. 4.6. Строка для функции
цели |
|
отсутствует. Процедура |
решения иллюстрируется симплекс– табли- |
|||||||
цами (табл. 4.6 – 4.9). |
|
|
|
|
||||||
|
В каждой из таблиц выделен ведущий элемент. Решение, определяемое |
|||||||||
табл. 4.9, соответствует допустимому |
базисному решениюx1=3; |
x2=1; W1=5; |
||||||||
l2 = 4 ; V1 = V2 = λ1 = W2 = 0. Кроме |
того, выполняется условие |
x1v1 = x2v2 = |
||||||||
= l w |
= l |
2 |
w |
2 |
= 0, поэтому |
x* = 3 , x* |
= 1 является оптимальным решением за- |
|||
1 |
1 |
|
|
|
1 |
2 |
|
|
||
дачи Fmax = 41.
80

Таблица 4.6
БП. |
Св. чл. |
Небазисные переменные |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x1 |
|
x2 |
|
l1 |
l2 |
|
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
v1 |
-18 |
-4 |
|
-2 |
|
|
|
2 |
|
|
-1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
v2 |
-12 |
-2 |
|
-2 |
|
|
|
1 |
|
|
-1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
w1 |
-2 |
-2 |
|
-1 |
|
|
|
0 |
|
|
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
w2 |
4 |
1 |
|
1 |
|
|
|
0 |
|
|
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.8 |
|||||||||||
|
|
Небазисные переменные |
|||||||||||||||||||||
БП. |
Св. чл. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v1 |
|
v2 |
l1 |
|
l2 |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x1 |
3 |
- |
|
1 |
|
|
|
1 |
|
|
- |
|
1 |
|
|
0 |
|
|
|
||||
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x2 |
3 |
- |
|
1 |
|
|
- |
|
1 |
|
|
0 |
|
|
|
|
1 |
|
|
|
|||
|
|
2 |
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
w1 |
7 |
- |
1 |
|
|
|
0 |
|
|
-1 |
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
w2 |
-2 |
|
0 |
|
|
|
1 |
|
|
|
1 |
|
|
|
- |
1 |
|
|
|||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
Таблица 4.7
БП. |
Св. чл. |
Небазисные переменные |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x1 |
v2 |
|
l1 |
l2 |
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v1 |
-6 |
-2 |
|
-1 |
|
|
1 |
|
|
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
6 |
|
1 |
|
|
- |
1 |
|
- |
1 |
|
|
1 |
|
|
||||||
|
|
|
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
||||||||
w1 |
4 |
-1 |
|
- |
1 |
|
- |
1 |
|
|
1 |
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
||||||||
w2 |
-2 |
|
0 |
|
|
|
1 |
|
|
|
1 |
|
|
- |
1 |
|
|||||
|
2 |
|
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.9 |
|||||||||
|
|
Небазисные переменные |
|||||||||||||||||||
БП. |
Св. чл. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v1 |
v2 |
|
l1 |
w2 |
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x1 |
3 |
- |
|
1 |
|
|
1 |
|
|
- |
|
1 |
|
0 |
|
|
|||||
|
|
2 |
|
2 |
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x2 |
1 |
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|||||
|
|
|
2 |
|
|
4 |
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
w1 |
5 |
- |
1 |
|
|
1 |
|
|
- |
1 |
|
1 |
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
l2 |
4 |
|
0 |
|
|
-1 |
|
-1 |
|
-1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.4. Найти максимальное значение функции F (x) = -2x |
2 |
|
+ 18x |
- 2x x |
2 |
- |
||||||||||||||||||||||||
-x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
1 |
|
||||||
+ 12x |
2 |
при ограничениях |
2x + x ³2, |
x |
+ x |
2 |
£ 4 , |
x ³ 0 |
, |
|
x |
2 |
³ 0 |
методом |
|||||||||||||||||
2 |
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
линейных комбинаций. Начальная точка x 0 = [2; 1]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Область допустимых значений пере- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
менных (ОДЗП) приведена на рис. 4.12. |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Суть |
метода |
линейных |
комбинаций |
|
|
|
1* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
заключается в линеаризации функцииF(x) |
|
4 |
|
|
|
x% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
и замене ее линейной функциейw(x) в со- |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ответствии с выражением |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
w(x) = ÑF (x)т × x. |
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
x2 |
= x* |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Последовательность решения задачи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x%0* |
|
|
|
|
||||||||||
|
1. Находим направление |
вектора гра- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|||||||
диента в точке x0; |
ÑF (x0 ) = [8, 6], |
в соот- |
|
|
|
|
1 |
2 |
3 |
|
4 |
|
|
|
|
||||||||||||||||
ветствии с этим |
é] x1 ù |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.12 |
|
|
|
|
|
|
|
||||||||||
|
w(x0 ) = [8, 6 |
= 8x + 6x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
ê |
ú |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë x2 |
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81 |
2. Решаем задачу линейного программированияw(x0 ) = 8x1 + 6x2 (max) при ограничениях 2x1 + x2 ³ 2, x1 + x2 £ 4, x12 ³ 0.
В результате получаем одну из вершин ОДЗП x%0* =[4, 0]. Это оптималь-
ное решение линеаризованной задачи (см. рис. 4.12).
3. Произведем корректировку найденного решения в соответствии с выражением
|
|
|
|
|
|
|
x1 = x0 + a0 (x%0* - x0 ) |
|
|
|
||
|
é x1 |
ù |
é2ù |
é4 - 2 ù |
é2 + 2a0 ù |
|
|
|
||||
или ê 1 |
ú = ê |
ú |
+ a0 ê |
ú |
= ê |
ú . |
|
|
|
|||
|
ê x1 |
ú ë1 |
û |
ë 0 - 1 |
û ê 1 - a0 |
ú |
|
|
|
|||
|
ë 2 |
û |
|
|
|
|
|
ë |
û |
|
|
|
|
4. Находим значение a0 , которое максимизирует F (x1). Подставляя x1 |
и |
||||||||||
x12 в F (x) , получим |
|
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|||||||
|
F (a0 ) = -2(2 + 2a0 )2 + 18(2 + 2a0 ) - 2(2 + 2a0 )(1 - a0 ) - (1 - a0 )2 + |
|
|
|||||||||
|
|
|
|
|
|
+12(1 - a0 ) = -5(a0 )2 + 10a0 + 35. |
|
|
|
|||
|
Тогда |
|
¶F |
= - 10a0 + 10 = 0, отсюда a0 = 1. |
|
|
|
|||||
|
|
¶a0 |
|
|
|
|||||||
|
|
|
|
|
определяются следующим образом: x1 |
= 2 + 2a0 |
|
|
||||
|
Координаты точки x1 |
= 4; |
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x1 |
= 1 - a0 = 0. В рассматриваемом случае точкаx1 совпала с точкой x%0*, но в об- |
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
щем случае она должна принадлежать прямой, соединяющей точки x0 и x%0*.
5.Осуществляем линеаризацию F (x) относительно найденной точки x1 .
ÑF (x1) = [2, 4], тогда w(x1) = 2x1 + 4x2.
6.Решаем задачу линейного программированияw(x1) = 2x1 + 4x2 (max) при ограничениях 2x1 + x2 ³ 2, x1 + x2 £ 4, x12 ³ 0.
Оптимальное решение достигается в вершине ОДЗП x%1* = [0, 4].
7.Точка x2 , соответствующая скорректированному решению, должна
принадлежать прямой, соединяющей x1 и x%1* (в нашем случае это правая граница ОДЗП) x2 = x1 + a1(x%1* - x1) или
é x2 |
ù |
é4 ù |
+ a1 |
é0 - 4ù |
é4 - 4a1 ù |
|
||
ê 1 |
ú = ê ú |
ê |
ú |
= ê |
ú . |
|
||
ê x2 |
ú ë0 û |
|
ë4 |
- 0û |
ê0 + 4a1 |
ú |
|
|
ë 2 |
û |
|
|
|
|
ë |
û |
|
8. Находим значение a1, которое максимизируетF (x2 ). Подставляя x2 |
и |
|||||||
|
|
|
|
|
|
|
1 |
|
x22 в F (x) , получим
82

F (a1) = -2(4 - 4a1)2 + 18(4 - 4a1) - 2(4 - 4a1)(0 + 4a1) - (0 + 4a1)2 + +12(0 + 4a1) = -16(a1)2 + 8a1 + 40.
Тогда ¶F = - 32a1 + 8 = 0 и a1 = 0, 25.
¶a0
Координаты точки x2 будут равны x12 = 4 - 4a1 = 3; x22 = 4a1 = 1. Это и есть точка экстремума, полученные данные совпадают с результатом, полученным предыдущими методами.
83
|
СОДЕРЖАНИЕ |
|
1. |
Рабочая программа по дисциплине «математические основы теории систем»..................... |
3 |
|
1.1. Цель и задачи преподавания дисциплины ........................................................................ |
3 |
|
1.2. Методические указания ..................................................................................................... |
4 |
|
1.3. Содержание дисциплины .................................................................................................. |
4 |
|
1.4. Курсовая работа, ее характеристика ............................................................................... |
11 |
|
1.5. Контрольные работы, их характеристика ....................................................................... |
12 |
|
Литература.............................................................................................................................. |
13 |
2. |
Задания по выполнению контрольной работы ...................................................................... |
16 |
3. |
Варианты заданий по курсовой работе ................................................................................. |
44 |
4. |
Методические указания и примеры выполнения заданий по курсовой работе ................... |
54 |
84

Св. план 2011, поз. 32
Учебное издание
Павлова Анна Валентиновна
МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ СИСТЕМ
Методическое пособие для студентов специальности 1-53 01 07 «Информационные технологии
и управление в технических системах» заочной формы обучения
Редактор Н. В. Гриневич
Подписано в печать |
Формат 60´84 1/16. |
Бумага офсетная. |
Гарнитура «Таймс». |
Печать ризографическая. |
Усл. печ. л. |
Уч.-изд. л. 5,0. |
Тираж 100 экз. |
Заказ 814. |
|
|
|
Издатель и полиграфическое исполнение: Учреждение образования «Белорусский государственный университет информатики и радиоэлектроники» ЛИ №02330/000494371 от 16.03.2009. ЛП №02330/0494175 от 03.04.2009. 220013, Минск, П.Бровки, 6.
85
