
- •Содержание
- •Лекция №1 регулирование угловой скорости двигателя постоянного тока с независимым возбуждении при якорном управлении.
- •Лекция №2 полюсное управление угловой скоростью
- •Лекция №3 динамические характеристики микродвигателей постоянного тока
- •Лекция №4 универсальные коллекторные микродвигатели
- •Лекция №5 двухфазные асинхронные микродвигатели
- •Лекция №6 методы расчета параметров двухфазных асинхронных двигателей
- •Лекция №7 способы управления исполнительными асинхронными микродвигателями
- •Лекция №8 динамические характеристики исполнительных асинхронных микродвигателей
- •Лекция №9 микродвигатели с расщепленными экранированными полюсами.
- •Лекция №10 асинхронные микродвигатели с пусковыми элементами
- •Лекция №11 синхронные микродвигатели с постоянными магнитами на роторе
- •Лекция №12 реактивные микродвигатели
- •Лекция №13 гистерезисные микродвигатели
- •Лекция №14 применение синхронных микродвигателей; шаговые микродвигатели
- •Лекция №15 режимы работы шаговых двигателей; характеристики шаговых двигателей; области применения шаговых двигателей
- •Лекция № 16 измерительные приборы, используемые при отладке информационного канала автоматизированногоэлектропривода; измерители амплитудно_частотных характеристик
- •Отклонение зависимости fгкч(Up) от линейной приводит к искажению ачх, наблюдаемой на экране прибора. Существует несколько способов линеаризации зависимостиfгкч(Up).
- •Лекция №17 методы измерения фазового сдвига
- •Лекция №18 электронные цифровые частотомеры; цифровые вольтметры
- •Использованная литература
Лекция №6 методы расчета параметров двухфазных асинхронных двигателей
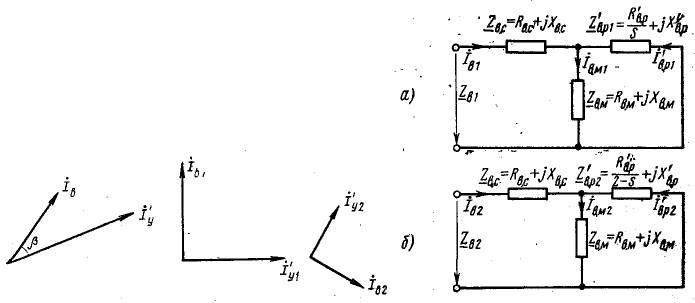
Рис. 2.7 Рис. 2.8
Составим уравнение электромагнитного вращающего момента исполнительного асинхронного микродвигателя. Форма магнитного поля в двигателе в общем случае эллиптическая, причем эллиптичность вызвана асимметрией м.д.с. обмоток В и У, т. е. нарушением хотя бы одного из условий кругового поля. Поскольку в большинстве двигателей пространственный угол между обмотками γ = 90°, можно перейти от асимметрии м.д.с. к асимметрии приведенных токов в обмотках В и У статора двигателя. Это значит, что угол сдвига β векторов Iу и Iв во времени отличен от 90°, а значения модулей, приведенных к числу витков обмотки возбуждения ωв, не равны:
![]() ,
,
где kтр = ωв.эф/ωу.эф – коэффициент трансформации обмоток В и У.
Чтобы при определении токов и вращающего момента в исполнительном асинхронном микродвигателе можно было использовать методику расчета асинхронных микродвигателей с симметричным питанием, разработанную в общем, курсе электрических машин, воспользуемся методом симметричных составляющих в применении к двухфазным системам.
Согласно этому методу, несимметричная двухфазная система неодинаковых векторов токов Iв и I'у (рис. 2.7), сдвинутых между собой на произвольный угол, может быть разложена на две симметричные системы, состоящие каждая из двух векторов; одинаковых по длине и сдвинутых между собой на угол 90°. Система векторов прямой последовательности (Iв1, I'у1) имеет то же чередование фаз, что и исходная система. Система векторов обратной последовательности (Iв2, I'у2) имеет противоположное чередование фаз. При этом
![]() ;
; ![]() . (2.1)
. (2.1)
Эквивалентность исходной и полученной систем имеет место, если
![]() ;
; ![]() . (2.2)
. (2.2)
Составим схемы замещения двигателя, необходимые для определения токов в обмотках статора и ротора. При одинаковой конструктивной схеме обмоток параметры схем замещения обмоток В и У в приведенной форме примерно равны и схему замещения достаточно составить только для обмотки В.
Схемы замещения составляют раздельно для прямой (рис. 2.8, а) и обратной (рис. 2.8, б) последовательностей, поскольку поля прямой и обратной последовательностей вращаются относительно ротора с разной угловой скоростью и, следовательно, выражения для скольжений и полных сопротивлений в схемах замещений получаются разными. Скольжение ротора относительно поля обратной последовательности
![]() , (2.3)
, (2.3)
где ω2 – угловая скорость ротора; ω1 – синхронная угловая скорость; s – скольжение ротора относительно поля прямой последовательности.
На роторных участках схем замещения ставят соответственно s или 2 - s.
На рис. 2.8 обозначено: Rв.с и Хв.с - активное и индуктивное сопротивления статорной обмотки В; R'в.р и X'в.р – активное и индуктивное сопротивления ротора, приведенные к числу фаз статора и числу витков обмотки В; Rв.м и Хв.м – активное и индуктивное сопротивления обмотки В, соответствующие магнитному потоку взаимоиндукции статора и ротора; Zв1 и Zв2 – полные сопротивления схем замещения для прямой и обратной последовательностей.
Значения этих сопротивлений определяют расчетным или экспериментальным путем.
Если в цепь обмотки возбуждения двигателя включают последовательно фазосдвигающий элемент, то его сопротивление Ζф должно быть введено в статорный участок схемы замещения обмотки В, т. е. последовательно с Zb.с. При этом методика расчета токов и вращающего момента не изменяется, однако расчетные уравнения несколько усложняются.
Напряжение U1 на зажимах обмотки возбуждения и напряжение на зажимах обмотки управления Uу' = kтpUy уравновешиваются падениями напряжения от токов обеих последовательностей на сопротивлениях соответствующих схем замещения, т. е.
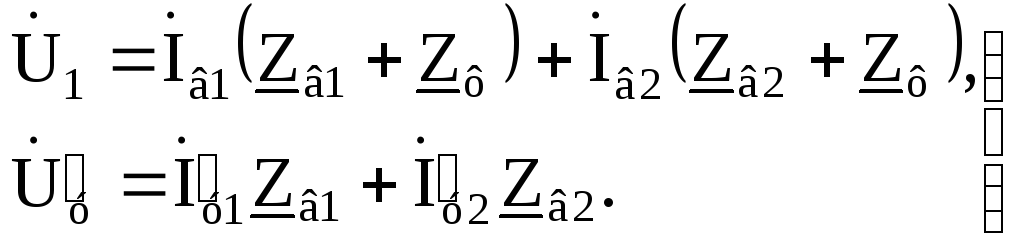 (2.4)
(2.4)
Решаем систему (2.4) с учетом (2.1) и получаем выражения симметричных составляющих токов обмоток фаз:
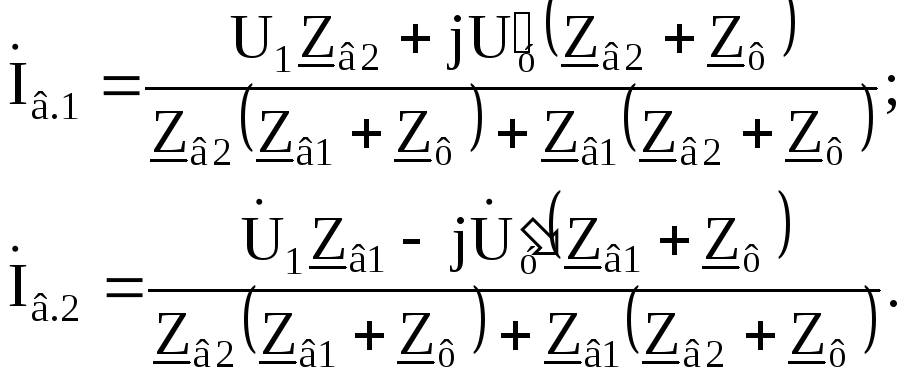 (2.5)
(2.5)
Симметричные составляющие тока ротора определяем, по схемам замещения рис. 2.8:
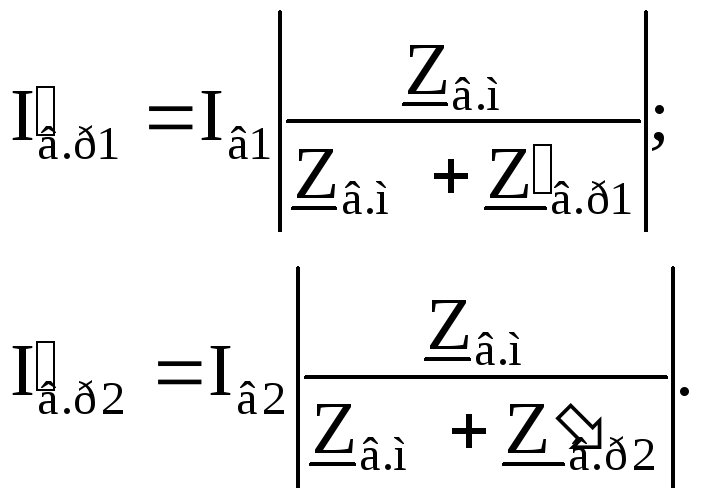 (2.6)
(2.6)
Как известно, электромагнитный вращающий момент M симметричного многофазного асинхронного двигателя при питании симметричной системой напряжений определяют по формуле
 , (2.7)
, (2.7)
где mс – число фаз статора; Iр' – ток ротора, приведенный к числу фаз и числу витков в обмотке статора; Rр' – активное сопротивление ротора, приведенное к числу фаз и числу витков в обмотке статора.
Формулу (2.7) можно использовать и для определения вращающих моментов прямой и обратной последовательностей исполнительного асинхронного микродвигателя, так как вращающиеся магнитные поля прямой и обратной последовательностей образованы симметричными системами токов.
Тогда в соответствии со схемами замещения (см. рис. 2.8) и выражениями (2.6) запишем уравнения для моментов прямой и обратной последовательностей:
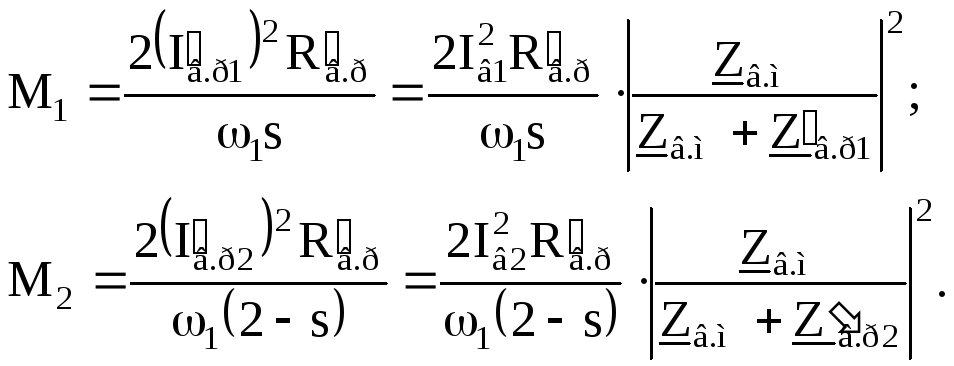 (2.8)
(2.8)
Результирующий вращающий момент равен разности моментов прямой и обратной последовательностей:
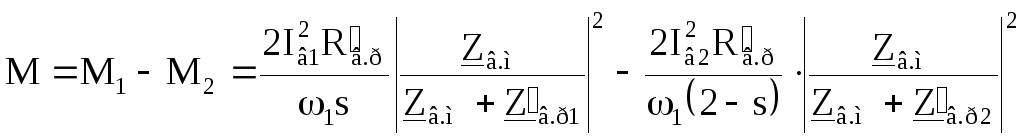 . (2.9)
. (2.9)
Вращающий момент, развиваемый двигателем при круговом поле, т. е. при Iв2 = 0 и Iв1 = Iв, с учетом (2.5)
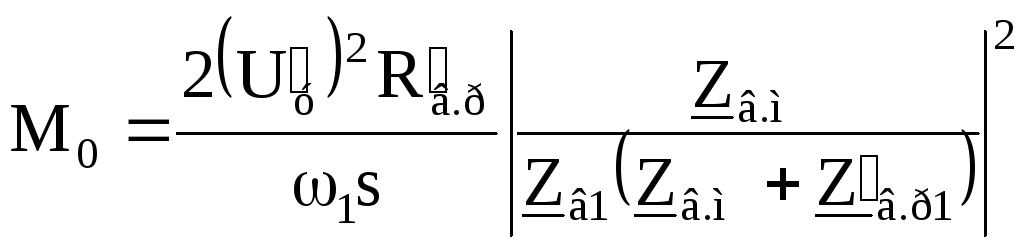 . (2.10)
. (2.10)
Пусковой момент при круговом поле Мп0 определяется по (2.10) при s = 1.
Анализ выражения (2.9) позволяет сделать следующие выводы:
при пульсирующем поле статора (Iв1 = Iв2) и скольжении s = 1 уменьшаемое и вычитаемое в правой части уравнения (2.9) равны, т.е. в этих условиях пусковой момент равен нулю;
при пульсирующем поле статора и s ≠ 1 уменьшаемое и вычитаемое в правой части уравнения (2.9) не равны (s ≠ 2 – s; Zв1 ≠ Zв2; Z'в.р1 ≠ Z'в.р2) и двигатель развивает момент прямого или обратного направления;
по мере изменения поля статора от пульсирующего до кругового происходит уменьшение M2 при одновременном увеличении M1 и соответственно рост результирующего вращающего момента M.
