
- •3. Упругие волны
- •3.1. Общие сведения о волновых пpоцессах
- •3.2. Уpавнение бегущей волны
- •3.3. Фазовая скорость. Волновое уравнение. Групповая скорость
- •Волновое уравнение–дифференциальное уравнение в частных производных, описывающее распространение волн в однородной изотропной среде. Для плоской волны оно имеет вид
- •3.4. Энеpгия волны
- •3.5. Стоячие волны
- •Вопросы и задания для самоконтроля, компьютерные упражнения
- •Задачи для самостоятельного решения
Вопросы и задания для самоконтроля, компьютерные упражнения
Какой процесс называют волновым? Чем он отличается от
колебаний?
Дать определение понятиям: волновое поле, фронт волны, волно-
вая поверхность, луч.
Верно ли утверждение: «Фронт волны – это движущаяся волновая поверхность»?
Какие волны называют продольными, поперечными? Приведите примеры.
Скорость каких волн больше, продольных или поперечных?
Продольными или поперечными будут волны, возбуждаемые смычком в струне, в воздухе?
Почему поперечные волны не распространяются в жидкостях и газах?
Могут ли упругие волны распространяться в вакууме? Ответ пояснить.
Найти разность фаз колебаний точек среды, расстояние между которыми равно: 1) /2; 2)/4; 3).
Выразить в длинах волн расстояние между двумя точками среды, колеблющимися в фазе; в противофазе.
11. К моменту времени tсферическая волна дошла до точки 4 (рис. 3. 16). Расстояние между сферами на рис. 3.16 равно/2. Указать точки среды, колеблющиеся в фазе, в противофазе. Показать волновые поверхности, фронт волны. Сравнить амплитуды.
12. Сравнить длину волны звуковых и ультразвуковых волн, если скорость распространения их в воздухе одинакова.
На рис. 3.17 представлен график поперечной волны. Найти фазы колебаний точек среды, имеющих в данный момент времени нулевые и максимальные смещения. Волна распространяется вправо.
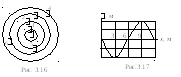
Записать в общем виде уравнение плоской бегущей волны и уравнение колебаний. Какие параметры у них общие? Чем они различаются ? Построить в общем виде их графики.
Как, зная уравнение волны, можно найти ее скорость?
Частота звука увеличилась вдвое, как изменилась энергия волны?
Амплитуда отраженной от преграды упругой волны составляет 0,8 амплитуды падающей. Как изменилась энергия отраженной волны в сравнении с падающей?
В какой среде при прочих равных условиях энергия звуковых волн больше: в камне или воде?
Как изменяются кинетическая, потенциальная, полная энергия: а) участка бегущей волны; б) гармонического осциллятора?
Чему равна разность фаз для потенциальной и кинетической энергии: а) участка бегущей волны; б) гармонического осциллятора?
Может ли в некоторый момент времени кинетическая энергия участка бегущей волны стать равной нулю? Каких значений достигают при этом потенциальная и полная энергии участка?
Могут ли для данного участка волны быть моменты времени, когда полная энергия равна нулю? Какими при этих условиях будут потенциальная и кинетическая энергии?
.Как образуется стоячая волна ? Чем она отличается от бегущей волны?
Почему фаза стоячей волны при переходе через узел меняется скачком на ?
Сравнить амплитуды и фазы точек среды, расположенных: а) на равных расстояниях от узла стоячей волны по разные его стороны; б) между соседними узлами на равных расстояниях от них.
В некоторый момент времени смещение точек среды в стоячей волне максимально. Изобразить графически стоячую волну через время Т/4; Т/2.
На рис. 3.12 представлена развертка стоячей волны во времени. Указать моменты времени, для которых полная энергия волны равна ее: а) потенциальной; б) кинетической энергии.
Есть ли в стоячей волне точки среды, энергия которых всегда равна нулю? Означает ли это исчезновение энергии?
Почему энергия не переносится через узлы?
Две волны, идущие навстречу друг другу, отличаются амплитудами. Будет ли такая волна переносить энергию?
Расстояние между соседними узлом и пучностью 3 м. Найти длину стоячей волны.
Объяснить отражение волны от границы раздела сред, пользуясь рис. 3.13, 3.14. Что означает выражение : «потеря полуволны» при отражении?
Граница раздела двух сред частично проницаема для волны, поэтому амплитуда отраженной волны за счет потери энергии при поглощении должна быть меньше амплитуды падающей. Если на границе раздела образуется узел, этого не происходит. Почему?
Компьютерные упражнения
Компьютерный тренажер по волновым процессам аналогичен тренажерам по механическим колебаниям
З
1. Длина волны = 62,5 см.
2. Период колебаний T = /, T = 1,56 с.
3. Частота = 1/T, =0,64 Гц.
4. Собственная циклическая частота = 2, = 1,28 с-1.
5. Волновое число k = 2/ , k = 0,032 м-1.
6. Амплитуда колебаний A = 95 с м.
7. Волновое уравнение , (х в см, время в с).
8. Уравнение волны = 95 cos(1,28t – 0.032x), см.
9. Смещения для точек 1 и 2 на графике:
 1
=-70см,
и 2
= 70 см.
1
=-70см,
и 2
= 70 см.
10. Hачальные фазы колебаний точек 1 и 2 можно опpеделить из уpавнения волны, подставляя в выpажение для фазы (t - kx) значения t = 0 и значения x: 24 см - для левой точки 1 и 55 см - для правой точки 2. После подстановки значений получим - 0,77 pад и - 1,76 pад для точек 1 и 2 соответственно. Колебания точек 1 и 2 по отношению к началу колебаний источника запаздывают по фазе.
Можно искать фазу колебаний графически: на длине волны фаза колебаний меняется на 2; расстояние х = разделено на 12,5 частей; в пределах каждой части фаза изменяется на 2/12,5.
11, 12. Уpавнения колебаний для выделенных точек:
1 = 95cos(1,28t –0,77) см - для точки1,
2 = 95cos(1,28 t – 1,76)) см - для точки 2.
13. Разность фаз колебаний pавна пpиблизительно pад, что определяется как вычислениями по формуле = 1-2. так и по графику: расстояние между точками составляет 6,25 частей, умножаем их на 2/12,5, получим разность фаз, равную , т.е. точки колеблются в протиивофазе.
З а д а н и е 2. Стоячая волна. Компьютерная модель «Стоячая волна» позволяет наблюдать в динамике образование поперечных стоячих волн при отражении от разных сред.
По графику стоячей волны (рис.3.19) определить параметры, перечисленные ниже. .
1 .
Длина бегущей волны
= 12 м.
.
Длина бегущей волны
= 12 м.
2. Амплитуды волн: бегущей Аб = 20 см, стоячей Аст = 40 см.
В стоячей волне на рис. 3.19 точки не достигли максимальных смещений.

3. Период колебаний Т = 0,04 с
4. Циклическая частота = 50 с-1.
5. Волновое число k = /6 м-1.
6. При отражении бегущей волны на границе раздела (справа) образуется узел, вид уравнения стоячей волны для данного момента времени определяется формулой (3.24) ст= 0,4sin(x/6)sin(50t) м;
7. Амплитуды колебаний точек с координатами х:
х, м : 0 1 2 3 4 5 6
Аст, см : 0 20 34,8 40 34,8 20 0
8. Уравнение колебаний точки А в стоячей волне для данного момента времени А 32sin(50t) cм.
9. Координаты узлов и пучностей вычисляем по формуле (3.25)
m0 1 2 3 4 …
ху, м 0 6 12 18 24 …
хп , м 3 9 15 21 27 …
10. Разность фаз для точек В и С, С и D: ВС = 0, CD = .
11. Координаты точек, в которых полная энергия стоячей волны равна нулю, соответствуют узлам.
