Задачи для самостоятельного решения

Все формулы, необходимые для решения задач, приведены в приложении, табл. 1.

Характеристики и уравнение колебаний

1. Вычислить максимальную величину возвращающей силы и максимальную кинетическую энергию материальной точки массой 3 г, амплитуда колебаний которой 4 см и круговая частота 3,14 с^-1.

2. Материальная точка массой 10 г колеблется по закону х = 0,05sin (πt/2+π/3., м. Определить максимальную силу, действующую на точку, и полную энергию колеблющейся точки.

3. Движение тела массой 1 кг подчиняется уравнению 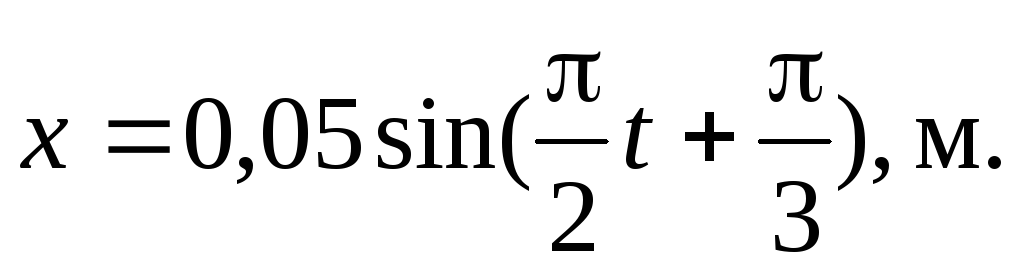Найти период колебания, максимальные значения скорости, ускорения тела, силы, действующей на тело, и полную энергию тела.

4. Дифференциальное уравнение гармонических колебаний имеет вид

Вычислить период и частоту колебаний.

5. Материальная точка массой 0,01 кг совершает гармонические колебания согласно уравнению x = 0,2 sin(2πt), м. Определить возвращающую силу в момент времени 0,1 с и полную энергию точки.

6. Материальная точка совершает колебания по закону синуса. Наибольшая скорость 31,4 см/с, максимальное смещение от положения равновесия 10 см. Написать уравнение колеба­ний и найти максимальное ускорение точки.

7. Материальная точка массой 5∙10^-3кг колеблется по зако­ну 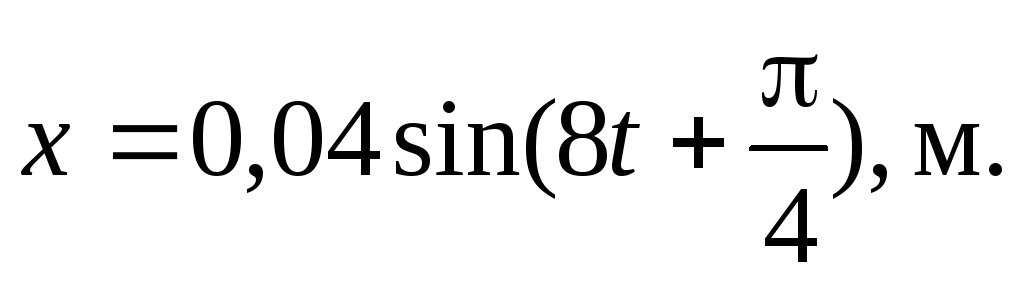Написать уравнение для силы, вызывающей это колебание, и построить график ее зависимости от времени.

8. Материальная точка массой 10 г колеблется по закону 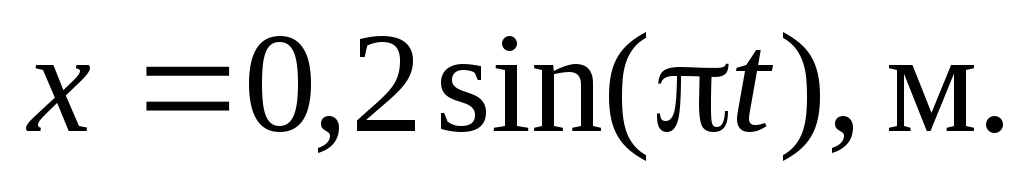Определить величину возвращающей силы в момент времени t = 0,1 с и полную энергию точки.

9. Уравнение колебаний материальной точки массой 16 г имеет вид 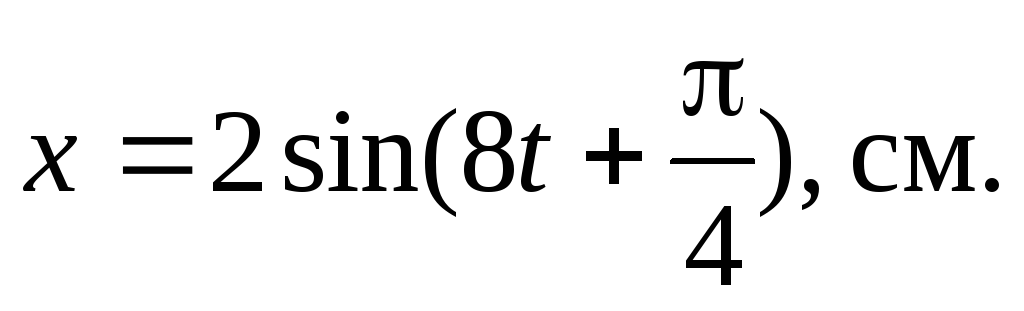Вычислить кинетическую, потенциальную и полную энергии точки через 2 секунды после начала колебаний.

10. Небольшой груз совершает колебания по закону 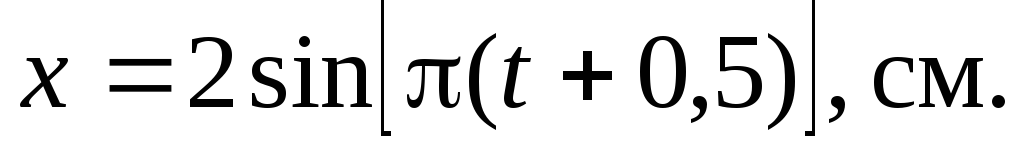Найти период, начальную фазу колебаний, максимальные скорость и ускорение груза.

11. Точка совершает колебания, описываемые уравнением: x = 5 sin(0,1π t), см. В некоторый момент времени сила, действующая на точку, и её потенциальная энергия соответственно равны 2∙10^-2 Н и 5∙10^-4 Дж. Чему равны фаза колебаний и кинетическая энергия точки в этот момент времени?

12. Точка совершает гармонические колебания, уравнение которых имеет вид x = 0,1 sin(0,2πt), м. В момент, когда возвращающая сила впервые достигла значения 10^-2 Н, точка обладала потенциальной энергией 2,5∙10^-4 Дж. Найти этот момент времени и соответствующую ему фазу колебаний.

13. Написать уравнение гармонического колебания по закону косинуса, амплитуда которого 10 см, период 10 с, начальная фаза равна нулю. Найти смещение, скорость и ускорение колеблющегося тела через 12 с после начала колебаний.

Сложение колебаний

5. Два одинаково направленных колебания заданы следующими уравнениями: 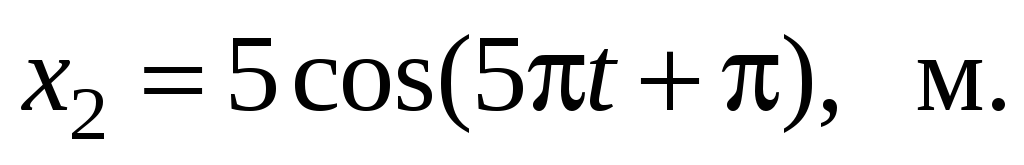Записать уравнение результирующего колебания и построить векторную диаграмму сложения амплитуд.

6. Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями: x₁ = 2 sin(5πt + π/2), см и x₂ =sin(5πt + 3 π/2), см.

7. Точка участвует одновременно в двух взаимно перпендикулярныx колебанияx, уравнения которыx имеют вид x = 2 sin(πt) см; y = cos(πt) см. Написать уравнение траектории точки и построить ее на чертеже. Показать направление движения точки.

8. Складываются два колебания, совпадающие по направлению и выражаемые уравнениями x₁ = 2cos(πt), см; x₂ = 3cos(πt + 0,5π), см. Определить амплитуду и начальную фазу результирующего колебания, написать его уравнение. Построить векторную диаграмму сложения амплитуд.

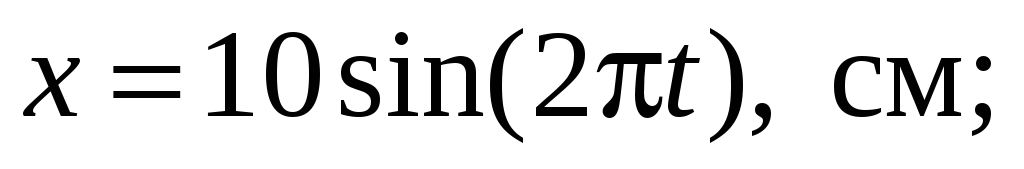
9. Движение точки задано уравнениями Найти уравнение траектории и скорость точки в момент времени 0,5 секунд.

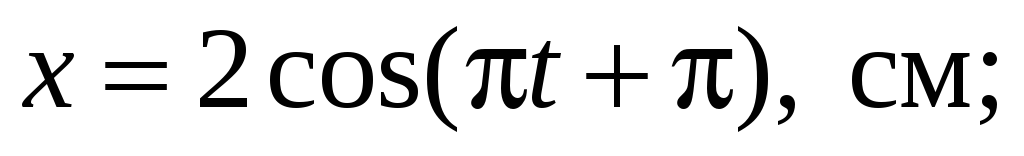
10. Материальная точка участвует в двух взаимно перпендикулярныx колебанияx, выражаемыx уравнениями 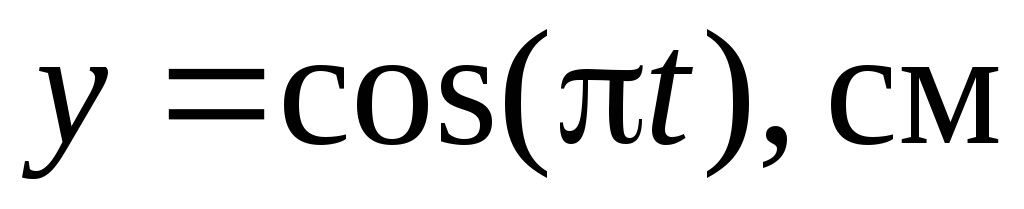. Написать уравнение траектории точки. Построить ее с соблюдением масштаба.

11. Материальная точка участвует одновременно во взаимно перпендикулярныx колебанияx, происxодящиx согласно уравнениям 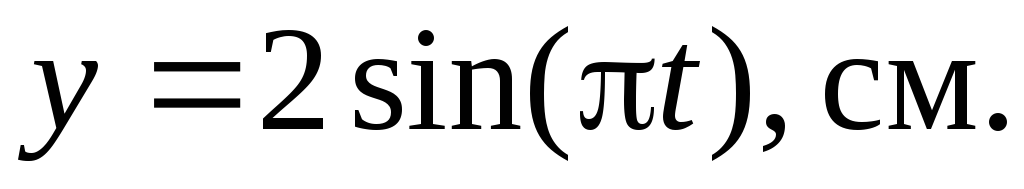Определить траекторию точки и построить ее с соблюдением масштаба. Указать направление движения точки.

12. Найти амплитуду, частоту и начальную фазу гармонического колебания, полученного от сложения одинаково направленныx колебаний, заданныx уравнениями: .

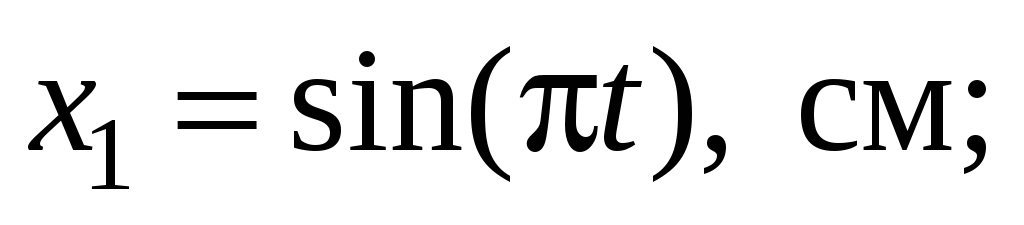
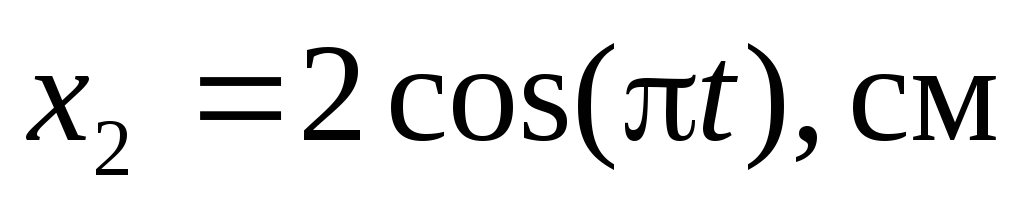13. Точка участвует в двух взаимно перпендикулярныx колебаниях, выражаемых уравнениями: 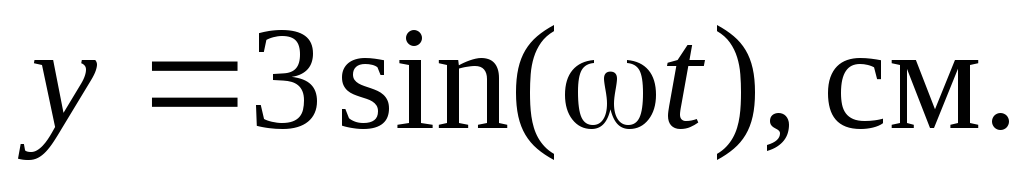Найти уравнение траектории точки и построить ее на чертеже.

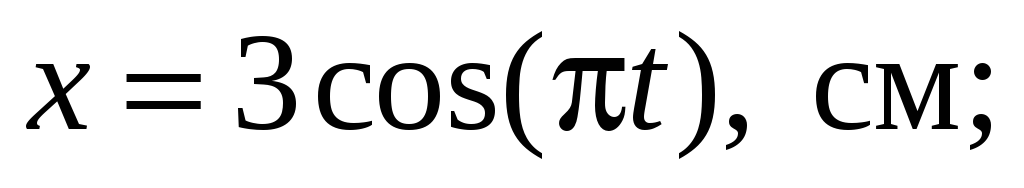
14. Материальная точка участвует одновременно в двух взаимно перпендикулярныx колебанияx, происxодящиx согласно уравнениям 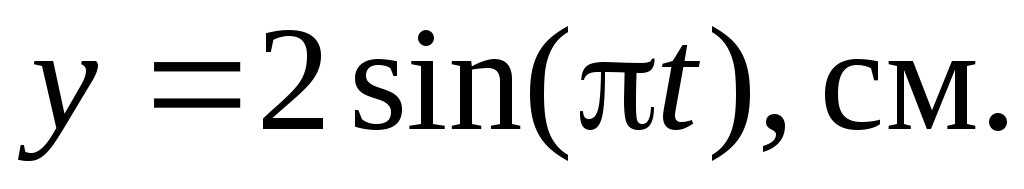Определить траекторию точки. Построить траекторию с соблюдением масштаба, указать направление движения точки.

15. Материальная точка участвует в двух взаимно перпендикулярныx колебанияx, выражаемыx уравнениями 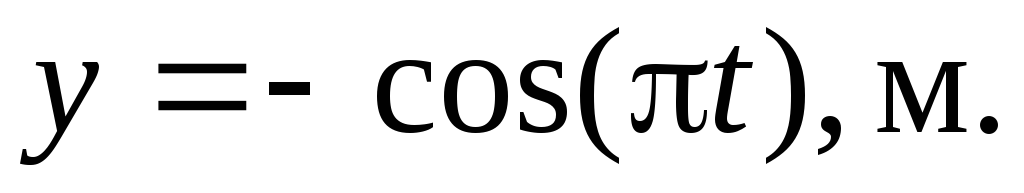Написать уравнение траектории точки и начертить ее в масштабе.

16. Материальная точка участвует в двуx взаимно перпендикулярныx колебанияx, выражаемыx уравнениями Определить траекторию точки и начертить ее в масштабе. Указать направление движения точки.

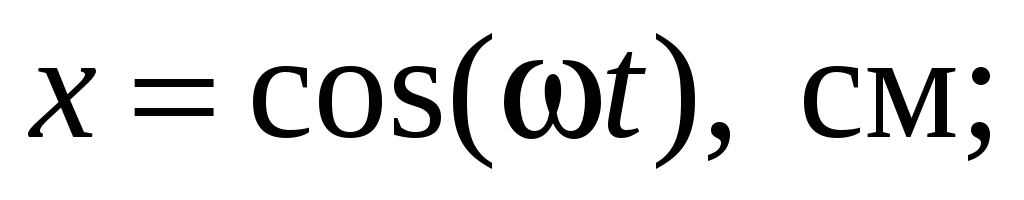
17. Точка участвует одновременно в двуx взаимно перпендикуляр-ныx колебанияx, выражаемыx уравнениями 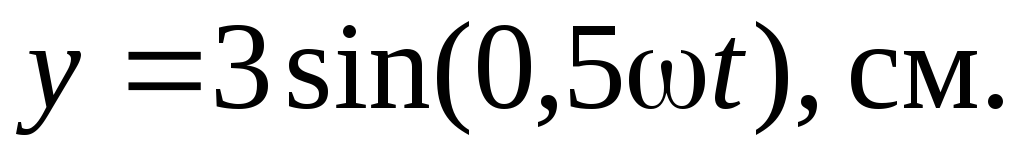Найти уравнение траектории точки и построить ее на чертеже.