1.40 Примеры вычислений потенциальной энергии. Полная энергия________________

Конкретный вид функции П зависит от характера силового поля.

Потенциальная энергия тела массой т на высоте h_________________________________________________

Это выражение вытекает из того, что потенциальная энергия равна ра­боте силы тяжести при падении тела с высотыh на поверхность Земли.

Высота Л отсчитывается от нулевого уровня, для которого П₀ = 0, g — ускорение свободного падения.

Поскольку начало отсчета выбирается произвольно 1.38, то потенциаль­ная энергия может иметь отрицательное значение (кинетическая энер­гия всегда положительна!). Если принять за нуль потенциальную энер­гию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина Л'), П = -mgh'.

Потенциальная энергия упруго деформированного тела (пружины)___________________________________

Это выражение получается из того, что работа силы при деформации пружины идет на увеличение потенциальной энергии пружины.

Элементарная работа dA, совершаемая силой F_x при бесконечно ма­лой деформации dx, dA = F_x dx = kx dx (F_x = -F _{x упр} = -(-kx) = kx).

Полная работа .

[k — коэффициент упругости (для пружины — жесткость); F_{х упр} =- kx - проекция силы упругости на ось х; F_{х упр} направлена в сторону, противопо­ложную деформации x. По третьему закону Ньютона деформирующая сила равна по модулю силе упругости и противоположно ей направлена]

Полная механическая энергия системы___

Энергия механического движения и взаимодействия, т. е. равна сумме кинетической и потенциальной энергий.

1.3.3. Закон сохранения энергии

1.41 Закон сохранения механической энергии_

Исходные данные_____________________________________________________________________________________________

Рассматривается система материальных точек массами т₁, т₂, ... , т_п, движущихся со скоростями .

Второй закон Ньютона для каждой из материальных точек________________________________________________________

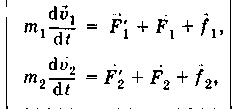[ — равнодействующие внутренних консерватив­ных сил, действующих на каждую из этих точек;

—равнодействующие внешних сил, которые счита­ются консервативными;

—равнодействующие внешних неконсервативных сил, действующие на каждую из материальных точек]

Учет перемещений точек под действием сил_____________________________________________________________________

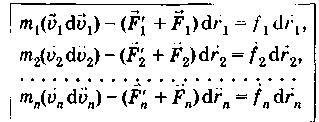Точки движутся под действием сил, поэтому за вре­мя dt совершают перемещения . Каждое уравнение второго закона Ньютона умноже­но скалярно на соответствующее перемещение, и уч­тено, что.

После сложения уравнений

Правая часть равенства определяет работу внешних неконсервативных сил, действующих на систему.

Элементарное приращение кинетической энергии__________________________________________________________________

Первый член равенства (*) равен элементарному при­ращению кинетической энергии dT системы 1.37.

Элементарное приращение потенциальной энергии системы________________________________________________________

Второй член равенства (*) равен элементарной работе внутрен­них и внешних консервативных сил, взятой со знаком «ми­нус», т. е. равен элементарному приращению потенциальной энергии dП системы 1.39.

Изменение полной механической энергии системы___________________________________________________________________

Равно работе внешних неконсервативных сил, действующих на систему.

Правая часть равенства (*) задает dA.

В случае отсутствия внешних неконсервативных сил

Из записанного равенства следует, чтоТ + П = Е = const.