1.7.4. Импульс и энергия материальной точки в релятивистской динамике

Релятивистский импульс и закон его сохранения_

Релятивистский импульс____Совпадает по направлению со скоростью , с которой движется ма­териальная точка массойт.

При V « с (точнее, в пределе при с —► ∞) выражение релятивист­ского импульса совпадает с формулой для импульса в клас­сической механике .Закон сохранения релятивистского импульса________________________________________________________________

Релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Этот закон — следствие однородности пространства .

Основной закон релятивистской механики_____

Основной закон релятивистской механики

Э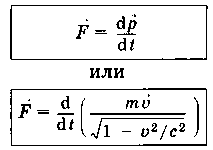то уравнениеинвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяетпринципу относи­тельности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. ПриV<<с приходим к классическому закону Ньютона1.20.

[— релятивистский импульс материальной точки]

♦ Если на материальную точку одновременно действуют несколько сил, то в формуле основного закона релятивистской динамики — равнодей­ствующая всех приложенных сил.

Условие применимости законов классической механики__________________________

Из приведенных формул 1.83—1.90следует, что при скоростях, значитель­но меньших с, они переходят в формулы классической механики. Следо­вательно, условием применимости законов классической (ньютоновской) механики является условиеV« с. Законы классической механики полу­чаются как следствие теории относительности для предельного случаяV« с (формально переход осуществляется при с —► ∞). Таким образом,классическая механика —это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).

1.91 Энергия в релятивистской динамике_________________________________________

Кинетическая энергия в релятивистской динамике_________________________________________________

Элементарная работа силы на малом перемещении1.35

(учли основной закон релятивист­ской динамики).

Тогда

Приращение кинетической энергии материальной точки на элементар­ном перемещении равно элементарной работе на том же перемещении: dT = dA 1.37,

откуда и получается записанное выражение.

♦ Разлагая (1 - V²/c²), получаем , т. е. приV « c

выражение для кинетической энергии в релятивистской динамике

совпадает с обычным выражением для кинетической энергии в классиче­ской механике.

Полная энергия релятивистской частицы (закон взаимосвязи массы и энергии)__________________________________

Полная энергия в разных системах отсчета различна.

[т — масса частицы; V — ее скорость; с — скорость распространения света в вакууме]

Закон сохранения энергии в релятивистской механике______________________________________________

Полная энергия замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Этот закон — следствие однородности времени 1.41.

Энергия покоя__________________________________________________________________________________

Энергия покоящейся частицы (тела) (приV = 0).

Значения т иЕ₀ не зависят от выбора инерциальной системы отсчета.

Классическая механика энергию покоя E₀не учитывает; считают, что приV = 0 энергия покоящегося тела равна нулю.