Уравнение динамики вращательного движения твердого тела

Исходные данные для вычисления работы при вращении тела

Сила приложена к точке В, находящейся от оси на расстоянии r, α — угол между направлением силы и радиусом-вектором . Так как тело абсо­лютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.

Работа при вращении тела

При повороте тела на бесконечно малый угол dφ точка В силы проходит путь rdφ и работа равна произведению проекции силы на направление смещения на величину смещения: d А = F sin α·r·dφ. Учитывая, что М_z = F·r· sin α = F·l 1.53, получаем dA = М_г dφ.

Уравнение динамики вращательного движения твердого тела

Момент сил твердого тела относительно оси равен произведению момента инерции относительно той же оси на угловое ускорение.

Работа вращения тела идет на увеличение его кинетической энергии:

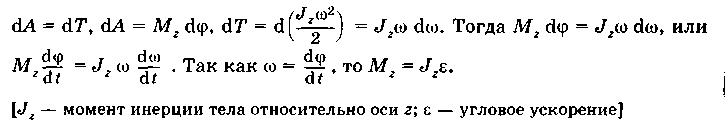
МОМЕНТ ИМПУЛЬСА И ЗАКОН ЕГО СОХРАНЕНИЯ

Момент импульса__

Момент импульса материальной точки относительно неподвижной точки О__

Физическая величина, определяемая векторным произведением радиус-вектора, материальной точки, проведен­ного из точкиО, на импульс , этой матери­альной точки.

—псевдовектор, его направление совпадает с направлением поступательного движения право­го винта при его вращении от , к

Модуль вектора момента импульса__

[a — угол между векторами г, и Д.; / = г sin a — плечо импульса. Перпендикуляр опущен из точки О на пря­мую, вдоль которой направлен импульс частицы]

Момент импульса материальной точки относительно неподвижной оси z__

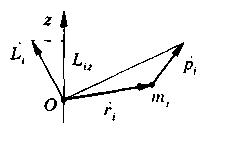Скалярная величина L_iz, равная проекции на эту ось вектора момента импульса, определенного от­носительно произвольной точки О данной оси г.

Значение момента импульса L_u не зависит от по­ложения точки О на оси г.

Деформация твердого тела

Закон Гука.

Потенциальная энергия упруго растянутого стержня_

Напряжение

Сила, действующая на единицу площади поперечного сечения тела.

Если сила направлена по нормали к поверхности, то напряжение называ­ ется нормальным если же по касательной к поверхности; — тангенци­альным.

Опытный факт, установленный Гуком______________________________

Для малых деформаций относительное удлинение ε и напряжение σ пря­ мо пропорциональны друг другу.

Модуль Юнга_______________________________________________________

Определяется напряжением, вызывающим относительное удлинение, равное единице.

Закон Гука__________________________________________________________

Абсолютное удлинениетела при упругой деформации пропорцио­ нально действующей на тело силе.

Записав , получим(k — коэффициент пропорциональности).

♦ Закон Гука выполняется только для упругих деформаций.

Потенциальная энергия упруго растянутого (сжатого) стержня_________

Равна работе, совершаемой внешними силами при деформации:

Если х — абсолютное удлинение стержня, изменяющееся в процессе

деформации от 0 до , то, согласно закону Гука,F = kx =. Тогда

пропорциональна квадрату деформации .

♦ В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходя­щим деформациям растяжения или сжатия и сдвига.