1.33 Закон сохранения импульса_______________________________________________

Исходные данные___________________________________________________________________________

Рассматривается механическая система из п тел, масса и скорость кото­рых соответственно равны m₁ , m₂ , ... , m_n и .

Второй закон Ньютона для каждого из п тел механической системы________________________________

[ — равнодействующие внутренних сил, действую­щих на каждое тело механической системы; — равно­действующие внешних сил, действующих на каждое тело механи­ческой системы]

После почленного сложения уравнений________________________________________________________

Производная по времени от импульса механической систе­мы равна геометрической сумме внешних сил, действующих на систему.

Учли, что — импульс системы, а геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю.

В случае замкнутой системы

Внешние силы отсутствуют (или геометрическая сумма всех внешних сил равна нулю).

Закон сохранения импульса____________________________________________________________________

Импульс замкнутой системы сохраняется, т. е. не изменяет­ся с течением времени.

Этот закон — фундаментальный закон природы (он универ­сален).

Закон сохранения импульса — следствие однородности пространства_________________________________

Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.

♦ Импульс сохраняется и для незамкнутой системы, если геометрическая сум­ма внешних сил равна нулю.

1.34Закон движения центра масс_________________________________________________

Центр масс системы материальных точек (тела)_________________________________________________

Воображаемая точка С, положение которой характеризует распределе­ние массы этой системы (тела).

Для определения положения центра масс достаточно поочередно подве­сить тело за две различные точки на его поверхности и провести через точки подвеса вертикали, пересечение которых и даст положение центра масс (центр масс может располагаться вне тела).

Радиус-вектор центра масс__

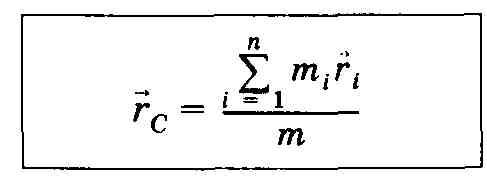[m_i и — соответственно масса и радиус-векторi-й материальной точки; п — число материальных точек в системе; — масса системы]

Скорость центра масс__

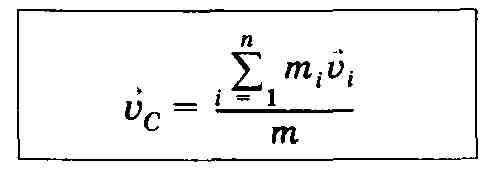
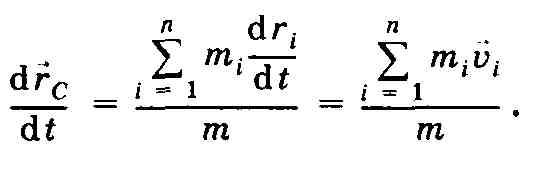
Учли, что =

Импульс системы материальных точек__

Равен произведению массы системы на скорость ее центра массP_i = m_iv_i; p = Zp_t.

Закон движения центра масс_

Центр масс системы движется как материальная точка, в ко­торой сосредоточена масса всей системы и на которую дейст­вует сила, равная геометрической сумме всех внешних сил, приложенных к системе

Работа и энергия энергия, работа, мощность Энергия. Работа силы_

Энергия - Универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные виды энергии — механическую, тепловую, электромагнитную, ядерную и др.

Работа силы - Количественная характеристика процесса обмена энергией между взаимодействующими телами.

Работа постоянной силы F, составляющей угол α с направлением прямолинейного движения тела

Работа этой силы равна произведе­нию проекции силы F_s на направ­ление перемещения (F_s = F cos α), умноженной на перемещение точ­ки приложения силы.

Элементарная работа силы на перемещении

[α — угол между векторами и ;ds = || — элементарный путь; F_s — проекция вектора на вектор ]

♦ Работа — величина скалярная.

25

Работа силы на участке траектории 1—2_

Для вычисления этого интеграла надо знать зависимость F_s от s вдоль траектории 1—2 (пример на ри­сунке).

Геометрический смысл выраже­ния для А: искомая работа опреде­ляется на графике площадью за­крашенной фигуры.

Единица работы___________________________________________________________________________

1 джоуль — работа, совершаемая силой, равной 1 Н на пути 1 м.

Мощность

Мощность_

Физическая величина, характеризующая скорость совершения работы.

Мощность, развиваемая силой F

Равна скалярному произведению вектора силы на вектор скорости, с ко­торой движется точка приложения этой силы.

За время dt сила совершает работу , и мощность, развиваемая этой

силой, в данный момент времени равна

♦Мощность — величина скалярная.

Единица мощности

1 ватт — мощность, при которой за время 1 с совер­шается работа 1 Д