1.2.4. Неинерциальные системы отсчета. Силы инерции

1.25 Силы инерции и их проявление

Силы инерции

Силы, обусловленные ускоренным движением системы отсчета относи­тельно измеряемой системы отсчета.

Силы инерции вызываются не взаимодействием тел, а ускоренным дви­жением системы отсчета. Поэтому они не подчиняются третьему зако­ну Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу.

О втором законе Ньютона в неинерциальных системах отсчета

В неинерциальных системах отсчета 1,18 законы Ньютона, вообще гово­ря, несправедливы. Если же кроме сил, обусловленных взаимодействием тел друг на друга, рассмотреть и силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета.

Второй закон Ньютона для неинерциальных систем отсчета

Произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил (включая и силы инерции), действую­щих на данное тело.

Силы инерции должны быть такими, чтобы вместе с силамиF, обусловленными воздействием тел друг на друга, они сообщали телу ускорение , каким оно обладает в неинерциальных системах отсчета ( — ускорение тела в инерциальной системе отсчета)).

Три возможных проявления сил инерции________________________________________________________

Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, поэтому в общем случае нужно учитывать следующие случаи проявления этих сил:

• Силы инерции при ускоренном поступательном движении системы отсчета.

• Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета.

1. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета.

65535. 1.26 Силы инерции

при ускоренном поступательном движении системы отсчета__________________

Т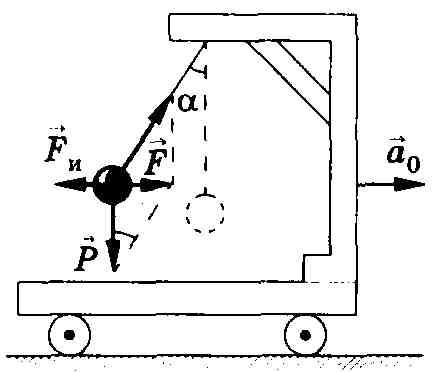ележка покоится или движется равномерно и прямолинейно (опыт)

Нить, удерживающая шарик, вертикальна, и си­ла тяжести Р уравновешивается силой реакции нити .

Тележка движется равномерно и прямолинейно (опыт)

Нить начнет отклоняться от вертикали назад до такого угла а, пока результирующая сила не обеспечит ускорение шарика, рав­ное .

Инерциальная система отсчета

(анализ опытных данных)______________________________________________________________________

В системе отсчета, связанной, например, с помещением, на шарик дейст­вует результирующая сила , направленная в сторону ускорения тележ­ки а₀, и для установившегося движения шарика (шарик теперь движется вместе с тележкой с ускорением а₀) равна F = mg tg а = ma₀, откуда (тем больше, чем больше ускорение тележки).

Неинерциальная система отсчета

(анализ опытных данных)_______________________________________________________________________

В системе отсчета, связанной с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила уравновешивается равной и про­тивоположно направленной ей силой F_u, которая является не чем иным, как силой инерции, так как на шарик никакие другие силы не дейст­вуют. .

Примеры проявления сил инерции. Когда поезд набирает скорость, то пасса­жир, сидящий по ходу поезда, под действием силы инерции прижимается к спинке сиденья. Наоборот, при торможении поезда сила инерции направлена в противоположную сторону и пассажир удаляется от спинки сиденья. Особенно эти силы заметны при внезапном торможении поезда. Силы инерции проявляют­ся в виде перегрузок, которые возникают при запуске и торможении космиче­ских кораблей.

Силы инерции, действующие на тело,

покоящееся во вращающейся системе отсчета_______________________________

Диск вращается вокруг вертикальной оси с угловой скоростью (опыт)

Н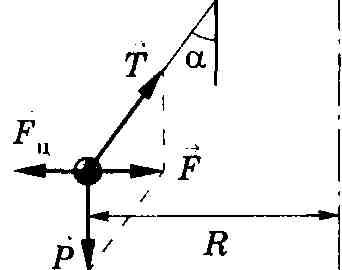а диске, на разных расстояниях от оси вращения установлены ма­ятники (на нитях подвешены ша­рики массойm). При вращении диска маятники отклоняются от вертикали на некоторый угол а.

Инерциальная система отсчета

(анализ данных)__________________________________________________________________________________

В системе отсчета, связанной, например, с помещением, шарик равно­мерно вращается по окружности радиусом R (расстояние от центра вра­щающегося шарика до оси вращения). Следовательно, на него действует сила, равная F = m ω²R и направленная перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести и силы натяжения нити. Для установившегося движения шарика, откуда tg= ω² R/g (тем больше, чем больше R и ω).

Неинерциальная система отсчета

(анализ данных)__________________________________________________________________________________

В системе отсчета, связанной с вращающимся диском, шарик покоится, что возможно, если сила уравновешивается равной и противоположно направленной ей силой , которая является не чем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Сила F_ц, называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска, F_ц = -m·ω²R.

Примеры проявления сил инерции. Действию центробежных сил инерции под­вергаются, например, пассажиры в движущемся транспорте на поворотах, лет­чики при выполнении фигур высшего пилотажа. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов и т. д.) принимаются специальные меры для уравновешивания центробежных сил инерции.

♦ Центробежная сила инерции (F_ц = -m·ω²R) не зависит от скорости тел относи­тельно вращающихся систем отсчета, т. е. действует на все тела, удаленные от оси вращения на конечное расстояние, независимо от того, покоятся ли они в этой системе или движутся относительно нее с какой-то скоростью.