1.2.3. Принцип относительности галилея

1.23 Преобразования координат Галилея______________

Исходные данные______________________________________________________________________________

Р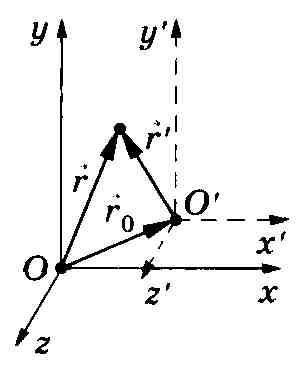ассматривают две системы отсчета: инерциальную сис­тему отсчетаК (с координатами х, у, z), условно считая ее неподвижной, и систему К' (с координатами х', у', z'), движущуюся относительно К равномерно и прямоли­нейно со скоростью ( = const). Отсчет времени — с мо­мента, когда начала координат обеих систем совпадают. На рисунке показано расположение систем в произволь­ный момент времени t. Скорость направлена вдоль ОО'; .

Преобразования координат Галилея_____________________________________________________________

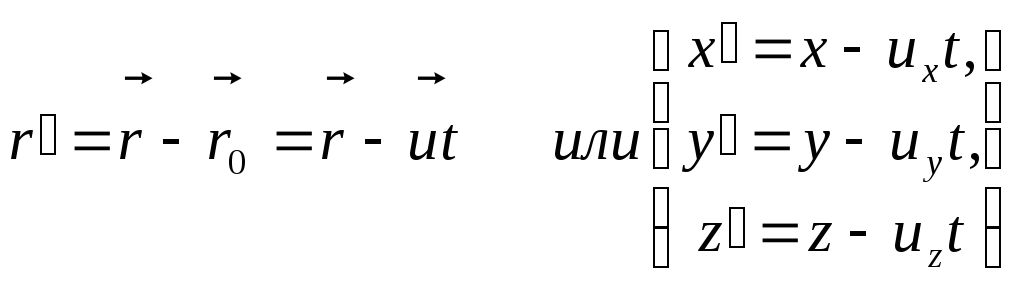
Задают связь между радиусами-векторами или координатами произвольной точки А в обеих системах.

Частный случай преобразований Галилея________________________________________________________

x' = x - vt,

y' = y,

z' = z

Система К' движется со скоростью вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают).

В классической механике считается, что ход времени не зависит от отно­сительного движения сиcтем отсчета, т. е. к преобразованиям Галилея добавляют уравнение t' = t.

1.24 Принцип относительности Галилея _________________________________________

Формулировки принципа относительности Галилея_______________________________________________

Законы динамики одинаковы во всех инерциальных системах отсчета.

Все инерциальные системы отсчета по своим механическим свойствам эквивалентны друг другу.

Правило сложения скоростей в классической механике_______________________________________________

Продифференцировав по времени и учитывая, чтоt' = t 1.23,

получим .

[ — скорость движения системы К' относительно системы К 1.23; и — со­ ответственно скорости в системах К и К']

Подтверждение принципа относительности Галилея

(механического принципа относительности)_______________________________________________________

В системе К ускорение . Следовательно, если на точку А другие тела не действуют (= 0), тоа' = 0, т. е. системаК' является инерциальной (точка движется относительно нее равномерно и прямолинейно или покоится).

Из равенства а' = а вытекает подтверждение принципа относительности Галилея (механического принципа относительности): уравнения дина­мики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.

е. являются инвариантными по отношению к преобра­зованиям координат.

Никакими механическими опытами, проводимыми внутри данной инер­циальной системы отсчета, нельзя установить, покоится она или движет­ся равномерно и прямолинейно. Во всех инерциальных системах отсчета одинаковы свойства пространства и времени, одинаковы и все законы механики.