
- •Основы динамики поступательного движения
- •1.2.1. Инерциальные системы отсчета. Масса и импульс тела. Сила
- •1.18 Первый закон Ньютона________________________________________________________________
- •Неинерциальная система отсчета_________
- •1.19 Масса и импульс тела. Сила_______________________________________________
- •1.2.2. Второй и третий законы ньютона
- •1.20 Основной закон динамики________________________________________________________
- •1.21 1.21 Принцип независимости действия сил______________________________________
- •1.22 Третий закон Ньютона_______
- •1.2.3. Принцип относительности галилея
- •1.23 Преобразования координат Галилея______________
- •1.24 Принцип относительности Галилея _________________________________________
- •1.2.4. Неинерциальные системы отсчета. Силы инерции
- •1.26 Силы инерции
- •1.28 Силы инерции, действующие на тело,
- •1.29 Основной закон динамики для неинерциальных систем отсчета _________________
- •1.2.5. Силы трения
- •1.30 Виды трения___________________________________________________________________
- •1.33 Закон сохранения импульса_______________________________________________
- •1.34Закон движения центра масс_________________________________________________
- •Скорость центра масс__
- •Работа и энергия энергия, работа, мощность Энергия. Работа силы_
- •Кинетическая и потенциальная энергия
- •1.38 Консервативная и диссипативная силы_____________________________________
- •1.39 3 Потенциальная энергия и консервативные силы_____________________________
- •1.40 Примеры вычислений потенциальной энергии. Полная энергия________________
- •1.3.3. Закон сохранения энергии
- •1.41 Закон сохранения механической энергии_
- •Закон сохранения механической энергии
- •1.42 Консервативные системы и закон сохранения энергии_ Консервативные системы
- •1.43 Закон сохранения и превращения энергии_____________________________________
- •1.3.4. Графическое представление энергии
- •1.44 Потенциальные кривые и их анализ на некоторых примерах____________________
- •Анализ потенциальной кривой для упругодеформированного тела
- •1.45 Анализ потенциальной кривой (общий случай)
- •1.3.5. Удар абсолютно упругих и неупругих тел
- •1.46 Общие понятия_______________
- •1.47 Центральный абсолютно упругий удар____________________________
- •1.48 Центральный абсолютно неупругий удар______________________________________
- •Динамика вращательного движения
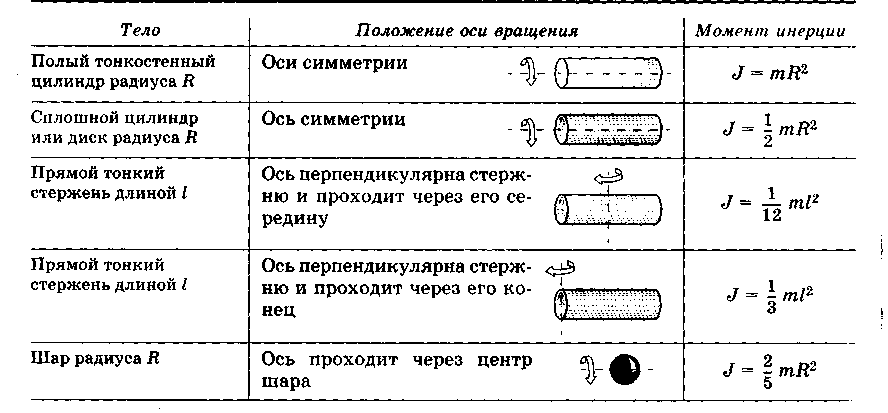
- •Моменты инерции однородных тел
- •1.52 Кинетическая энергия вращающегося твердого тела_______
- •Момент силы. Уравнение динамики вращательного движения твердого тела Момент силы__
- •Уравнение динамики вращательного движения твердого тела
- •1.7. Элементы релятивистской механики
- •1.7.4. Импульс и энергия материальной точки в релятивистской динамике
- •1.91 Энергия в релятивистской динамике_________________________________________
- •1.92 Связь между энергией и импульсом
Динамика вращательного движения
МОМЕНТ ИНЕРЦИИ. КИНЕМАТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩЕНИЯ
Определение момента инерции_
Момент инерции тела относительно неподвижной оси___
Ф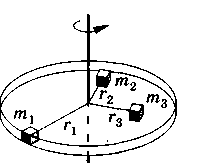
![]() изическая
величина, равная сумме произведений
элементарных масс на квадраты их
расстояний до рассматриваемой оси.
Суммирование производится по всем
элементарным массамтi
на которые можно разбить тело.
изическая
величина, равная сумме произведений
элементарных масс на квадраты их
расстояний до рассматриваемой оси.
Суммирование производится по всем
элементарным массамтi
на которые можно разбить тело.
Момент инерции — величина аддитивная: момент инерции тела равен сумме моментов инерции его частей.
Момент инерции тела в случае непрерывного распределения масс_
![]() Интегралы
берутся по всему объему тела, причем
величины p
и r
являются функциями точки (например,
декартовых координат x,
y
и z).
Интегралы
берутся по всему объему тела, причем
величины p
и r
являются функциями точки (например,
декартовых координат x,
y
и z).
[p — плотность тела в данной точке; dm = р dV — масса малого элемента тела объемом dV, отстоящего относительно оси вращения на расстоянии r;]
Момент инерции сплошного цилиндра. Теорема Штейнера_
Момент инерции однородного сплошного цилиндра радиуса R относительно егогеометрической оси_

![]() Разобьем цилиндр на отдельные полые
концентрические цилиндры
бесконечно малой толщиныdr
с внутренним радиусомr
и внешнимr +dr.
Момент инерции каждого полого
цилиндраdJ =r2
dm (dr<<r), объем элементарного
цилиндра2πrh·
dr, его массаdm
=2πrhp· dr
иdJ =2πhpr3·
dr (p— плотность материала). Момент инерции
сплошного цилиндра
Разобьем цилиндр на отдельные полые
концентрические цилиндры
бесконечно малой толщиныdr
с внутренним радиусомr
и внешнимr +dr.
Момент инерции каждого полого
цилиндраdJ =r2
dm (dr<<r), объем элементарного
цилиндра2πrh·
dr, его массаdm
=2πrhp· dr
иdJ =2πhpr3·
dr (p— плотность материала). Момент инерции
сплошного цилиндра
![]() .
.
Поскольку πR2h— объем цилиндра, его массат =
πR2hp,
а![]() .
.
Теорема Штейнера_
J = JC+ та2
Момент инерции тела J относительно любой оси вращения равен моменту его инерцииJс относительно параллельной оси, проходящей через центр массС тела, сложенному с произведением массыт тела на квадрат расстоянияа между осями.
Моменты инерции однородных тел
1.52 Кинетическая энергия вращающегося твердого тела_______
Исходные данные____
 Тело
вращается вокруг неподвижной осиz.
Мысленно разбиваем это тело на
элементарные массыm1,т2, ... ,mi,
... , находящиеся от оси на расстоянияхr1,r2,
... ,ri,
... . При вращении твердого тела
элементарные объемы массамиmi,
опишут окружности различных радиусовri.
Тело
вращается вокруг неподвижной осиz.
Мысленно разбиваем это тело на
элементарные массыm1,т2, ... ,mi,
... , находящиеся от оси на расстоянияхr1,r2,
... ,ri,
... . При вращении твердого тела
элементарные объемы массамиmi,
опишут окружности различных радиусовri.
Кинетическая энергия i-й элементарной массы
![]() Линейная
скорость элементарной массы ш1
равна vt
= cor-
(угловая скорость вращения всех
элементарных объемов одинакова).
Линейная
скорость элементарной массы ш1
равна vt
= cor-
(угловая скорость вращения всех
элементарных объемов одинакова).
Кинетическая энергия вращающегося твердого тела
![]()
(учли, что
![]() );Jz
– момент инерции тела относительно
осиz.
);Jz
– момент инерции тела относительно
осиz.
Из сравнения формул
![]() и
и![]() следует,
чтомомент инерции – мера инертности
тела при вращательном движении.
следует,
чтомомент инерции – мера инертности
тела при вращательном движении.
Кинетическая энергия тела при плоском движении
![]() Складывается
из энергии поступательного движения
со скоростью, равной скорости центра
масс, и энергии вращения вокруг оси,
проходящей через центр масс тела.
Складывается
из энергии поступательного движения
со скоростью, равной скорости центра
масс, и энергии вращения вокруг оси,
проходящей через центр масс тела.
[т — масса тела; VC — скорость центра масс тела; JC — момент инерции тела относительно оси, проходящей через его центр масс; ω — угловая скорость тела]
Момент силы. Уравнение динамики вращательного движения твердого тела Момент силы__
Момент силы относительно неподвижной точки О__
Ф![]()
 изическая
величина, определяемая векторным
произведением радиуса-вектора
изическая
величина, определяемая векторным
произведением радиуса-вектора![]() ,
проведенного
из точки О в
точку А
приложения
силы, на силу
,
проведенного
из точки О в
точку А
приложения
силы, на силу
![]() .
.
![]() —псевдовектор,
его направление
совпадает с направлением поступательного
движения правого винта при его
вращении от
—псевдовектор,
его направление
совпадает с направлением поступательного
движения правого винта при его
вращении от
![]() к
к
![]() .
.
Модуль вектора момента силы_
[![]() а— угол между
а— угол между
![]() и
и![]() ;
;
![]() — кратчайшее
расстояние между линией действия силы
и точкой О — плечо
силы]
— кратчайшее
расстояние между линией действия силы
и точкой О — плечо
силы]
Момент силы относительно неподвижной оси z_
С
![]() калярнаявеличина
Мг,
равная
проекции на эту ось вектора М
момента
силы, определенного относительно
произвольной точки О данной оси г.
Значение
момента Мz
не зависит
от выбора положения точки О
на оси z.
калярнаявеличина
Мг,
равная
проекции на эту ось вектора М
момента
силы, определенного относительно
произвольной точки О данной оси г.
Значение
момента Мz
не зависит
от выбора положения точки О
на оси z.
Если ось z
совпадает
с направлением вектора
![]() ,
то момент силы представляется в виде
вектора, совпадающего с осью.
,
то момент силы представляется в виде
вектора, совпадающего с осью.
