
МІНІСТЕРСТВО ОСВІТИ І НАУКИ
ХМЕЛЬНИЦЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
Кафедра прикладної математики та соціальної інформатики
КУРСОВИЙ РОБОТА
ПОЯСНЮВАЛЬНА ЗАПИСКА
Визначення закону розподілу для генеральної сукупності
за вибірковими даними
|
Студент групи ПМ-12-1 |
|
Федіна С.А
|
|
Керівник канд. пед. наук, доцент |
|
Григорук С.С.
|
2014
Позначення та скорочення
ВМВ – велика механічна вибірка
ВГВ – велика групова вибірка
ВБВ – велика безповторна вибірка
ВПВ – велика повторна вибірка
ММВ – мала механічна вибірка
МГВ – мала групова вибірка
МБВ – мала безповторна вибірка
МПВ – мала повторна вибірка
ГС – генеральна сукупність
Зміст
Вступ 4
Розділ 1 Постановка задачі 4
Розділ 2 Теоретичні відомості 7
2.1 Генеральна та вибіркова сукупності 7
2.2 Впорядкування даних 9
2.3 Емпірична функція розподілу 10
2.4 Графічне зображення статистичних розподілів 11
2.5 Числові характеристики вибіркової сукупності 11
2.6 Абсолютна та відносна похибки 14
2.7 Закони розподілу 14
2.8 Статистичні гіпотези 15
2.9 Критерії узгодження 16
Розділ 3 Хід роботи 19
3.1 Підготовка даних до подальшої обробки 19
3.2 Графічне представлення інтервальних радів 20
3.3 Числові характеристики 21
Розділ 4 Висновок 27
Розділ 5 Додатки 28
5.1 Додаток А 28
5.2 Додаток С 33
5.3 Додаток D 38
5.4 Додаток Е 42
5.5 Додаток F 44
5.5 Додаток G 47
5.5 Додаток H 51
5.5 Додаток I 54
Вступ
Математична статистика – це наука, що створює нові та вивчає вже існуючі методи систематизації та використання статистичних даних для наукових та практичних висновків. Саме завдяки математичній статистиці працюють мільйони машин, вдачно запускаються космічні кораблі та багато ін.
Будь-яка подія або декілька подій зв’язаних між собою можуть вплинути на плин речей. Саме завдяки математичній статистиці можна отримати ймовірність настання даної події. Однак математична статистика – наука, яка влаштована дуже цікаво. Вміння її використовувати – мистецтво, що потребує не тільки знань, а й практики, наполегливості, досвіду та інтуіції.
Найвідомішими напрямами математичної статистики є описова статистика, теорія оцінювання і теорія перевірки гіпотез. Описова статистика – це сукупність емпіричних методів, що використовуються для візуалізації та інтерпретації даних (розрахунок вибіркових характеристик, таблиці, діаграми, графіки і т. п.).
Слід зазначити, що в наш час сучасні комп’ютери зробили можливими обчислення, які були раніше майже не можливі, або займали дуже багато часу. Також це викликало створення низки нових напрямів розвитку математичної статистики таких, як послідовний аналіз та загальна теорія статистичних рішень, які тісно пов'язані з теорією ігор. Іншим прикладом використання можливостей сучасних комп’ютерів є кластерний аналіз, націлений на виділення груп об'єктів, схожих один на одного, і багатовимірне шкалювання, що дозволяє наочно уявити об'єкти на площині.
До основних завдань математичної статистики можна віднести наступні великі класи задач:
– встановлення законів розподілу різних випадкових змінних, одержаних у результаті статистичного спостереження;
– перевірка статистичних гіпотез;
Розділ1 Постановка задачі
Початкові дані: Розглядається генеральна сукупність (500од., таблиця А.1), яка містить розподіл ознаки, котрий вивчається та відповідає одному з 5–ти наступних законів розподілу:
експоненціальний.
бетта–розподіл;
логарифмічно–нормальний;
рівномірний;
нормальний.
Зробити з генеральної сукупності 8 вибірок:
велику вибірку (200 од.) методом випадкового безповторного відбору;
велику вибірку (200 од.) методом випадкового повторного відбору;
велику вибірку (200 од.) методом механічного відбору (вибирається кожна 2–а одиниця);
велику вибірку (200 од.) методом групового відбору, починаючи з № варіанта + 200;
малу вибірку (25 од.) методом групового відбору, починаючи з № варіанта;
малу вибірку (25 од.) методом випадкового безповторного відбору;
малу вибірку (25 од.) методом випадкового повторного відбору;
малу вибірку методом механічного відбору (вибирається кожна 20–а одиниця);
Для кожної вибірки побудувати інтервальний варіаційний ряд і емпіричну функцію розподілу. Для малих вибірок число інтервалів прийняти рівним 5, для великих – 15.
Кожен інтервальний ряд представити графічно, у вигляді гістограми частот, полігону частот (сполучаючи середини стовпців гістограми частот), гістограми накопичених частот, а також графіку функції розподілу. За формою гістограми, полігону і графіку зробити припущення про можливий вид закону розподілу.
За допомогою вбудованої функції Microsoft Excel “Описова статистика” (команда меню «Сервіс» \ «Аналіз даних») визначити для генеральної та вибіркових сукупностей наступні параметри:
середні вибіркові для вибірок і математичне очікування для генеральної сукупності;
дисперсію;
середнє квадратичне відхилення;
коефіцієнт варіації.
моду;
медіану;
асиметрію;
ексцес.
Проаналізувавши одержані дані, зробити висновок про ступінь однорідності вибірок. Зробити висновок про форму кривої розподілу на предмет зсуву вершини щодо центру розподілу і ступеня “крутизни” вершини. Порівняти вибіркові характеристики з генеральними та зробити висновок щодо точності методів відбору, обчисливши абсолютні та відносні похибки.
Згідно результатів аналізу, висунути гіпотезу про вид закону розподілу ознаки в досліджуваній генеральній сукупності по великих вибірках. Визначити оцінки параметрів розподілу методом моментів. Побу–дувати графіки для кожної одержаної моделі, наклавши їх на відповідні полігони.
Виконати перевірку правильності гіпотези, використо–вуючи критерій 2.
Якщо гіпотеза виявилася невірною, повторити п. 1.5. і 1.6, висуваючи нове припущення про вид розподілу (обмежитися запропонованими розподілами).
Зробити висновки.
Теоретичні відомості
Генеральна та вибіркова сукупності
Нехай необхідно вивчити деяку сукупність однорідних об’єктів відносно деякої якісної чи кількісної ознаки, котра характеризує ці об’єкти. Наприклад, ми маємо партію деталей. Тоді якісною ознакою може бути стандартність дета–лі, а кількісною – контрольований її розмір.
Вся сукупність елементів, яку треба дослідити, називається генеральною сукупністю. Поняття генеральної сукупності, в певному сенсі, є аналогічним поняттю випадкової величини (закону розподілу ймовірностей), бо повністю обумовлене певним комплексом умов [1, с.188–189].
Отже, вибірковою сукупністю (вибіркою) називають сукупність випад-ково відібраних об’єктів.
Генеральною сукупністю називають сукупність об’єктів, з підмножини яких виконується вибірка.
Об’ємом сукупності називають число об’єктів цієї сукупності. Зазвичай позначають так: n=<розмір>.
Генеральна сукупність може мати, як скінченний, так і нескінченний об’єм. Саме причина неможливості дослідження генеральної сукупності з нескінченною кількістю елементів може слугувати поштовхом для створення вибірок. Також проблема дослідження вибіркової сукупності може бути пов’язана з певними економічними або часовими обмеженнями.
Вибіркову сукупність можна розглядати, як деякий емпіричний аналог генеральної сукупності. Згідно вибірки можна робити висновки про властивості генеральної сукупністі.
Властивості вибірки:
об’ємність – чим більший об’єм вибірки у відсотковому відношенні, тим точніший результат;
представницькість та репрезентативність – вибірка повинна містити представників усіх типових груп генеральної сукупності із збереженням співвідношень.
Мала вибірка – це вибірка, яка містить менше 30 елементів. Для соціальних процесів – 60 елементів.
Велика вибірка – це вибірка, яка містить більше 30 елементів. Для соціальних процесів – більше 60 елементів.
Способи відбору:
В математичній статистиці використовуються різноманітні методи відбору [1, с.190–191]. Їх можна розділити на два типи:
Відбір, не потребуючий розділу генеральної сукупності на частини:
простий випадковий безповторний відбір;
простий випадковий повторний відбір.
Відбір, при якому генеральна сукупність розбивається на частини:
типовий відбір;
механічний відбір;
серійний відбір.
Випадковий спосіб відбору (випадковий відбір) – це такий спосіб формування вибіркової сукупності, коли відбір одиниць з генеральної сукупності здійснюється у випадковому порядку. Випадковість відбору полягає у дотриманні принципу однакової можливості для всіх одиниць генеральної сукупності потрапити у вибірку.
Випадкова вибірка може бути організована або за схемою повторного відбору, або за схемою безповторного відбору. Зазначені схеми відбору дають однакові результати лише у разі нескінченної генеральної сукупності. За умо-вою скінченності генеральної сукупності, результати вибірок будуть різні. Особливість названих схем відбору полягає у наступному:
при повторному відборі кожна одиниця бере участь у вибірці стільки разів, скільки відбирається одиниць, тобто після реєстрації вона повертається у генеральну сукупність і в подальшому може знов потрапити у вибіркову сукупність. За таких умов генеральна сукупність залишається незмінною, і тому для всіх одиниць сукупності забезпечується рівна ймовірність потрапити у вибірку.
При безповторному відборі кожна відібрана одиниця у подальшому відборі не бере участі, тобто не повертається у генеральну сукупність. Але це означає, що чисельність генеральної сукупності буде змінною після кожної операції відбору. У зв'язку з цим, ймовірність потрапити у вибірку решти одиниць підвищується, а тому середня помилка вибірки тут буде менша, ніж при повторному способі відбору.
Механічним називається відбір, при якому генеральна сукупність поділяється на рівні частини відповідно до природного розташування її одиниць (географічного, просторового, алфавітного тощо) і з кожної частини обстежується одна одиниця. Тобто одиниці відбирають через рівні проміжки у порядку розташування їх сукупності.
Механічний спосіб забезпечує рівномірність відбору одиниць з усіх частин сукупності, тобто їх пропорційне представництво, а отже, і найбільш високу репрезентативність обстеження.
Слід зазначити, що при механічному способі відбору відібрані одиниці не мають імовірнісного характеру. Випадкові помилки тут зумовлюються не способом відбору, а наявністю випадковості у розташуванні матеріалу дослід-жуваної сукупності.
Груповий відбір – це такий спосіб формування вибіркової сукупності, коли відбір одиниць з генеральної сукупності здійснюється у послідовному порядку від зазначеного елемента, і вибирається n–на кількість елементів.
Впорядкування даних
Статистичні ряди розподілу є одним з найважливіших елементів статистики. Однак першочергово необхідно провести зведення та групування матеріалів статистичного спостереження. Результати подаються у вигляді статистичних рядів розподілу.
Варіаційний (статистичний) ряд – таблиця, перша стрічка якої містить елементи в порядку зростання, а друга – частоту їх появи.
Ранжований ряд розподілу – це ряд, в якому значення розташовуються в зростаючому або спадаючому порядку.
Відносна частота – це відношення частоти інтервалу до об’єму вибірки.
Інтервальний ряд – це ряд, в якому значення варіанти задається у вигляді інтервалу. Він використовується для полегшення обробки статистичної інфор-мації на великих вибірках та у випадках, коли частоти варіант мало відріз-няються між собою, а варіанти розташовані близько одна до одної.
Кількість інтервалів для інтервального ряду обраховується за формулою Стреджерса:
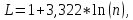 (2.2.1)
(2.2.1)
Частота – це числа, які показують, скільки разів повторюються окремі значення варіант.
Накопичена частота – сума частот чергового інтервалу, починаючи з першого і закінчуючи останнім.
Емпірична функція розподілу
Емпіричною функцією розподілу F*(x) називається відносна частота того, що ознака (випадкова величина) Х прийме значення, менше заданого аргументу х [3, с.8–13].
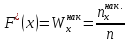 , (2.3.1)
, (2.3.1)
Властивості F*(x):
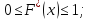
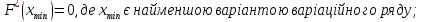
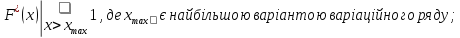
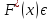 неспадною функцією
аргументу х, тобто
неспадною функцією
аргументу х, тобто

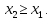
Графічне зображення статистичних розподілів
Полігоном частот називають ламану, відрізки якої сполучають точки (x 1,n 1), (x 2, n 2),..., (x k,n k). Для побудови полігону частот на осі абсцис відкладають варіанти х i, а на осі ординат – відповідні їм частоти n i.. Точки (x i, n i) з'єднують відрізками прямих і отримують полігон частот.
Гістограмою частот
називають ступінчасту фігуру, яка
складається з прямокутників, основами
яких є інтервали довжиною h, а висоти
дорівнюють
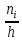 (щільність частоти). Площа гістограми
частот дорівнює об’єму вибірки
[4, с.12].
(щільність частоти). Площа гістограми
частот дорівнює об’єму вибірки
[4, с.12].
Зауваження 1 Гістограму можна побудувати тільки для інтервального статистичного розподілу.
Зауваження 2 Очевидно, що при збільшенні n можна вибрати все більш малі інтервали (h), при цьому гістограма буде наближатися до деякої кривої, яка обмежує площу близьку до 1. Ця крива є графіком щільності розподілу випадкової величини X.
Зауваження 3 Полігон і гістограма – аналогічні криві розподілу ознаки X, а емпірична функція розподілу F * (x) – функція розподілу випадкової вели–чини X.
Числові характеристики вибіркової сукупності
Числові характеристики варіаційних рядів – набір значень, які зображають деякі сталі величини,що подають варіаційний ряд в цілому і відображають властивості, сукупності закономірностей, що вивчаються. До таких числових характеристик відносяться середня величина ряду розподілу, величини, які відображають варіацію змін – розмах, дисперсія, середнє квад-ратичне відхилення та інші [4, c.34–42].
Математичне сподівання – це середнє арифметичне значень випадкової величини. Його знайдемо за формулою:
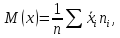 (2.5.1)
(2.5.1)
Дисперсія – це числова характеристика випадкової величини, яка вказує ступінь розсіювання цієї величини навколо її математичного сподівання. Дисперсія обчислюється за формулою:
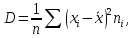 (2.5.2)
(2.5.2)
Середнє
квадратичне відхилення
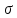 – індикатор мінливості об’єкта, що
показує на скільки в середньому
відхиляються індивідуальні значення
ознаки від їх середньої величини.
– індикатор мінливості об’єкта, що
показує на скільки в середньому
відхиляються індивідуальні значення
ознаки від їх середньої величини.
Середнє квадратичне обчислимо за формулою:
 , (2.5.3)
, (2.5.3)
Мода – найбільш ймовірне значення випадкової величини.
Випадкова величина, яка має лише одну моду, називається унімодальною.
Випадкова величина, яка має дві і більше моди, називається полі –модальною.
Моду обчислюємо за формулою [3, c.14]:
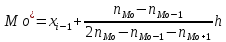 , (2.5.4)
, (2.5.4)
де
 –
початок модального інтервалу;
–
початок модального інтервалу;
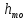 – довжина
модального інтервалу;
– довжина
модального інтервалу;
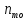 – частота
модального інтервалу
– частота
модального інтервалу
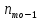 – частота
інтервалу, що передує модальному;
– частота
інтервалу, що передує модальному;
 – частота
інтервалу, що після модального.
– частота
інтервалу, що після модального.
Медіана – варіанта, що поділяє варіаційний ряд на дві рівні частини за кількістю варіант.
Медіана обчислюється за наступною формулою:
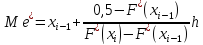 , (2.5.5)
, (2.5.5)
де
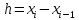 –довжина
інтервалу.
–довжина
інтервалу.
Коефіцієнт варіації – це характеристика однорідності вибірки. Визначається за формулою:
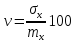 , (2.5.6)
, (2.5.6)
Асиметрія – це числова характеристика, яка визначає ступінь скошеності розподілу і обчислюється за формулою:
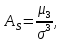 (2.5.7)
(2.5.7)
Якщо
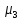 =0–
розподіл
симетричний.
=0–
розподіл
симетричний.
Якщо
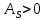 – правостороння асиметрія (
– правостороння асиметрія ( .
.
Якщо
 – лівостороння
асиметрія (
– лівостороння
асиметрія ( .
.
Ексцес – числова характеристика, яка характеризує «крутість» розподілу та обчислюється за формулою:
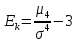 , (2.5.8)
, (2.5.8)
Ексцес, як
правило, використовується при дослідженні
неперервних ознак генеральних сукупностей,
оскільки він оцінює крутизну закону
розподілу випадкової величини порівняно
з нормальним. Для нормального закону
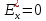 .
.
Абсолютна та відносна похибки
Абсолютна похибка – це абсолютна різниця (модуль різниці) між результатом вимірювання та умовно істинним значенням вимірювальної величини. Абсолютна похибка обчислюється за формулою:
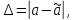 (2.6.1)
(2.6.1)
де а – істинне значення генеральної сукупності;
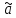 –значення числової
характеристики вибірки.
–значення числової
характеристики вибірки.
Відносна похибка – це відношення абсолютної похибки до істинного значення випадкової величини. Відносну похибку можна знайти за формулою:
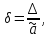 (2.6.2)
(2.6.2)
Закони розподілу
З вище зазначених законів розподілу найбільш відповідним до генеральної сукупності є нормальний розподіл.
Нормальний розподіл
Нормальний закон розподілу відіграє виключно важливу роль в теорії ймовірностей і займає серед інших законів розподілу особливий стан.
Це закон, який найчастіше зустрічається на практиці. Головна особливість, яка виділяє нормальний закон серед інших законів, полягає в тому, що він є граничним законом, до якого наближаються інші закони розподілу.
Нормальний розподіл
– розподіл ймовірностей випадкової
величини, що характеризуються
![]() де
де ![]() — математичне
сподівання,
— математичне
сподівання, ![]() — дисперсія
випадкової величини.
Параметр
— дисперсія
випадкової величини.
Параметр ![]() також
відомий, як стандартний
відхил.
Розподіл із μ =
0 та σ 2 =
1 називають стандартним
нормальним розподілом.
також
відомий, як стандартний
відхил.
Розподіл із μ =
0 та σ 2 =
1 називають стандартним
нормальним розподілом.
Статистичні гіпотези
Для практичного використання методів теорії вірогідності та математи-чної статистики знання закона розподілу є дуже важливим. Знаючи закон розподілу, можливо вирішувати безліч практичних завдань. Саме тому будь яка обробка результатів досліджень повинна починатись з відповіді на питання: котрий закон розподілу відповідає наявній вибірці.
Ця проблема, зазвичай, вирішується за допомогою створення гіпотез.
Статистична гіпотеза – це припущення, що висувається щодо особливостей розподілу ймовірностей випадкової величини, яке перевіряється за результатами спостережень над нею.
Перевірка будь–якої статистичної гіпотези виконується наступним чином:
по наявній вибірці підраховується статистичний критерій;
на основі принципу значущості встановлюється рівень значущості – най-більше значення вірогідності, котре несумісне з визнанням випадковості експериментально обчисленого значення статистики критерію [5, 202-203].
Перевіряєма
гіпотеза називається нульовою та
позначається як
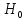 .
.
Конкуруючу
(альтернативну) гіпотезу
називають
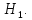
Існують як прості, так і складні гіпотези. Простою називають гіпотезу, яка містить всього одне припущення. Складною – яка складається зі скінчен-ного або нескінченного числа простих гіпотез.
Статистичним критерієм називають випадкову величину k, яка слугує для перевірки гіпотези.
Емпіричним критерієм називають те значення критерію, яке обчислено по вибірках.
Критичною областю називають сукупність значень критерію, при яких нульову гіпотезу приймають.
Областю прийняття гіпотези називають сукупність значень критерію, при яких нульову гіпотезу приймають.
Правосторонньою
називають критичну область, яка
визначається нерів-ністю
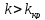 ,
де
,
де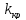 –
додатнє число.
–
додатнє число.
Лівосторонньою
називають критичну область, яка
визначається нерів-ністю
 ,
де
,
де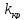 –
від’ємне число.
–
від’ємне число.
Критерії узгодження
Критерій узгодження
Пірсона (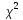 )
)
Критерій ґрунтується на порівнянні емпіричної гістограми розподілу випадкової величини з її теоретичною густиною. Діапазон зміни експери-ментальних даних розбивається на k інтервалів, та розраховується статистика [5, c.204–209]:
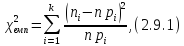
де
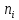 – кількість значень випадкової величини,
що входять в
i-тий
інтервал;
– кількість значень випадкової величини,
що входять в
i-тий
інтервал;
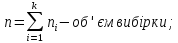
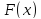 –гіпотетичний
теоретичний закон розподілу випадкової
величини;
–гіпотетичний
теоретичний закон розподілу випадкової
величини;
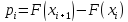 –теоретична
вірогідність
потрапляння випадкової величини в і-тий
інтервал.
–теоретична
вірогідність
потрапляння випадкової величини в і-тий
інтервал.
Для
знаходження
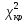 необхідно знайти ступінь свободи за
формулою:
необхідно знайти ступінь свободи за
формулою:
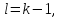 (2.9.2)
(2.9.2)
За [6]
знаходимо значення
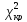 при
при
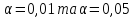 .За
умови,
якщо
.За
умови,
якщо
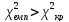 ,
то H0
відхиляється
з достовірністю (
,
то H0
відхиляється
з достовірністю (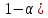 .
.
Критерій Колмогорова – Смірнова
У статистиці критерій узгодження Колмогорова (також відомий, як критерій згоди Колмогорова - Смірнова) [5, c. 214-216] використовується для того, щоб визначити, чи підпорядковуються два емпіричних розподіли одному закону, або визначити, чи підпорядковується отриманий розподіл передбачу-ваній моделі.
Критерій Колмогорова - Смірнова про перевірку гіпотези на однорід-ність двох емпіричних законів розподілу є одним з основних і найбільш широко використовуваних непараметричних методів тому, що досить чутливий до від-мінностей у досліджуваних вибірках.
Цей критерій також дозволяє оцінити суттєвість відмінностей між двома вибірками, у тому числі можливе його застосування для порівняння емпіричного розподілу з теоретичним.
Алгоритм критерію
записуємо інтервальний ряд
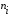 ≥
5;
≥
5;знаходимо середини інтервалів за формулою (2.9.2);
записуємо щільність розподілу f(x,c);
знаходимо параметри c;
записуємо F(x), f(x);
знаходимо
 ,
(2.9.3)
,
(2.9.3)
Шукаємо
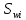 .
.Шукаємо різницю між накопиченими частотами відповідного порядку
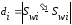 , (2.9.4)
, (2.9.4)
Знаходимо
 ;
;За таблицями критерію знаходимо
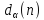 ;
;Якщо
 <
<
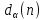 H0
приймається.
H0
приймається.
