Критерій Сільвестра.

Попередня теорема непридатна для практичного застосування, бо потрібно перевірити всі можливі значення змінних. а це не завжди легко.

Тому виникає потреба сформулювати таку теорему, яка дала б можливість легко визначити, чи форма f додатно означена. Така теорема є. Її називають критерієм Сільвестра.

Нехай задано дійсну квадратичну форму.

Випишемо матрицю квадратичної форми f:

Мінори

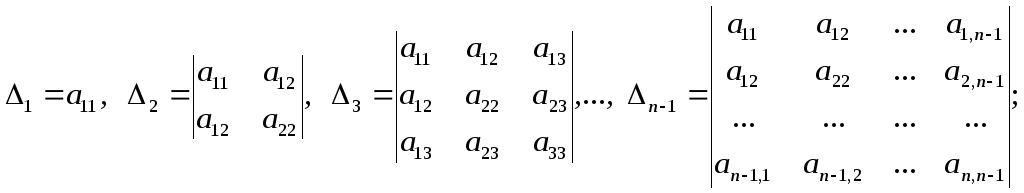
називається головними мінорами матриці А.

Теорема 2. (Критерій Сільвестра)

Дійсна квадратична форма буде додатно визначеною тоді і тільки тоді, коли всі її головні мінори строго додатні:

f – додатна означає

(Довести самостійно) Курош, §26 (ст. 159-161) – 3 сторінки.

Приклади.

При якому значенні квадратична форма буде додатно визначеною:

1)

.

Відповідь: .

2)

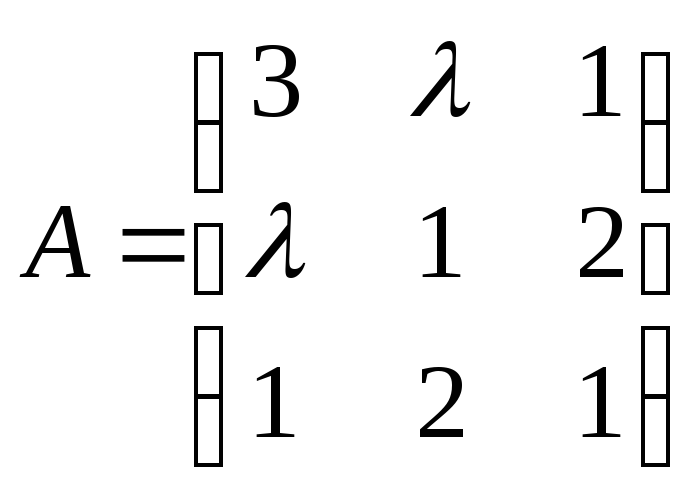
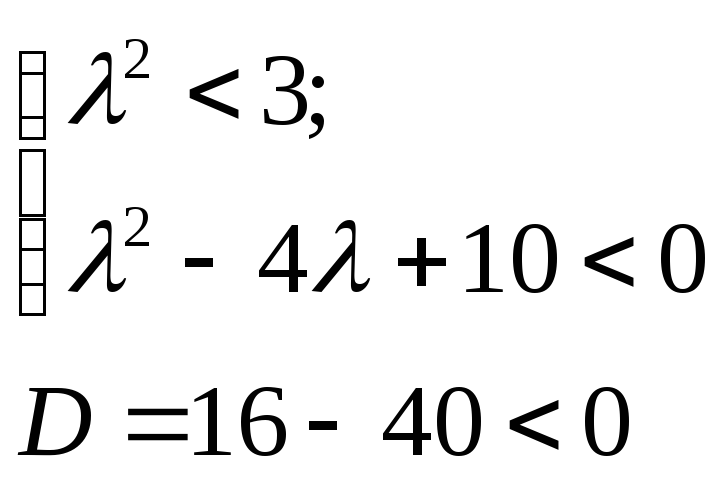
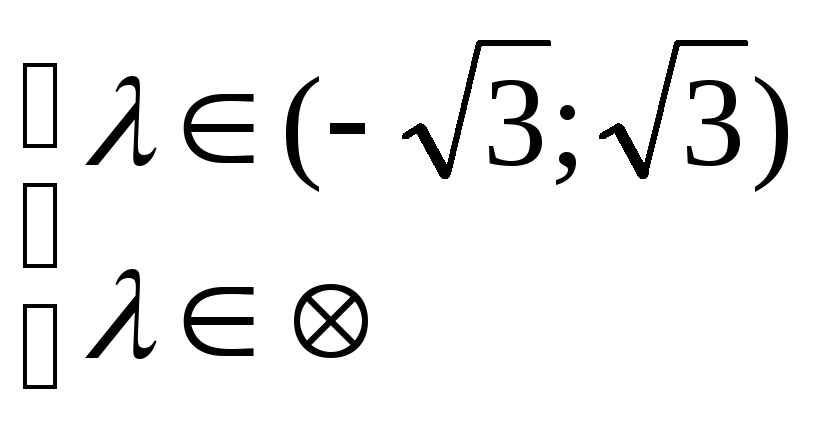
Відповідь: .

Квадратичні форми, що розкладаються на добуток лінійних форм.

Критерій розкладу

Розглянемо дві лінійні форми

Добуток двох лінійних форм завжди є квадратичною формою.

Виникає питання: чи кожна квадратична форма розкладається на добуток лінійних форм. Якщо ні, то коли це можливо.

Теорема 3: (критерій розкладу)

1) Комплексна квадратична форма розкладається на добуток лінійних форм т.і.т.т., коли її ранг.

2) Дійсна квадратична форма розкладається на добуток лінійних форм т.і.т.т., коли її ранг не перевищує 1, абоа сигнатура = 0.

Доведення І) 1) Нехай f – комплексна квадратична форма.

а)

б) лінійним невиродженим перетвореннямквадратична формаf зводиться до норм вигляду

в)

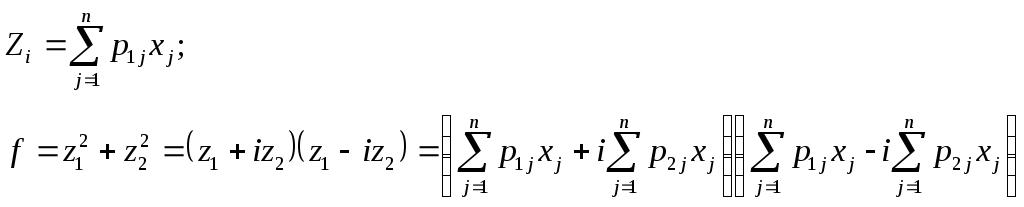
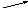
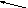
лінійні форми

2) Нехай – дійсна квадратична форма.

а)

б)

в)

ІІ) Обернене твердження.

1) Нехай .

а) якщо одна з цих форм нульова, то

б) якщо форми пропорційні.

Тоді

Виконаємо заміну в

в) Нехай і– не пропорційні. Це означає, що

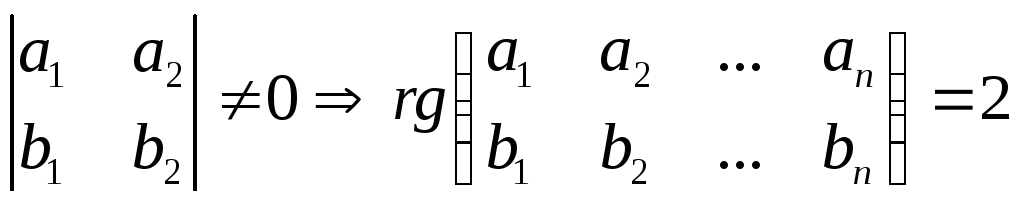
тоді лінійне не вироджене перетворення

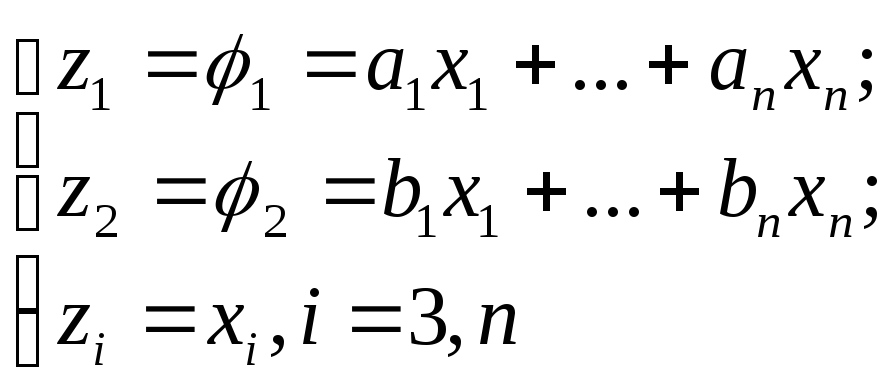
Форму f переводить у форму

Це квадратична форма має ранг = 2.

Якщо вона дійсна, то її сигнатура = 0:

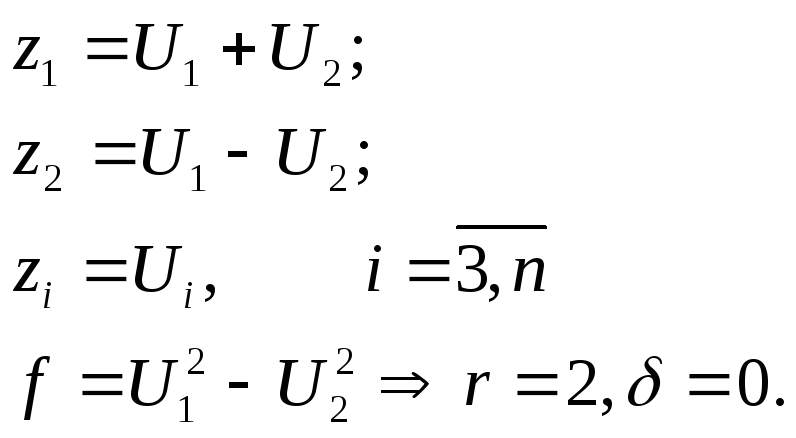
Теорему доведено.

Приклад: Розкласти на добуток лінійних форм квадратичну форму розклали

26