Закон інерції для дійсних квадратичних форм.

Нормальний вигляд квадратичної форми.

Означення 1. Квадратична форма називається називається нормальноюнормальною (або нормального вигляду квадратичної форми), якщо вона містить тільки квадрати змінних з коефіцієнтами, рівними 1 чи 0.

Іншими словами, нормальний вигляд квадратичної форми – це такий її канонічний вигляд, усі коефіцієнти біля квадратів = 1, 0.

Згідно з теоремою Лагранжа, існує лінійне не вироджене перетворення, яке квадратичну форму зводить до канонічного вигляду.

Оскільки при виконанні лінійного невиродженого перетворення ранг r квадратичної форми не змінюється, то

(1)

Розглянемо випадки, які найчастіше зустрічаються у застосуваннях квадратичної форми.

а) Нехай – комплексна квадратична форма, тобто₵

Виконаємо заміну:

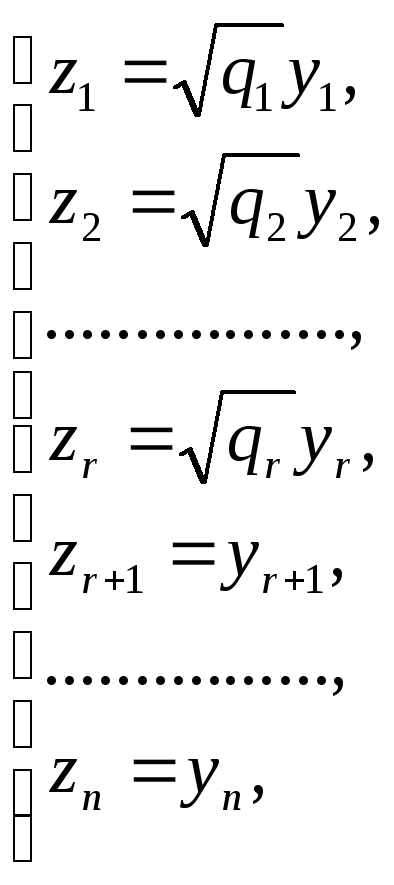(2)

Тоді

(3)

– нормальний вигляд квадратичної форми (всі коефіцієнти = 1)

б) Нехай f – дійсна квадратична форма, тоді

припустимо, що , а

при

Виконаємо заміну:

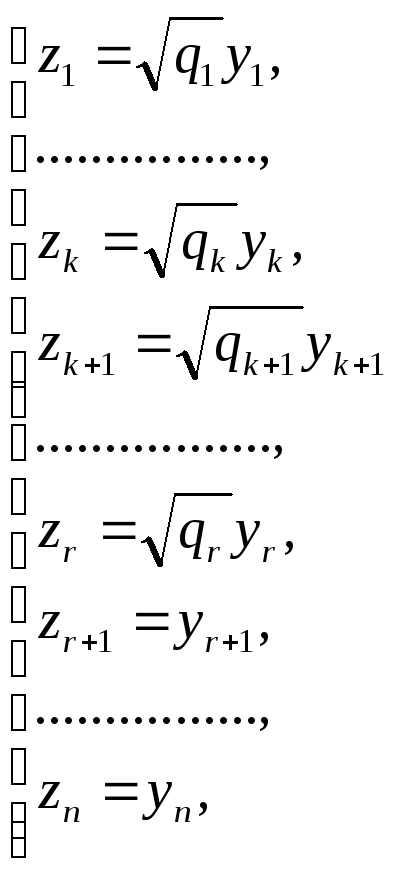(4)

Тоді

– нормальний вигляд дійсної квадратичної форми.

Мають місце твердження (доведені вище).

Твердження 1. Довільна комплексна квадратична форма лінійним не виродженим перетворенням змінних зводить до нормального вигляду, коефіцієнти в якому (біля ненульових квадратів) = «+1»

Твердження 2. дійсна квадратична форма лінійним не виродженим перетворенням зводить до нормального вигляду, у якому ненульові коефіцієнти = «+1».

Приклад. Розглянемо квадратичну форму.

На попередній лекції ми її звели до канонічного вигляду:

–над

Виконаємо заміну:

–нормальний вигляд квадратичної форми над

Закон інерції квадратичної форми

Теорема 3. (закон інерції квадратичної форми)

Кількість додатних квадратів у нормальному вигляді дійсної квадратичної форми не залежить від вибору дійсного лінійного не виродженого перетворення, за допомогою якого ці квадратична форма зводиться до нормального вигляду.

Доведеняя. Припустимо, що маємо дійсну квадратичну форму рангу.

Нехай ця квадратична форма лінійним не виродженим перетворенням

(6)

Зводиться до нормального вигляду

(7)

Припустимо, що перетворенням (лінійним невиродженим) вона

(8)

зводиться до вигляду:

(9)

Потрібно довести, що k=l . Доведення –від супротивного. Припустимо, що k<l .

Розглянемо систему рівнянь:

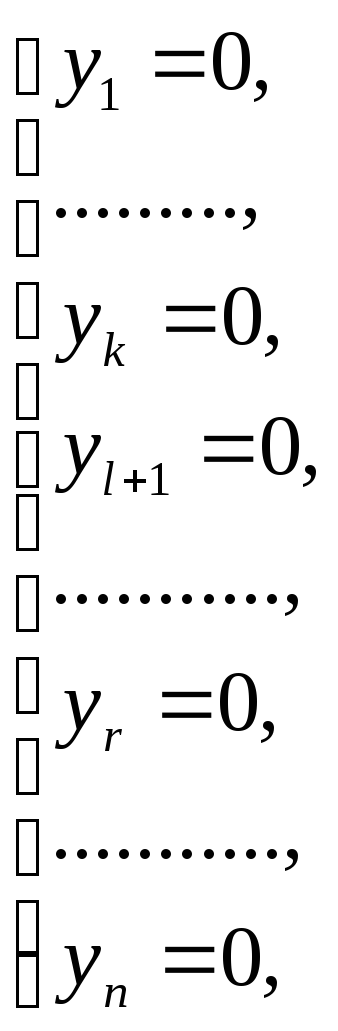(10)

Ця система містить рівнянь таn змінних (в силу (6),(8))

Оскільки систему (10) детальніше, враховуючи (6) та (8):

Це однорідне СЛР, у яких кількість менша кількості змінних вона є неозначеною (міститьрозв’язків).

Нехай – деякий нетривіальний розв’язок системи (10) (чи).

Враховуючи (6) і (8), отримаємо:

підставимо в (7) і (9).

Маємо:

(11)

Ця рівність можлива т. і т. т., коли :

(12)

Отже, враховуючи (10) і (12), отримаємо:

Звідси маємо, що система рівнянь:

,

яка містить n рівнянь і n змінних, має ненульовий розв’язок

Це можливо лише тоді, коли визначник системи .

А це означає, що перетворення (8) вироджене, що суперечить його вибору.

Отже, припущення k<l невірне.

Аналогічно доводиться, що припущення k>l є невірним.

Отже, k=l. Теорему доведено.

Означення 2. Кількість квадратів з додатними коефіцієнтами у нормальному вигляді дійсної квадратичної форми називається додатним індексом інерції квадратичної форми.

Кількість квадратів з від’ємними коефіцієнтами – від’ємним індексом інерції.

Позначення: та – відповідно.

Різницею -=називаютьсигнатурою квадратичної форми.

Співвідношення:

Нехай , тоді

(n – кількість змінних)

Приклад:

Нормальний вигляд: