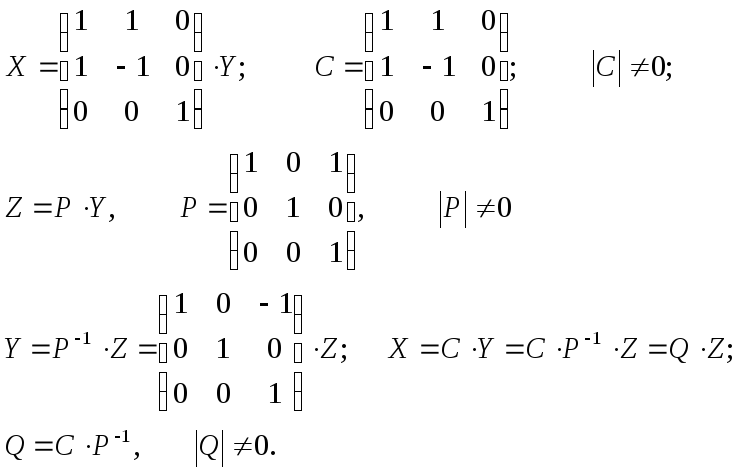Канонічний вигляд квадратичної форми. Теорема Лагранжа

Розглянемо наступну задачу:

Потрібно знайти таке лінійне не вироджене перетворення змінних, щоб отримана квадратична форма містила тільки квадрати змінних і не містить членів з добутками змінних.

Означення 4. Квадратична форма називаєтьсяканонічною (або канонічним виглядом квадратичної форми), якщо вона містить тільки суму квадратів змінних:

(7)

Нехай задана квадратична форма (1):

Припустимо, що знайдено таке перетворення

,

що

(8)

тобто отримали канонічний вигляд форми (1).

Нехай 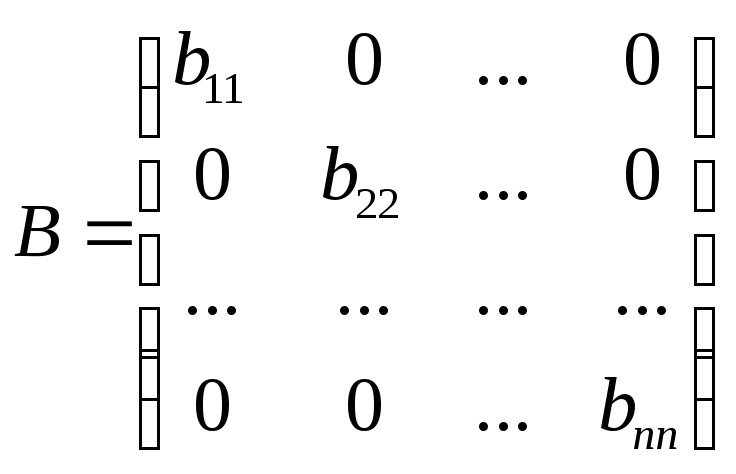– матриця канонічного вигляду.

І нехай

Оскільки, , а ранг матриціВ дорівнює кількості ненульових чисел , тоді отримаємо:

Висновок:

Якщо , то канонічний вигляд квадратичної форми f з матрицею А містить рівно r квадратів.

Виникає питання: чи кожну квадратичну форму можна звести до канонічного вигляду за допомогою лінійного не виродженого перетворення змінних?

Відповідь на це питання дає теорема!

Теорема Лагранжа (основна теорема про квадратичну форму):

Для довільної квадратичної форми існує лінійне не вироджене перетворення змінних, яке зводить її до канонічного вигляду.

Для будь-якої дійсної квадратичної форми існує лінійне не вироджене перетворення змінних, яке зводить її до канонічного вигляду.

Іншими словами: Кожна квадратична форма над полем Р може бути зведена деяким не виродженим лінійним перетворенням з коефіцієнтами їз Р до канонічного вигляду.

Доведення. Теорема доводиться методом математичної індукції за кількістю змінних.

Якщо n=1, то квадратична форма має вигляд, тобто теорема є вірною.

Нехай задано квадратичну форму:

, (1)

Розглянемо 2 випадки:

а) Нехай квадратична форма (1) має хоча б один квадрат змінної, тобто хоч один коефіцієнт при квадраті .

Наприклад .

1. Нехай 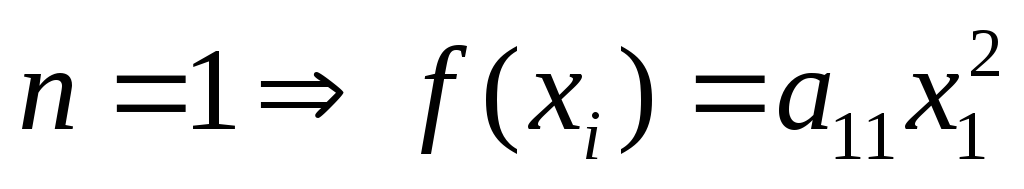–канонічний вигляд.

2. Нехай теорема вірна для квадратичної форми, які залежать від (п-1) змінних.

Розглянемо квадратичну форму:

і записуємо різницю.

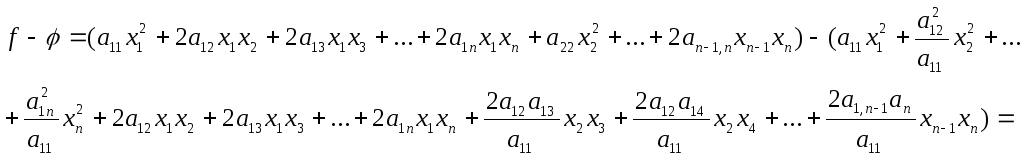
={всі доданки, що містять – зникають} =

Отже,

Введемо позначення:

(9)

Отримали лінійне перетворення змінних з матрицею:

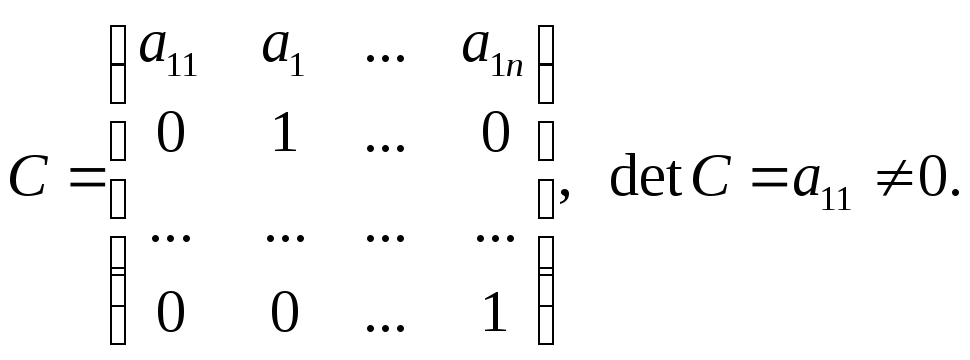
Отже, отримали лінійне перетворення –не вироджене: .

Квадратична форма прийме вигляд:

(10)

Квадратична форма залежить від (п-1) змінної. За припущенням, для таких форм теорема вірна. Тому існує лінійне квадратичне не вироджене перетворення змінних:

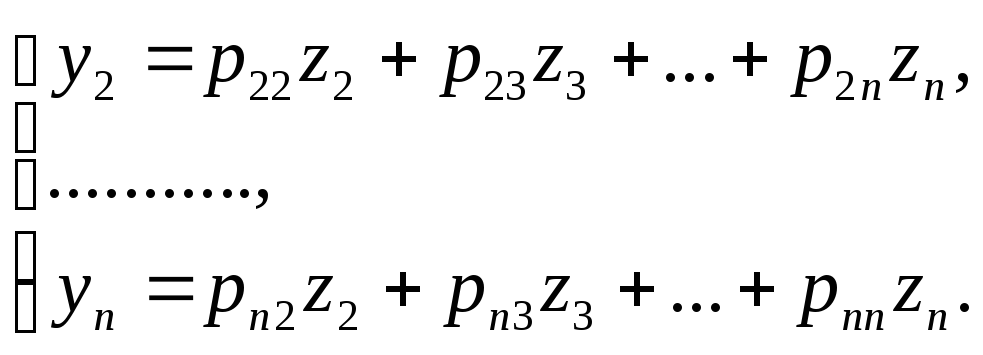(11)

де

Це перетворення зводить квадратичну форму до канонічного вигляду:

(12)

Тоді перетворення:

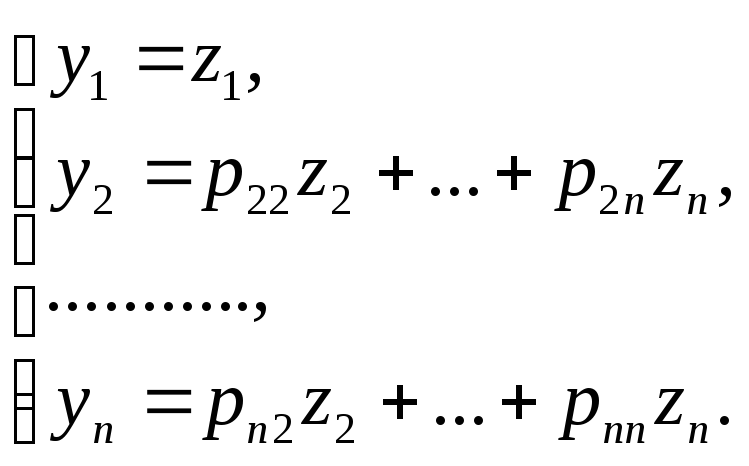(13)

є невиродженим, бо матриця:

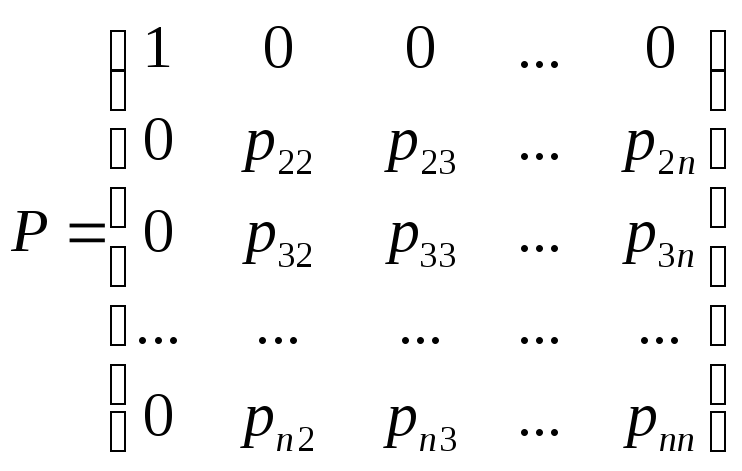є невиродженою

Лінійне перетворення (13) можна записати скорочено?

(13')

Отже, квадратична форма набуде вигляду:

(14)

Знайдемо фінальне перетворення:

яке приводить квадратичну форму f до канонічного вигляду (14).

Оскільки, із (9)

Оскільки, С та Р –не вироджені матриці, то матриця Q є не виродженою.

Тобто, теорему доведено для випадку

а).

б) Нехай у квадратичній формі (1) немає жодного квадрату:

У цьому випадку виконуємо заміну. Наприклад якщо , то

перетворення – не вироджене.

Після уього не виродженого перетворення квадратична форма (1) набуває вигляду:

і маємо квадрат однієї із змінних. Отже, таким перетворенням випадок б) зводиться до випадку а).

Тобто і в цьому випадку отримаємо, що квадратична форма зводиться до канонічного вигляду.

Теорему доведено.

Зауваження 1: Оскільки елементи матриць С і Р виражаються через коефіцієнти квадратичної форми, то вони будуть елементами того ж поля, що і квадратична форма (1).

Зауваження 2: Лінійне не вироджене перетворення , яке зводить квадратичну форму , до канонічного вигляду визначається неоднозначно.

Приклади:

1) – дійсна квадратична форма,.

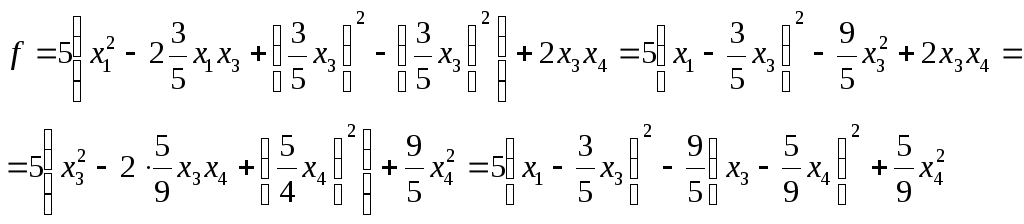
Виконаємо заміну:

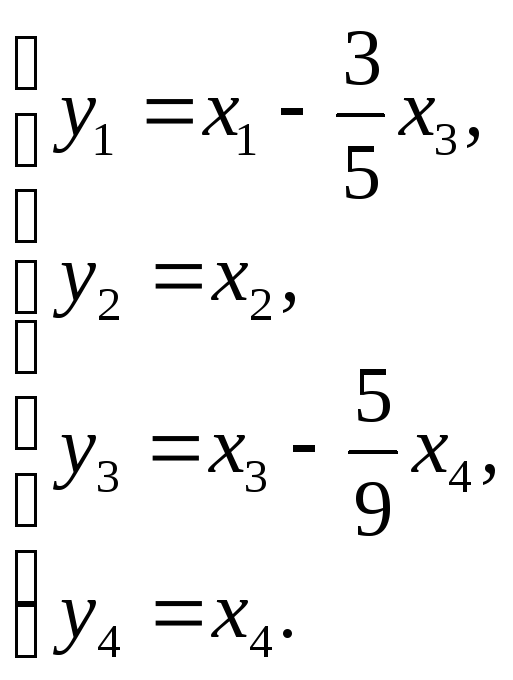
–канонічній вигляд квадратичної форми

квадратична форма вироджена.

Заміну змінних можна виконати по-іншому. Тому лінійне не вироджене перетворення визначається неоднозначно.

2)

Заміна:

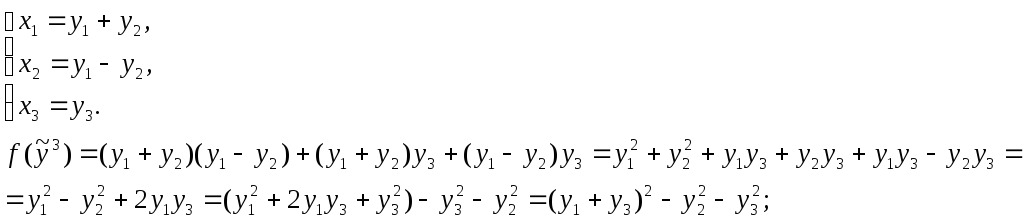
Заміна:

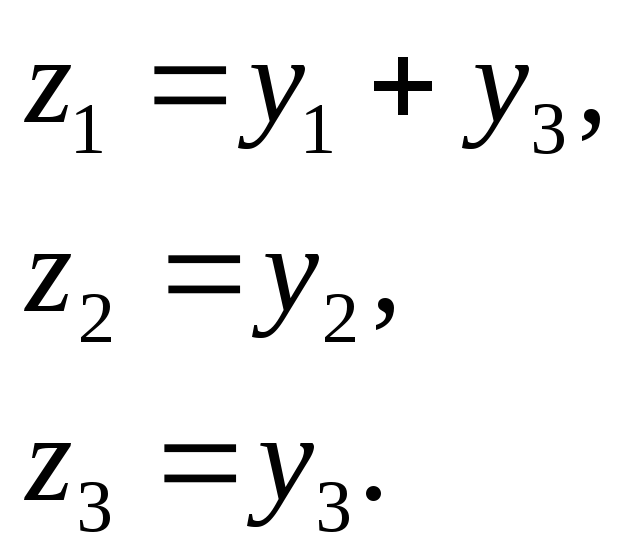
–квадратична невироджена форма.