Еквівалентність квадратичних форм.

Розглянемо ще одну задачу:

Нехай задано 2 квадратичні форми:

та

(від однакової кількості змінних). За якої умови існує лінійне не вироджене перетворення, яке перетворює одну квадратичну форму в іншу?

Означення 3. Дві квадратичні форми від n змінних називається еквівалентними, якщо одну з них можна перетворити до іншої за допомогою деякого лінійного перетворення змінних (для дійсних квадратичних форм це перетворення дійсне, для комплексних – комплексне).

Залишається тепер тільки сформулювати критерій (ознаку) еквівалентності двох квадратичних форм від n змінних.

а) Комплексні квадратичні форми.

Твердження 1. Дві комплексні квадратичної форми від n змінних еквівалентності тоді й тільки тоді, коли їх ранги рівні (однакові).

Доведення. Необхідність. Нехай квадратичні форми іеквівалентнііснує лінійне невироджене перетворення, яке приводить квадратичну формуf до квадратичної форми g.

Знайдемо лінійне перетворення, яке приводить f до нормального вигляду.

Оскільки f можні перевести в g, то нормальні вигляди в них будуть однакові. Тому:

.

Достатність. Нехай задано 2 комплексні квадратичні форми і.

Доведемо, що ̴

Якщо , толінійне невироджене перетворення

, яке квадратичну форму приводить до нормального вигляду:

Аналогічно, лінійне невироджене перетворення

, яке квадратичну форму приводить до нормального вигляду:

Отже, маємо:

;

Тоді можна записати, що:

Тобто лінійне невироджене перетворення

А це означає, що ̴.б) Дійсні квадратичні форми.

Твердження 5. Дві дійсні квадратичні форми від n змінних еквівалентні т.і т.т., коли їх ранги і сигнатури рівні.

̴

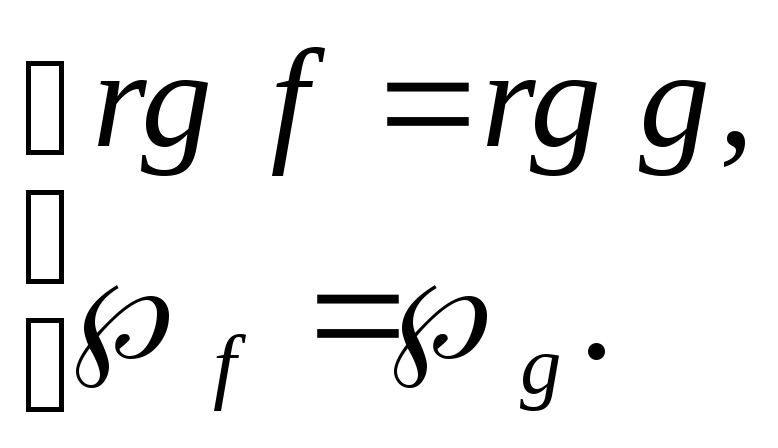
Самостійно.

Доведення. Достатність.

Нехай маємо дві дійсні квадратичні форми у яких

А це означає, що ці форми зводяться до одного і того ж нормальна вигляду:

Отже, лінійне невироджене перетворення, яке квадратичну формуf перетворює в g ̴(еквівалентні).

Необхідність. Нехай ̴. Тоділінійне невироджене перетворення, яке квадратичну формуf і g приводять до нормального вигляду.

Оскільки форми переводяться одна в одну, то нормальний вигляд в цих форм буде однаковий. Тому:

Класи еквівалентності квадратичної форми.

Означення 4. Кажуть, що дві квадратичні форми належать до одного класу еквівалентні, якщо вони еквівалентні.

Скільки різних класів еквівалентності є в дійсних квадратичних формах від n змінних?

Якщо , то класів еквівалентності є

Зокрема, якщо:

r=0, то класів є 1,

r=1, то класів є 2,

r=2, то класів є 3,

……………………,

r=n, то класів є n+1.

Всього маємо для квадратичної форми від n змінних:

класів еквівалентних форм.

Наприклад,

Розглянемо всі класи еквівалентності дійсної форми для n=3, n=4.

а) n=3:

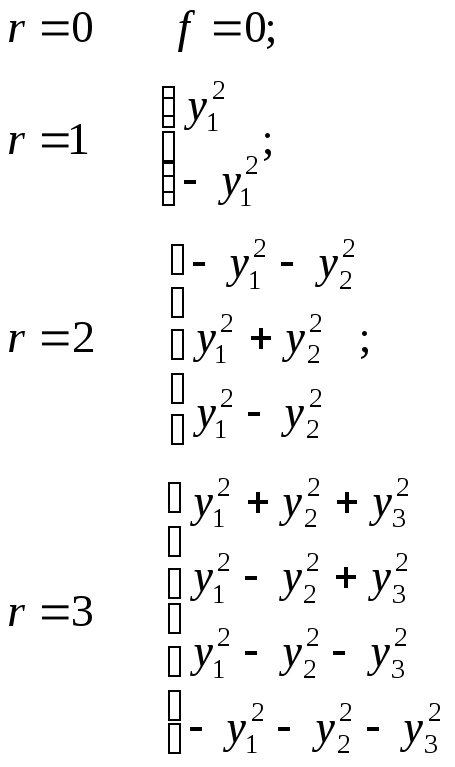
Всього 10 шт.

б) п=4

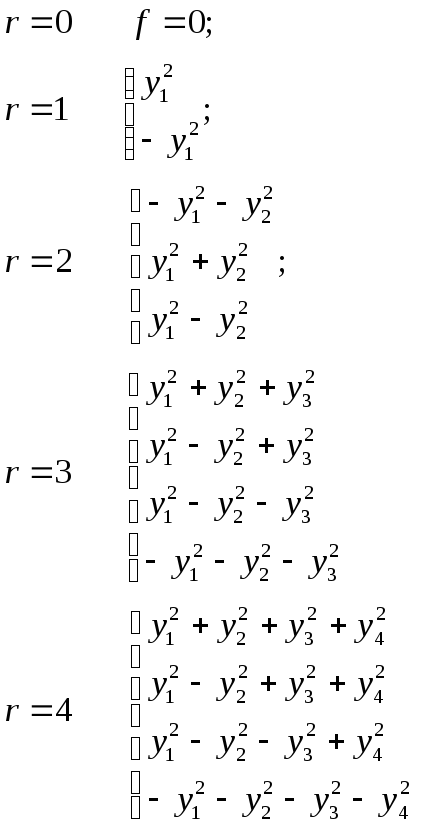
Всього 15 шт.

І так далі.

Додатно визначені квадратичні форми й ті, що розпадаються. Додатно визначені квадратичні форми.

Означення 1. Дійсна квадратична форма від n змінних називається додатно визначеною (означеною), якщо її нормальний вигляд містить n додатних квадратів:

–додатно визначені

Зауваження: Якщо то квадратичну формуf називають від’ємно визначеною.

Прикладом додатно визначеної квадратичної форми є формула квадрату віддалі між двома точками:

Позначимо:

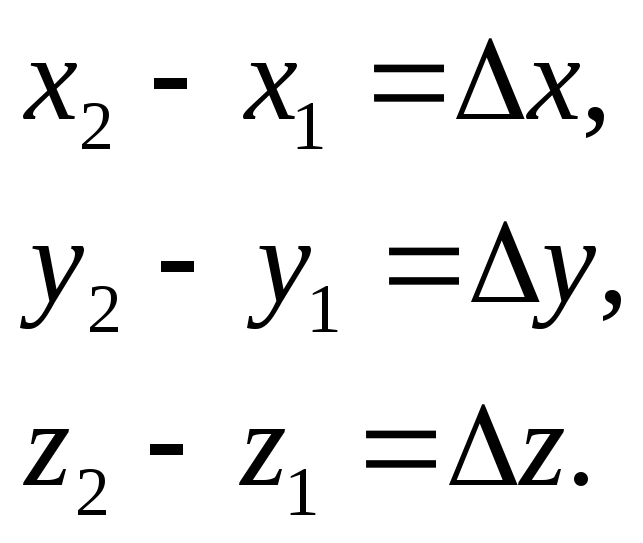
Теорема 1. (про числові значення додатно визначених квадратичних форм)

Дійсна квадратична форма від п змінних т.і т.т. буде додатно визначеною, коли при будь-яких ненульових значеннях змінних вона набуває додатного значення.

Або

Для того, щоб дійсна квадратична форма від п змінних була додатно визначеною, необхідно і досить, щоб всі її ненульові значення були додатними.

(без доведення).

Приклад 1. З’ясувати, чи квадратична форма f є додатно визначеною:

Розв’язання. Перепишемо цю квадратичну форму по-іншому:

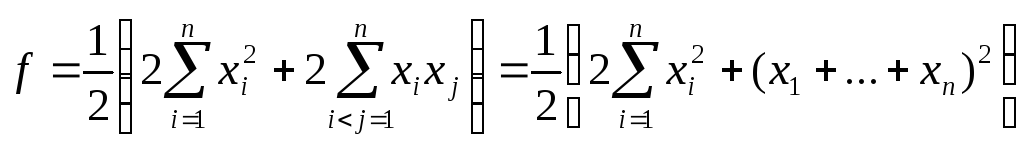
При довільних ненульових значеннях невідомих вона набуває додатних значеньf – додатно визначена.

Приклад 2.

–це очевидно виконується для всіх значень змінних.

З’ясуємо, чи може ця квадратична форма приймати нульові значення? Це, очевидно, може бути, коли:

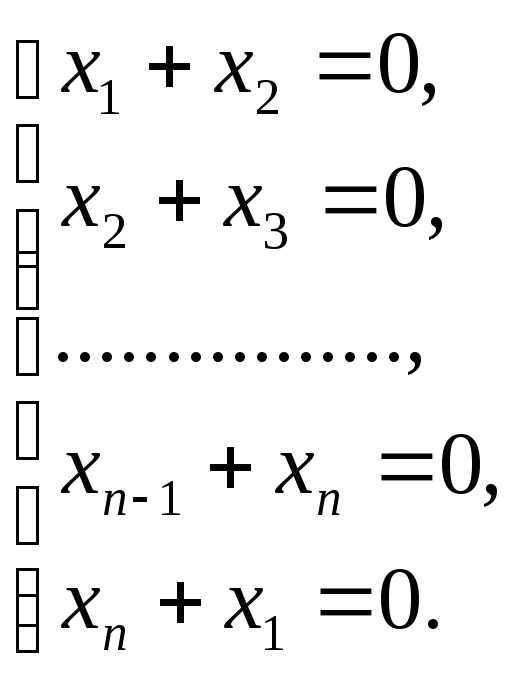
Розглянемо два випадки:

1) п – непарне. Запишемо знакозмінну суму:

при цих значеннях.

Отже, f не є додатно визначеною при парному п.

2) п- не парне. Приймемо

при цих значеннях. Отже, f не є додатньо визначеним при парному п.