Algebra_i_geometriya / ІІ модуль / NE_2.3 / приклади розв задач НЕ 2

Приклади розв’язування задач

Приклад 1. Знайти лінійне не вироджене перетворення, що зводить квадратичну форму до нормального вигляду:

а) .

Розв’язання.

Заміна: (2)

Матимемо: — нормальний вигляд даної квадратичної форми.

Знайдемо тепер перетворення, яке приводить квадратичну форму до нормального вигляду. Для цього виразимо через :

Із (2) маємо:

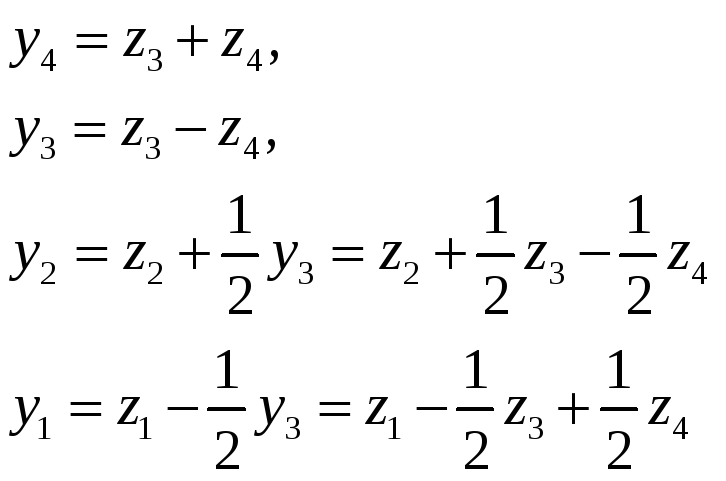
Підставимо ці вирази в (1):

Отже, шукане лінійне перетворення — таке:

— не вироджена перетворення не вироджене.

б)

Розв’язання.

Заміна:

— нормальний вигляд.

Перетворення:

Отже, шукане лінійне перетворення має вигляд:

Його матриця — не вироджена (бо ), тому знайдене перетворення не вироджене.

в)

Розв’язання.

Заміна:

Заміна:

— нормальний вигляд квадратичної форми

Перетворення:

— шукане перетворення.

Перетворення лінійне не вироджене, бо 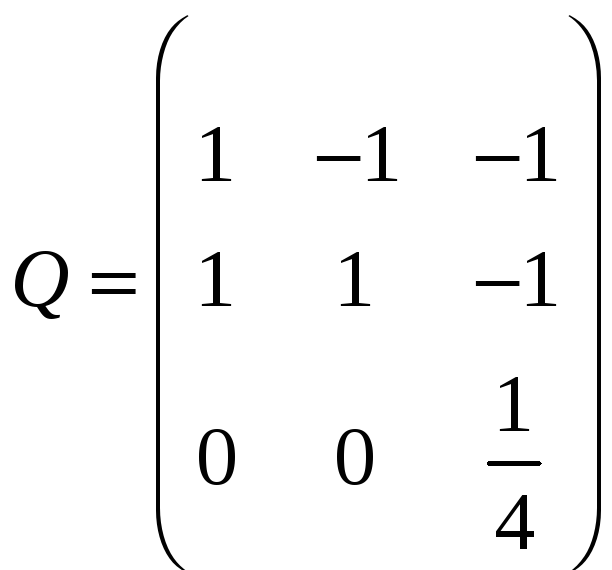— не вироджена ().

Приклад 2. Знайти всі значення параметра , при яких квадратична форма є додатно-визначеною.

Розв’язання.

Користуємося критерієм Сильвестра: Виписуємо матрицю квадратичної форми і обчислюємо її головні мінори:

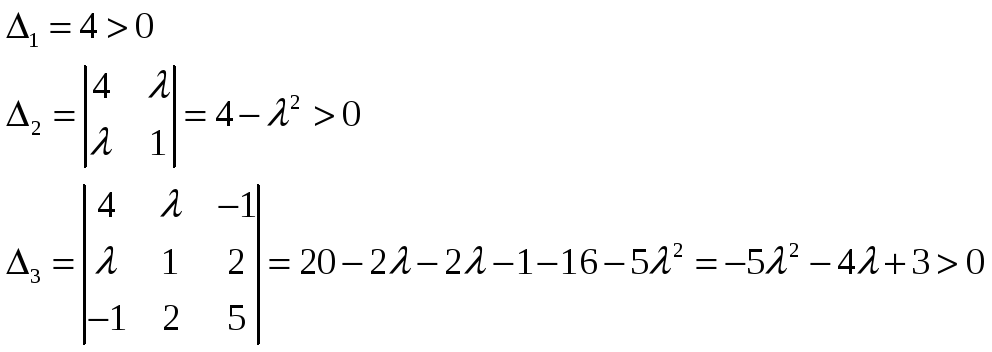
Отже, знаходимо із системи нерівностей:

Відповідь: При дана квадратична форма є додатно визначеною.

Приклад 3. З’ясувати, при якому значенні дійсна квадратична форма розпадається на добуток дійсних лінійних форм.

Розв’язання.

Згідно з критерієм, дійсна квадратична форма розпадається на добуток дійсних лінійних форм або та .

Отже, дослідимо спочатку ранг квадратичної форми, враховуючи, що , де

— матриця квадратичної форми

Оскільки у матриці А є ненульовий мінор , то .

Для того, щоб , тобто

Отже, при , тобто при таких значеннях квадратична форма є нерозпадною.

Якщо ж , то і квадратична форма розпадається на добуток лінійних форм, якщо ще й сигнатура . Тому шукаємо сигнатуру даної квадратичної форми. Для цього зводимо її до канонічного вигляду.

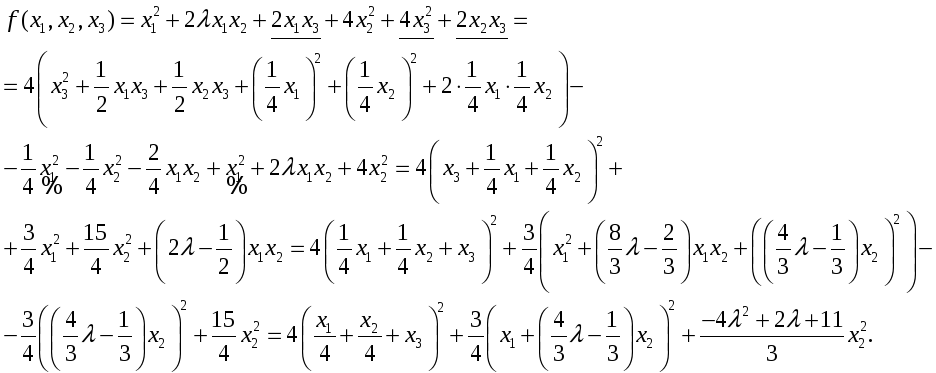
Заміна:

лінійне не вироджене перетворення, яке зводить квадратичну форму до канонічного вигляду:

Якщо , то , тому і вона має вигляд

, але

Отже квадратична форма ніколи не розпадається на добуток дійсних лінійних форм.

Приклад 4. Чи є еквівалентними квадратичні форми та

на полем дійсних чисел?

Розв’язання.

Квадратичні форми та будуть еквівалентними над , якщо

— ранги та сигнатури рівні.

Шукаємо ранги цих квадратичних форм за допомогою рангів їх матриць:

Отже, .

Отже

Залишається порівняти сигнатури. Для цього зводимо обидві квадратичні форми до нормального вигляду:

Заміна:

Тоді — нормальний вигляд квадратичної форми .

— сигнатура

Аналогічно,

Заміна:

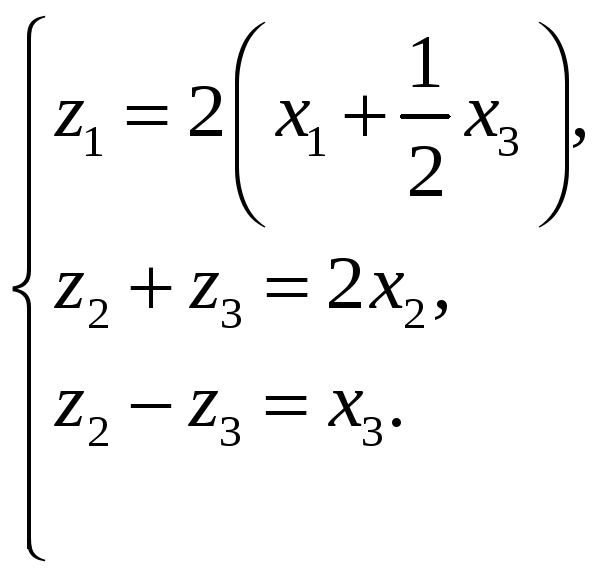
Тоді, — нормальний вигляд квадратичної форми .

—сигнатура .

Оскільки

То — вони еквівалентні.

6