Квадратичні форми. Їх канонічний вигляд.

Коли ми вивчали многочлени від багатьох змінних, то розглядали окремий їх випадок – симетричні множини.

Розглянемо ще один частковий випадок, коли всі одночлени мають однаковий степінь за сукупністю змінних, рівний 2.

Означення квадратичної форми.

Означення 1. Квадратичною формою f від п змінних над полем Р називається сума, кожен член якої є або добутком однієї із змінних, а коефіцієнти цих членів належать полю Р.

Якщо коефіцієнти є дійсними числами, то квадратичну форму називають дійсною; якщо є коефіцієнти є комплексними числами, то квадратичну форму називають комплексною.

Домовимося коефіцієнти при позначати через, а коефіцієнти добутку–через

Тоді при буде коефіцієнт –.

Оскільки , то можна записати:

Тобто вважаємо, що коефіцієнти і тому добуткупривідповідає коефіцієнт.

Отже, тепер квадратичну форму від п змінних можна записати у вигляді:

або скорочено

(1)

Із коефіцієнтів квадратичної форми побудуємо матрицю

(2)

А – матриця п­-го порядку, її називають матрицею квадратичної форми (1).

Оскільки , то матриця А – симетрична.

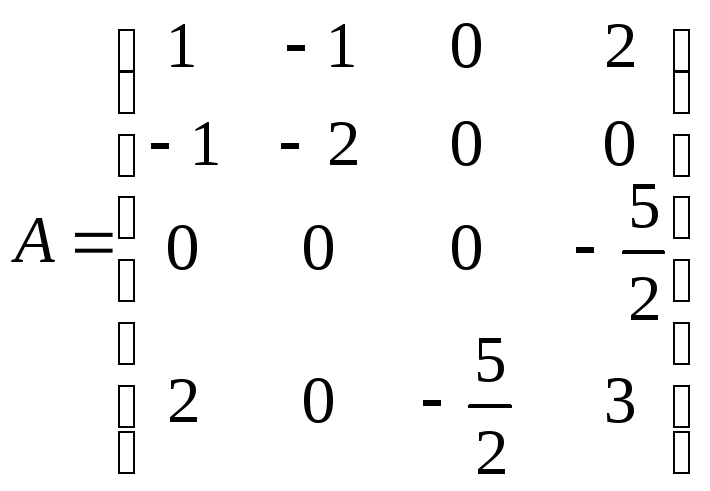
Наприклад:

Означення 2. Рангом квадратичної матриці форми f називають ранг матриці цієї форми:

Якщо , то квадратичну формуf називають не виродженою.

Якщо , то квадратичну формуf називають виродженою.

Приклади:

1) Розглянемо попередній приклад:

квадратична форма не вироджена

2)

квадратична форма вироджена.

Матричний запис квадратичної форми

Введемо позначення:

;

–матриця квадратичної форми

Обчислимо добуток:

= {один елемент, який дорівнює квадратній формі від змінних

} = (3)

Запис (3) називають матричним записом квадратичної форми (1)

Пізніше переконаємося, що при вивчені окремих питань, які стосуються квадратичних форм, зручно користуватися саме цим записом квадратичної форми.

Лінійне перетворення змінних квадратичної форми.

Розглянемо лінійне перетворення змінних, яке виражає змінні через :

(4)

Розглянемо матрицю лінійного перетворення:

та позначимо

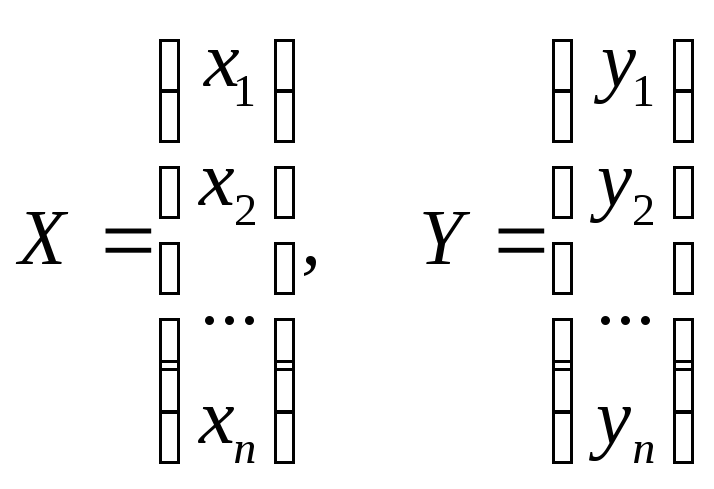
Тоді (4) можна записати скорочено:

(5)

Означення 3. Якщо , то лінійне перетворення змінних називаєтьсяне виродженим.

Має місце наступне твердження.

Лема 1. Матриця, транспонована до добутку матриць, дорівнює добутку транспонованих матриць, взятих у зворотному порядку:

(6)

Доведення.

Розглянемо:

тоді

причому

Обчислимо спочатку ліву частину рівності (6):

Для правої частини маємо:

З’ясуємо тепер, як змінюється матриця квадратичної форми, якщо над змінними виконати лінійне перетворення (4) з матрицею

Згідно з (3)

Отже, маємо:

де

Залишилось довести, що матриця В симетрична, тобто

Обчислимо

, (бо )

Висновок: При лінійному перетворені змінних з матрицею Q, квадратична форма з матрицею А переводиться в квадратичну форму з матрицею

Нехай лінійне перетворення буде не виродженим, тобто

Якщо , то внаслідок теореми про ранг матриць, можемо записати, що:

, якщо

Висновок: Лінійне не вироджене перетворення змінних не змінює рангу дійсної квадратичної форми.