
FTT-stud / view5
.pdfРОЗДІЛ 5. ЯВИЩА ПЕРЕНОСУ ВІЛЬНИХ НОСІЇВ ЗАРЯДУ У КРИСТАЛАХ
5.1. Теплоємність електронної системи металів і напівпровідників
Електронний газ у кристалі в першому наближенні розглядають як ансамбль майже вільних, не взаємодіючих між собою, подібно до молекул ідеального газу, квазічастинок – електронів, що знаходяться у постійному тепловому русі. Тому вони, як і фонони, повинні брати участь у процесах теплопередачі. Це означає, що теплоємність кристалу С можна подати у вигляді суми теплоємностей ґратки (системи атомних залишків, що коливаються
навколо |
положень рівноваги) Сгр |
і електронного |
газу(виродженого |
у металах і не |
|||
виродженого – у напівпровідниках) |
Сел. При цьому молярна теплоємність металів при |
||||||
високих |
температурах |
мала |
би |
становити |
якнайменше6R, а |
це |
суперечить |
експериментально встановленим закономірностям – законам Дюлонга-Пті і “Т 3”. |
|
||||||
Для вияснення причини малого впливу електронного газу у теплоємність металу необхідно згадати, що він є виродженим. Це означає, що при будь-якій температурі кристалу практично усі енергетичні стани аж до рівня Фермі заселені електронами. Отже, зазнавати термічного збудження (поглинати енергію при нагріванні кристалу, здійснюючи перехід на більш високий рівень) можуть тільки ті з них, які розміщені близько до рівня Фермі у інтервалі шириноюkBT. Оскільки при кімнатних температурах ця величина становить не більше 0,025 еВ, то змінювати енергію при нагріванні кристалу може лише невелика частка електронів.
Для оцінки цієї кількості, будемо вважати, що енергетичні рівні розподілені по зоні провідності рівномірно. Тоді можна стверджувати, що частка електронів, що зазнають термічного збудження при досягненні температури Т, становить величину kBT/μ, а кожний з них володіє енергією 3kBT/2. Якщо в зони провідності міститься N електронів, то енергія збудженої їх частини становить величину Еел = 3N(kBT)2/(2μ), а теплоємність електронного газу – Сел = 3NkB(kBТ/μ). Беручи до уваги, що при кімнатних температурах kBT/μ ≈ 0,005, а молярна теплоємність ґратки Сμ гр = 3R, знаходимо молярну теплоємність одновалентного металу Сμ = Сμ гр + Сμ ел = 1,005Сμ гр. ≈ Сμ гр.
Результатом більш строгої теорії теплоємності електронного газу є вираз |
|
|||||||
|
|
p 2 |
k BT |
|
|
|
||
Cел |
= |
|
|
Nk B ( |
|
) , |
(5.1) |
|
|
2 |
m |
||||||
|
|
|
|
|
|
|
||
що при кімнатній температурі також дає |
Сμ = 1,01Сμ |
гр. ≈ Сμ гр. Отже, в обох випадках |
||||||
одержується однаковий результат– |
теплоємність |
|
електронного газу не |
перевищує |
||||
відсотка від величини теплоємності ґратки металу. Причиною цього є надзвичайно мала кількість електронів виродженої системи, що можуть брати участь у тепловому русі.
Зауважимо також, що |
в області |
низьких |
температур |
теплоємність електронної |
системи змінюється лінійно, а ґратки – пропорційно до Т 3. Тому при T < TD теплоємність |
||||
електронного газу більша ґраткової. |
|
|
|
|
У напівпровідниках |
вільні носії |
заряду |
утворюють |
невироджений. Протегаз |
внаслідок малих концентрацій у напівпровідниках n- або p-типу, їх внесок у теплоємність кристалу також незначна. Така ситуація зберігається до появи властивої провідності напівпровідника, коли концентрація електронів і дірок істотно зростає, що спричиняє зростання їх внеску у теплоємність кристалу. Особливо великим він є при температурах, близьких до температури плавлення, де електронна теплоємність становить істотну частину теплоємності кристалу.
5.2. Рух вільних носіїв заряду в зовнішньому електричному полі
Характеристики руху кожного електрона(швидкість, переміщення) у будь-який момент часу визначаються його взаємодією з атомами ґратки, що хаотично коливаються
біля |
положень |
рівноваги |
та |
дефектами, розміщення |
яких |
у |
ґратці |
зазвичай |
невпорядковане. |
Зазвичай процеси |
розсіювання спрощено |
уявляють |
як послідовність |
||||
випадкових зіткнень електрона з дефектами ґратки або фононами. В результаті цього він випадковим чином змінює свій імпульс (напрям і, можливо, швидкість руху) та, у випадку не пружного зіткнення, – енергію. Тому за відсутності зовнішніх сил електрони рухаються
хаотично, а середня швидкість їхнього поступального руху в будь-якому напрямку
дорівнює нулю.
r r
Зовнішнє електричне поле, діючи на електрон з силою F = -eE , прискорює ті з них,
r
що рухаються протилежно до напрямку E . Рух електронів, швидкість яких збігається за напрямком з вектором напруженості поля, а – уповільнюється. В результаті порушується симетричність розподілу електронів за компонентами вектора швидкості– з’являється
відмінна від нуля середня швидкість поступального руху в напрямку, протилежному до r
E . Такий рух, подібний до руху за течією, називають дрейфом. Середня швидкість такого
руху називається дрейфовою. |
|
|
|
Оскільки дрейф |
здійснюють |
заряджені частинки– електрони, |
то має місце |
спрямоване перенесення |
заряду– у |
кристалі протікає електричний |
струм. У випадку |
створення умов для появи властивої провідності напівпровідника, струм в ньому забезпечується дрейфом електронів і, у протилежному напрямку, – дірок.
Напрямленому рухові вільних носіїв заряду у кристалах перешкоджає розсіювання– після кожного акту зіткнення з розсіюючим центром він змінює напрямок і швидкість руху. Тому при вимкненні електричного поля дрейф носіїв припиняється, їх рух знову стає рівноважним – хаотичним. Відповідно, зникає й електричний струм.
Значення дрейфової швидкості можна знайти на основі класичних |
уявлень як |
||
середню швидкість рівноприскореного руху |
|
||
uдр = |
at |
, |
(5.2) |
|
|||
2 |
|
|
|
де a = eE/m* – прискорення квазічастинки в електричному полі; τ – середній час її вільного пробігу між двома послідовними актами розсіювання, його можна оцінити як відношення середньої довжини вільного пробігу до середньої швидкості теплового . рухуОтже, дрейфова швидкість
uдр = |
et |
E . |
(5.3) |
|
2m* |
||||
|
|
|
Як уже зазначалося, наведені міркування ґрунтуються на найпростішій моделі електронного газу (електрони – молекули ідеального газу) та механізмів його взаємодій з фононами або домішками(механічні зіткнення) та зовнішнім полем(прискорення кожного електрона під дією кулонівських сил). Адже, уявлення про індивідуальність електрона у кристалі уже є наближенням. Більш строго процеси взаємодії електронної системи з зовнішнім полем описуються так званимкінетичним рівнянням Больцмана, яке являє собою аналог відомого в електродинаміці рівняння неперервності
r |
¶r |
|
div j = - |
||
¶t |
||
|
||
|
r |
у фазовому просторі координат та імпульсів (тут j - густина струму, а ρ – заряду). Кінетичне рівняння описує зміни функції розподілу електронів за швидкостями під
впливом зовнішніх полів і процесів розсіювання. Як показує його аналіз, наявність зовнішнього електричного поля, паралельного до вісіOx, спричиняє зсув щільності розподілу електронів за компонентою вектора швидкостіυx в напрямку діючої сили(рис. 5.1). Величина зміщення і є дрейфовою швидкістю υдр.
Після вимкнення зовнішнього поля закон розподілу повертається до рівноважного внаслідок розсіювання електронів. Цей процес називається релаксацією і відбувається він з певною скінченою швидкістю, що залежить від того в якому кристалі, на якій кількості і
яких центрів розсіюються електрони. Внаслідок релаксації електронів їх дрейфова швидкість зменшується за експоненціальним законом

Рис. 5.1. Зсув закону розподілу електронів швидкостями у зовнішньому електричному полі
uдр (t) = uдр (0)e-t /t рел , |
(5.4) |
||||||||
де t – проміжок часу, що пройшов з |
|||||||||
моменту |
|
вимкнення |
поля, |
υдр(0) |
– |
||||
величина дрейфової швидкості у момент |
|||||||||
вимкнення, |
τрел |
– |
час |
релаксації, |
– |
||||
величина, |
що |
характеризує |
швидкість |
||||||
переходу системи у рівноважний стан (за |
|||||||||
час t = |
|
τрел |
|
|
дрейфова |
швидкість |
|||
зменшується у е раз). |
|
|
|
||||||
З розв’язку кінетичного рівняння |
|||||||||
Больцмана |
|
для |
електронної системи |
||||||
кристалу |
в |
зовнішньому електричному |
|||||||
полі випливає, що дрейфова швидкість |
|||||||||
визначається формулою |
|
|
|
||||||
|
|
uдр |
= |
et рел |
|
E , |
(5.5) |
||
|
|
|
m* |
||||||
|
|
|
|
|
|
|
|
||
подібною до (5.3). Порівняння цих двох формул свідчить, що час релаксації у кінетичній теорії і середній час вільного пробігу у найпростішій класичній теорії мають відіграють однакову роль.
Усе сказане вище стосовно вільних електронів у досконалому напівпровіднику узагальнюється і на випадок носіїв іншого типу в ньому – дірок, а також на випадок носіїв у кристалах з електронною або дірковою провідностями.
Також можна стверджувати, що величина дрейфової швидкості носіїв визначається
чинниками як внутрішніми(типом |
носія – електрон |
і дірка |
мають, здебільшого, різні |
|||||||
ефективні маси; типом кристалу – |
значення m* і τрел |
визначаються його параметрами; |
||||||||
типом центрів розсіювання – значення τрел |
різні при розсіюванні на фононах різних мод, |
|||||||||
дефектах різного роду), так і зовнішніми(напруженістю |
електричного |
поля |
та |
|||||||
температурою кристалу – вона визначає |
середню швидкість |
теплового руху, а |
отже, |
і |
||||||
значення τрел). |
|
|
|
|
|
|
|
|
|
|
5.3. Залежність рухливості носіїв від температури |
|
|
|
|||||||
Формулу (5.5) можна подати і у вигляді |
|
|
|
|
||||||
|
|
uдр = mE , |
|
|
(5.6) |
|||||
де |
|
|
|
|
|
|
|
|
|
|
|
uдр |
|
et рел |
|
|
(5.7) |
||||
m = |
|
|
= |
|
|
|
|
|||
E |
m* |
|
|
|||||||
|
|
|
|
|
|
|
||||
– не залежна від характеристик зовнішнього поля величина, яка називається рухливістю
2 -1 -1
носія заряду, вимірюється в одиницях м∙В ∙с і має зміст дрейфової швидкості, якої набуває носій у полі з напруженістю 1 В/м.
Як показують вимірювання, виконані в германії при кімнатних температурах, рухливість електронів μе = 0,39 м2∙В-1∙с-1. Середня швидкість теплового руху
u =  8k BT /(p me* )
8k BT /(p me* )
електронів у такому кристалі при Т = 300 K становить величину 2,25∙105 м/с , а дрейфова, при напруженості 1 В/м, – 0,39 м/с. Поклавши в (5.12) me* = 0,23m0, отримуємо величину часу релаксації електронів у цьому кристаліτрел ≈ 5∙10-13 с і оцінку середньої довжини вільного пробігу електрона l = 1,12∙10-7 м, що у сотні раз перевищує міжатомну відстань.

Рухливість носіїв визначається величиною часу їх релаксації, яка, взагалі кажучи, залежить від їх енергії. Тому ця величина повинна усереднюватись по системі носіїв, причому по-різному, залежно від ступеня її виродженості.
У процесах розсіювання виродженого електронного газу можуть брати участь тільки частинки з енергією, близькою до енергії Фермі, тому рухливість визначається часом релаксації саме таких електронів:
me = |
e |
× |
|
lF |
, |
(5.8) |
|
m* |
uF |
||||||
|
|
|
|
||||
|
e |
|
|
|
|
|
|
де lF і υF, відповідно, – довжина вільного пробігу і швидкість руху квазічастинок.
У випадку невиродженого газу ступінь заповнення зон вільними носіями мала, тому рух кожного з них можна вважати незалежним від руху інших. Тоді рухливість
визначається значеннями довжини вільного пробігу та |
швидкості, усередненими по |
||||||
усьому ансамблю квазічастинок: |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
m = |
× |
l |
|
. |
(5.9) |
||
m* |
|
|
|||||
|
|
u |
|
|
|||
При цьому в обох випадках довжина вільного пробігу і швидкість теплового руху |
|||||||
визначаються значенням температури |
кристалу. Отже, й |
рухливість є функцією |
|||||
температури. Встановити явний вигляд цієї функції в загальному випадку неможливо, оскільки відповідальними за розсіювання процеси, вплив яких різний при різних температурах. Можна проаналізувати крайні випадки низьких(T < TD) і високих (T > TD) температур.
В області низьких температур концентрація фононів надзвичайно , малатому найімовірнішою причиною розсіювання електрона у кристалі є їх взаємодія з дефектами ґратки. Найчастіше це – розсіювання електрона позитивно або негативно зарядженим іоном домішкового атома. Розсіювання полягає в тому, що, пролітаючи повз домішковий центр, електрон відхиляється від попереднього напрямку руху. Величина кута відхилення залежить від швидкості електрона і його відстані до центра розсіювання. Оскільки названі
величини – випадкові, то |
кут розсіювання, |
а |
відповідно, і довжина вільного пробігу |
|||||||
електрона – випадкові |
величини. |
Середнє |
|
|
значення |
останньої |
можна |
оцінити, |
||
використавши формулу, виведену Резерфордом для аналізу процесів розсіюванняα- |
||||||||||
частинок на ядрах атомів |
|
|
|
|
|
|
|
|
|
|
|
l ~ |
mu 4 |
e |
|
2 |
, |
|
|
(5.10) |
|
|
|
× ( |
|
) |
|
|
|
|||
|
|
Ze |
|
|
|
|||||
|
|
Ni |
|
|
|
|
|
|
||
де Ni – концентрація іонів, заряд яких становить Ze; m і υ – відповідно, маса і швидкість частинки; ε – діелектрична проникність матеріалу. Така оцінка дозволяє стверджувати, що середня довжина вільного пробігу електрона пропорційна до четвертого ступеня середньої швидкості теплового руху. Відповідно, рухливість електронів при низьких температурах пропорційна до третього ступеня цієї величини і не залежить від температури у випадку виродженого електронного газу(μ ~ υF3) та пропорційне доT3/2 – у випадку невиродженого.
Ефективність розсівання електронів нейтральними домішками значно менша, ніж іонізованими. Однак повністю нехтувати ним неможливо, собливо в області дуже низьких температур (T << Ts), коли більша кількість домішкових атомів нейтральна. Вказане розсіювання можливе внаслідок одного з двох процесів: прямого пружного зіткнення або обмінної взаємодії, яку грубо можна трактувати як обмін місцями вільного електрона і локалізованого на домішковому .рівніЧас релаксації розсіювання на нейтральних домішках виявляється незалежним ні від температури, ні від енергії електрона провідності, а визначається тільки ефективною масою носія, концентрацією та типом домішкових атомів.

В області високих температур концентрація фононів настільки , великащо переважаючим є розсіювання електрона на коливаннях ґратки. Як свідчать результати квантової теорії розсіювання, найефективніше воно відбувається внаслідок взаємодії електронів з акустичними фононами. При цьому довжина вільного пробігу електрона виявляється незалежною від його енергії, а визначається тільки концентрацією фононів– обернено пропорційна до неї. Оскільки при високих температурах остання пропорційна до
Т, то незалежно від ступеня вродженості електронного газу довжина вільного пробігу пропорційна до 1/T. Отже, при (T > TD) μ ~ 1/T для виродженого і μ ~ 1/T3/2 – для
невиродженого електронного газу.
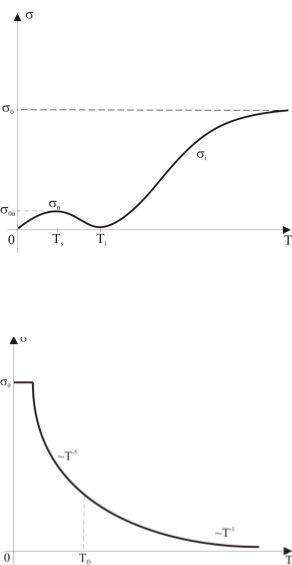
Для проміжних температур(T ≈ TD) суттєвими будуть процеси розсіювання як на домішках, так і на фононах, внесок яких по-різному впливає на рухливість. Результуюча дія цих процесів приведе до того, що залежність μ(Т) у невиродженому напівпровіднику буде характеризуватись наявністю максимуму, положення і висота якого визначається концентрацією домішки (рис. 5.2, а). Хід температурної залежності рухливості виродженого електронного газу схематично показаний на рис. 5.2, б.
а)
б)
Рис. 5.2. Температурна залежність рухливості електронів провіднос невиродженому (а) та виродженому (б) газі (крива 1 відповідає меншим, а 2 – більшим концентраціям домішки)
Спотворення кристалічної ґратки, викликані дислокаціями, спричиняють появу неоднорідності електричного поля, створеного її атомами. Це також може бути причиною розсіювання вільних носіїв. Розрахунки показують, що час релаксації електрона на дислокації виявляється обернено пропорційним до його швидкості, а його величина – на три порядка менша величини часу електрон-фононної релаксації. Тому (за винятком кристалів без домішкових атомів приT << TD) розсіюванням на дислокаціях можна нехтувати.
Іншим механізмом розсіювання, що може мати місце в напівпровідниках, зона провідності яких має не єдиний мінімум енергії у зоні Бріллюена, є так зване “міждолинне розсіювання“ – явище переходу електрона з одного мінімуму в інший. Такі переходи потребують значних змін квазіімпульсу електрона, можливих тільки внаслідок його взаємодії з високоенергетичним фононом, а тому, за винятком випадку дуже високих температур, малоймовірні.
Уже зазначалося, що при високій густині електронного газу можлива реалізація механізму електрон-електронного розсіювання. Проте, як показують розрахунки, навіть у випадку сильно вироджених напівпровідників і металів внесок електрон-електронного розсіювання у значення рухливості залишається неістотним порівняно з впливом інших механізмів.

5.4. Електропровідність напівпровідників і металів
Дрейф електронів у кристалі викликає появу в ньому електричного струму, густина якого
|
|
|
r |
|
|
r |
|
r |
(5.11) |
|
|
|
|
j = -enuдр |
= enme E . |
||||||
Згідно |
із |
законом |
Ома |
у |
диференціальній, цеформіозначає, що |
питома |
||||
електропровідність кристалу, носіями струму в якому є електрони, |
|
|||||||||
|
|
|
s e = enme |
= |
e2 |
nt eрел , |
(5.12) |
|||
|
|
|
me* |
|||||||
|
|
|
|
|
|
|
|
|
|
|
а у випадку діркової провідності, – |
|
|
|
|
|
|
|
|||
|
|
|
s h = epmh = |
e2 |
|
pt hрел . |
(5.13) |
|||
|
|
|
mh* |
|||||||
|
|
|
|
|
|
|
|
|
||
Електропровідність напівпровідника визначається сумарним зарядом, перенесеним |
||||||||||
електронами і дірками, тому |
|
|
|
|
|
|
|
|||
|
|
|
s = s e +s h = e(nme + pmh ) , |
(5.14) |
||||||
однак при температурах нижчих Ti може переважати провідність тільки одного(n або p) типу.
Значення часу релаксації електрона і дірки, очевидно, відрізняються навіть у одному і тому ж напівпровіднику, так що у випадку властивої провідності
s i = e(nme + pmh ) .
Вважаючи, що в області низьких температур рухливості носіїв пропорційні доТ3 (з коефіцієнтами пропорційності Ae,h), одержуємо
|
|
|
k B |
|
|
3 / 2 |
(m*m* ) 3 / 4 |
|
|
|
- |
Eg |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
s |
i |
= 2e( |
|
) |
( A |
+ A |
)T 3e 2kBT . |
|
|
(5.15) |
|||||||||
|
|
|
|
|
|||||||||||||||
|
|
2p h |
2 |
|
|
e |
h |
|
|
e |
h |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При малих значеннях температур таких, що kBT << Eg функція exp(- |
Eg |
) |
змінюється із |
||||||||||||||||
2k BT |
|||||||||||||||||||
зміною Т значно сильніше, аніж Т3. Тому, |
|
|
|
|
|
|
|
|
|
|
|||||||||
позначивши множник перед експонентою в |
|||||||||||||||||||
(5.15) символом σ0, можна записати |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
- |
Eg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kBT , |
|
|
|
|
|
|
|
||||
|
|
|
|
|
s i |
= s 0e |
|
|
|
|
|
|
(5.16) |
||||||
де σ0 – слабко залежна від температури величина.
В області високих температур рухливості носіїв пропорційні доТ-3/2, так що σ0 стає точно постійною величиною. Отже, формула для визначення температурної залежності властивої електропровідності напівпровідника має вигляд(5.16) для будь-яких температур. Графік цієї залежності наведений схематично на . рис5.3 (ділянка, що відповідає T > Ti).
Опір напівпровідника обернено пропорційний його електропровідності ,і відповідно до (5.16), експоненціально спадає при збільшенні температури:
Eg
R = R0e 2kBT ,
де R0 – практично постійна величина.
Для напівпровідників з домішковою провідністю, наприклад n-типу, електропровідність також експоненціально залежить від температури при T < Ts:
(5.17)
питома
|
|
|
|
|
|
- |
Ed |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kBT , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
s n = s 0n e |
|
|
|
|
|
|
|
|
|
(5.18) |
|
|||||
де σ0n |
– також |
слабко |
залежна |
від |
температури |
величина. При |
Ts |
< T < Ti |
|
||||||||||||
електропровідність зменшується при зростанні температури, оскільки в цій області |
|
||||||||||||||||||||
концентрація електронів у зоні провідності не збільшується, а розсіювання на фононах |
|
||||||||||||||||||||
зростає. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Графік залежності σn від температури наведений схематично на рис. 5.3 (ділянка, що |
|
||||||||||||||||||||
відповідає T < Ti). Зауважимо, |
що графік залежностіlnσ |
від 1/T має вигляд прямої , |
з |
|
|||||||||||||||||
кутовим |
коефіцієнтом –E/(2kB), |
де E |
= Eg |
у випадку |
властивої |
провідності , а |
для |
|
|||||||||||||
домішкової E = Ed. |
|
|
|
|
|
У |
|
випадку |
металів |
|
концентрація |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
електронного |
|
газу |
|
|
не |
|
залежить |
від |
||||||
|
|
|
|
|
|
|
температури. |
|
|
Тому |
|
температурна |
|
||||||||
|
|
|
|
|
|
|
залежність електропровідності визначається |
|
|||||||||||||
|
|
|
|
|
|
|
змінами рухливості. У кристалах високої |
|
|||||||||||||
|
|
|
|
|
|
|
чистоти (без домішок і дефектів) рухливість |
|
|||||||||||||
|
|
|
|
|
|
|
електронів |
|
аж |
до |
|
|
області |
|
низьки |
||||||
|
|
|
|
|
|
|
температур |
визначається |
|
їх |
розсіюванням |
|
|||||||||
|
|
|
|
|
|
|
на фононах, |
тобто μ ~ 1/T. Відповідно |
і |
|
|||||||||||
|
|
|
|
|
|
|
електропровідність |
металів |
|
виявляється |
|
||||||||||
|
|
|
|
|
|
|
обернено |
пропорційною |
до |
абсолютної |
|
||||||||||
|
|
|
|
|
|
|
температури, |
а |
опір – |
лінійно |
зростає |
при |
|
||||||||
|
|
|
|
|
|
|
збільшенні температури. Відома формула |
|
|
||||||||||||
Рис. |
5.3. |
Температурна |
|
залежніст |
|
|
|
|
|
r = r0 (1 +at) , |
|
(5.19) |
|
||||||||
|
описує |
температурну |
залежність |
питомого |
|
||||||||||||||||
електропровідності напівпровідника (крива σn |
|
||||||||||||||||||||
опору металу. Тут t – температура у шкалі |
|
||||||||||||||||||||
відповідає області домішкової, а σі – властивої |
|
||||||||||||||||||||
провідності) |
|
|
|
|
|
Цельсія, |
|
α |
– |
температурний |
|
коефіцієнт |
|
||||||||
|
|
|
|
|
|
|
опору, а ρ0 – значення опору при 0 °С. |
TD) |
|
||||||||||||
|
|
|
|
|
|
|
|
В |
|
області |
низьких(близько |
|
|||||||||
|
|
|
|
|
|
|
температур |
|
|
концентрація |
|
|
фононів |
||||||||
|
|
|
|
|
|
|
пропорційна до Т3, тому довжина вільного |
|
|||||||||||||
|
|
|
|
|
|
|
пробігу |
|
|
електронів, |
обумовлена |
|
їх |
|
|||||||
|
|
|
|
|
|
|
розсіюванням на фононах, пропорційна до |
|
|||||||||||||
|
|
|
|
|
|
|
Т-3. При цих температурах середній імпульс |
|
|||||||||||||
|
|
|
|
|
|
|
фононів дуже малий порівняно з імпульсом |
|
|||||||||||||
|
|
|
|
|
|
|
електронів, які рухаються з швидкістюυF. |
|
|||||||||||||
|
|
|
|
|
|
|
Тому |
|
для |
|
суттєвої |
|
зміни |
|
імпульсу |
||||||
|
|
|
|
|
|
|
електрона, що приведе до зміни напрямку |
|
|||||||||||||
|
|
|
|
|
|
|
його руху, потрібна взаємодія не з одним, а |
|
|||||||||||||
|
|
|
|
|
|
|
з більшою кількістю фононів . Виконані в |
|
|||||||||||||
Рис. |
5.4. |
Температурна |
|
залежніст |
рамках |
|
квантової |
|
теорії |
розсіювання |
|||||||||||
електропровідності провідника (горизонталь- |
розрахунки |
|
показують, |
що |
|
кількість |
|
||||||||||||||
на ділянка відповідає області залишковогофононів, |
необхідних |
|
для |
|
ефективного |
|
|||||||||||||||
опору) |
|
|
|
|
|
|
розсіювання |
|
електрона, |
залежить |
|
від |
|
||||||||
температури кристалу – пропорційна до Т-2. З цієї причини ефективна середня довжина |
|
||||||||||||||||||||
вільного пробігу і, відповідно, рухливість електронів, а тому й електропровідність металу |
|
||||||||||||||||||||
виявляються |
пропорційною |
до Т-5. Отже, в |
області |
|
низьких |
температур питомий |
опір |
|
|||||||||||||
металів змінюється пропорційно до Т5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При T → 0 концентрація фононів настільки мала, що довжина вільного пробігу |
|
||||||||||||||||||||
електрона |
стає |
сумірною |
з |
розмірами |
кристалу. Це |
мало |
|
би |
означати, що |
|
|||||||||||

електропровідність |
металу поблизу абсолютного нуля температур стає надзвичайно |
||||
великою, а опір – |
практично відсутній. Насправді ж, як показують експериментальні |
||||
вимірювання, |
опір |
металів не зникає приT → 0, а наближається до деякої постійної |
|||
величини – залишкового опору. Існування залишкового опору пояснюється розсіюванням |
|||||
на |
дефектах |
ґратки, яке при T → 0 стає найімовірнішим. Внесок цього механізму |
|||
розсіювання |
у |
рухливість, відповідно, електропровідність |
визначається |
тільки |
|
концентрацією дефектів, а тому постійний для кожного кристалу. |
|
|
|||
|
Залежність електропровідності твердого тіла від його температури використовується |
||||
для |
виготовлення терморезисторів. Зазвичай терморезисторами |
називають пристрої, |
|||
здатні істотно |
змінювати свій опір при зміні температури. Однією з основних |
||||
характеристик терморезистора є його температурний коефіцієнт опору – величина |
|
||||
a = 1 dR , R dT
що має зміст відносної швидкості зміни опору при зміні температури.
Згідно з уявленнями про природу електропровідності температурний коефіцієнт опору терморезистора, побудованого на його основі,
a = - B T 2
(5.20)
напівпровідни,
(5.21)
від’ємний (тут В – постійна, значення якої визначаються властивостями напівпровідника). Для виготовлення терморезисторів з від’ємним температурним коефіцієнтом опору(їх
називають термісторами) |
використовують |
суміші |
окислів |
перехідних |
металів |
|
(наприклад, Mn, Со, Ni, Cu); Ge і Si з різними домішками; карбід кремнію (SiC); |
||||||
напівпровідникові |
сполуки |
елементівIII і V |
груп; |
синтетичний |
алмаз; органічні |
|
напівпровідники і т.д. |
|
|
|
|
|
|
Існують також |
терморезистори з додатним |
температурним коефіцієнтом опору(їх |
||||
називають позисторами). Їх виготовляють на основі титанату барію BaTiO3 з домішками лантану, церію, вісмуту, або кремнію з домішками бору. Вказані сполуки при досягненні певної температури здатні змінювати свої електричні властивості– переходять у фазу сегнетоелектриків. В області температури фазового переходу їх опір різко зростає, що й забезпечує додатні значення α.
Терморезистори використовують для створення систем і пристроїв дистанційного і централізованого вимірювання або регулювання температури, протипожежної сигналізації і теплового контролю, температурної компенсації різних елементів електричних ,кіл
вимірювання вакууму та швидкості протікання рідин і , газівтакож вимірювачів потужності.
5.5. Надпровідність
У 1911 році голландський фізик Гайке Камерлінґ Оннес дослідним шляхом встановив стрибкоподібне зникнення опору ртуті при температурі4,2 К. Це явище отримало назву надпровідності і на даний час спостерігається у багатьох речовинах–
чистих |
металах |
та |
їх |
сплавах, інтерметалічних |
сполуках |
та |
ряді |
вироджених |
|||
напівпровідників. Струм, |
викликаний у |
колі, |
виготовленому |
з |
таких матеріалів, може |
||||||
існувати практично нескінченно довго. |
|
|
|
|
|
|
|
||||
Зникнення опору не могло бути пояснене відомими на той час теоріями |
|||||||||||
електропровідності, |
оскільки: |
1) навіть |
у |
металах |
з |
ідеальною |
ґраткою він мав |
||||
зменшуватись до нуля плавно, а не стрибкоподібно; 2) надпровідність була зареєстрована у реальних кристалах, з домішками і дефектами. Тому процес зникнення опору вважається фазовим переходом у специфічний стан– надпровідний. При переході у надпровідний
стан спостерігається різка аномалія електричних, магнітних, теплових та інших властивостей речовини. Це дає підстави вважати його як особливий стан речовини, що реалізується при температурах, нижчих так званоїкритичної температури явка
позначається символом Тк; у різних речовинах вона має значення від декількох сотих до
20 К.
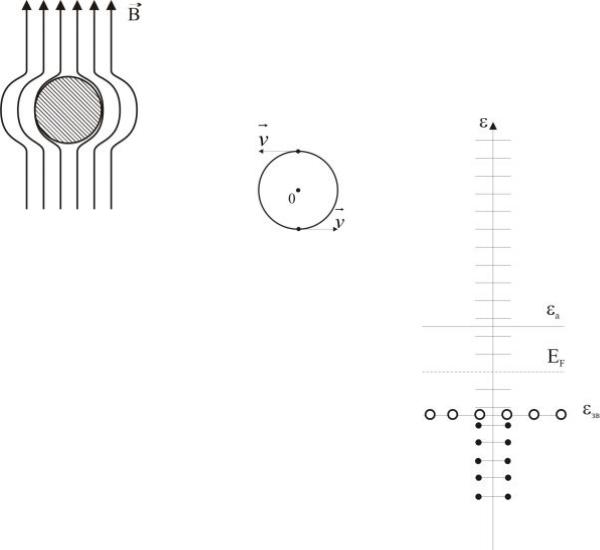
Зокрема, надпровідний стан характеризуєтьсяідеальним діамагнетизмом – властивістю, яка полягає в тому, що нижче температури Тк магнітна проникність речовини набуває нульового значення– магнітне поле “виштовхується” з об’єму надпровідника незалежно від того, вносять у нього надпровідник (рис. 5.5), чи переводять у надпровідний стан тіло, розташоване в ньому. Це явище називається ефектом Мейсснера-Оксенфельда.
Ідеальний діамагнетизм надпровідників свідчить про те, що струми у них протікають тільки по поверхні(інакше всередині них існувало би магнітне )поле. Розрахунки показують, що струми у надпровідниках протікають у приповерхневих шарах, товщина яких, залежно від матеріалу і температури, становить 10 – 100 нм.
Можливість переходу речовини у надпровідний стан пояснили у 1957 році Бардін, Купер і Шріффер. Згідно уявленням, розвиненим у їхній теорії, при T < Tк електрони можуть притягуватись, утворюючи нові квазічастинки– пари зв’язаних електронів (куперівські пари), що обертаються навколо миттєвого центра (точка О на рис. 5.6).
Рис. 5.5. Виштовху- |
|
|
|
|
|
|
|
|
|
|
|
|||
вання магнітного |
поля |
|
|
Рис. 5.6. |
Купе- |
|
|
|
|
|||||
з надпровідної кулі |
|
|
|
|
|
|
|
|||||||
|
|
|
рівська пара |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Миттєвий центр обертання може рухатись, що |
|
|
|
|
||||||||||
трактується як поступальний рух куперівської пари у |
|
|
|
|||||||||||
кристалі. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Утворення куперівських пар можна уявити як |
|
|
|
|||||||||||
наслідок збудження (при T < Tк) коливань атомів ґратки |
|
|
|
|
||||||||||
(позитивно |
заряджених |
іонів) |
напрямленим |
|
рухом |
|
|
|
|
|||||
електронів. |
Збуджені |
таким |
|
чином |
|
|
фонони |
|
|
|
|
|||
нерівноважними, а тому – |
нестабільними. Для переходу |
|
|
|
|
|||||||||
ґратки у рівноважний стан, енергія утвореного фонона |
|
|
|
|
||||||||||
повинна бути передана іншому електрону. Оскільки |
|
|
|
|
||||||||||
досягнення |
надпровідності |
реалізується |
|
у |
процесі |
|
|
|
||||||
охолодження |
|
|
|
|
|
|
|
|
|
|
|
|
||
кристалу, така передача здійснюється практично |
|
|
|
|
||||||||||
миттєво. |
Внаслідок обміну |
між |
електронами(через |
|
|
|
|
|||||||
фононну систему) |
енергія |
одного з них зменшується на |
Рис. 5.7. Положення основного і |
|||||||||||
величину |
енергії |
збудженого |
ним |
фонона, а |
іншого – |
збудженого |
рівнів куперівської |
|||||||
зростає |
|
порівняно |
з |
початковим |
|
значенням |
у |
|
|
|||||
рівноважному стані електронної системи. |
|
|
|
пари |
у енергетичному спектрі |
|||||||||
|
|
|
електрона провідності |
|
||||||||||
Це ж означає появу нових її станів – з меншою, ніж |
Жирними |
точками |
позначено |
|||||||||||
початкова, та з більшою |
енергіями . |
Зрозуміло, |
що у |
неспарені |
електрони, |
кружеч- |
||||||||
виродженій |
електронній |
системі |
металу зміни |
енергій ками – куперівські пари |
||||||||||
можливі тільки у електронів, які знаходяться поблизу поверхні Фермі, тому основний рівень зв’язаного стану εзв знаходиться нижче, а збуджений – εа, – вище рівня Фермі
(рис.5.7).
Стан з меншою енергією безумовно має бути заселений електронами, внаслідок їх нерозрізненості, – обома, тільки з протилежно напрямленими спіновими моментами. При
цьому енергія пари електронів, що знаходяться на нижньому рівні, менша суми їх енергій до взаємодії, коли вони були вільними. Отже, можна стверджувати, що обмін між
електронами через фононну систему приводить до утворення зв’язаного стану пари електронів, тобто взаємодія між ними має характер притягання.
У результаті обміну втрати енергії відсутні, тому сума енергій станів, утворених в результаті взаємодії має бути рівною сумі енергій одноелектронних станів до взаємодії. Це означає, що енергетичний рівень εа збудженого стану куперівської пари знаходиться вище рівня Фермі. Тому цей стан нестабільний – перевід куперівської пари на рівень εа буде супроводжуватись спонтанними переходами на вільні одноелектронні рівні нижче рівня Фермі, що означає розпад пари(з цієї причини стан з енергієюεа називається
антизв’язуючим).
При T < Tк одно електронні стани з енергією , більшою ніж εзв, також стають нестабільними – електронам енергетично вигідніше утворити пару і перейти на рівеньεзв. Для куперівських пар це можливо, оскільки вони є бозонами – сумарний спіновий момент спарених електронів дорівнює нулю. Зрозуміло, що відстань між рівнями εзв і εа буде тим більшою, чим більша концентрація куперівських пар.
Втеорії Бардіна-Купера-Шріффера показано, що протягування електронів з
утворенням |
куперівських |
пар буде ефективним, якщо вони володіють рівними за |
величиною, |
але протилежно |
напрямленими імпульсами. Ця умова виконується в будь- |
який момент часу, а пара не розпадається, якщо електрони здійснюють обертальний рух навколо спільного центра (рис. 5.6). Розрахунки показують, що просторова протяжність хвильової функції нового стану– куперівської пари, є досить великою: близько 103 нм, тоді як період ґратки сягає декількох нм . Тому хвильові функції різних пар можуть перекриватися між собою, а це приводить до корельованості (узгодженості) їх руху в кристалі. Згідно положень квантової механіки корельованість можлива квазічастинками, що перебувають в однакових станах. Для куперівських пар ця умова виконується, оскільки вони є бозонами. Одним із проявів корельованості куперівських пар є той факт, що зменшити їх кількість тим важче, чим більша їх концентрація– цьому опирається уся система спарених електронів. Єдиним шляхом для зменшення кількості куперівських пар є перевід однієї з них у станεа з подальшим розпадом на два неспарених електрона. З цього і випливає твердження про залежність від концентрації куперівських пар.
При 0 < T < Tк куперівські пари можуть розпадатися внаслідок розсіювання на теплових коливаннях ґратки з одночасним утворенням нових. Між цими протилежними процесам встановлюється динамічна рівновага, так що у металі завжди існує певна рівноважна кількість куперівських пар і неспарених електронів. Оскільки рівноважна концентрація куперівських пар залежить від температури кристалу, то ширина щілини є спадною функцією Т. Зокрема (Тк) = 0.
Наслідком наявності щілини в енергетичному спектрі електронів є факт відсутності електричного опору при T < Tк. Як відомо, він пояснюється розсіюванням електронів при кожному акті якого змінюються їх імпульс і/або .енергіяЗбільшити енергію, не розірвавши зв’язку з іншим електроном куперівської пари, електрон не може – для цього потрібний запас енергії не менший. Отримати таку енергію внаслідок електронфононної взаємодії при низьких температурах неможливо. При T < Tк. концентрація і енергія теплових коливань ґратки надзвичайно . маліЗа відсутності зовнішнього електричного поля сумарний імпульс куперівських пар дорівнює нулю внаслідок їх корельованості. За наявності ж поля, усі пари одержують однаковий імпульс, оскільки вони знаходяться в однакових станах, а тому рухаються в одному напрямку з однаковою швидкістю – виникає електричний струм. На відміну від неспарених електронів, жодна з куперівських пар не може змінити свого імпульсу. Тому довільна його зміна у одного з спарених електронів повністю компенсується зміною імпульсу другого , такщоби їх сумарний імпульс не змінювався. З цієї причини куперівські пари(квазічастинки з
