
FTT-stud / view4
.pdfРОЗДІЛ 4. СТАТИСТИКА ВІЛЬНИХ НОСІЇВ ЗАРЯДУ У КРИСТАЛАХ
4.1. Розподіл носіїв за енергією
Нескладно |
переконатися |
в |
,томущо |
у |
стані |
термодинамічної |
рівноваги |
одноелектронні стани, аналогічно до фононних, нерівномірно розподілені за значеннями |
|||||||
їх енергії. Дійсно, у наближенні |
ефективної |
|
маси енергія електрона у |
зоні |
|||
r |
|
|
|
|
|
|
|
e(k ) = h2 k 2 / 2m* внаслідок квантування компонент хвильового вектора |
|
||||||
k |
x |
= |
2p |
n , k |
y |
= |
2p |
n |
2 |
, k |
z |
= |
2p |
n |
3 |
|
|
|||||||
|
|
|
|
|
||||||||||||||||||||
|
|
Lx |
1 |
|
|
|
Ly |
|
|
|
|
|
Lz |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(тут Lx∙Ly∙Lz∙= Ω – об’єм кристалу, а n1, n2, n3 – цілі числа) визначається формулою |
||||||||||||||||||||||||
|
|
e |
n |
= |
|
|
h2 |
|
|
(n2 |
+ n |
2 |
+ n |
2 ) , |
|
|
|
(4.1) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2m* L2 |
1 |
|
|
|
2 |
|
3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
де для простоти покладеноLx = |
Ly = Lz = L, |
а |
|
номер рівня |
у зоніn |
визначається |
||||||||||||||||||
комбінацією значень квантових |
|
|
чисел(n1, |
n2, |
n3). |
Значення |
енергії ε1 |
= h2/2m*L2 |
||||||||||||||||
досягається при шести комбінаціях квантових чисел : (±1, 0, 0), (0, ±1, 0), (0, 0, ±1),
наступне значення, ε2 = h2/m*L2, – при дванадцяти: (±1, ±1, 0), (±1, 0, ±1), (0, ±1, ±1), а ε3 = 3h2/2m*L2 – при дев’яти і т.д. Отже, рівні ε1, ε2 і ε3 – шести-, дванадцятита дев’ятикратно вироджені, тоді як основний, ε0, - невироджений. Цей факт дозволяє говорити про нерівномірність розподілу одноелектронних станів за енергією.
Для характеристики розподілу одноелектронних станів за енергією зручно, як і у випадку фононів, використати поняття щільності розподілу станів за енергією – функції g(ε), добуток якої на величинуdε визначає кількість станів, значення енергії яких містяться у інтервалі (ε, ε + dε). Крім того, слід взяти до уваги, що електрони належать до групи ферміонів – частинок, які підпорядковуються принципу Паулі. Ймовірність знаходження такої частинки у стані з енергієюε визначається функцією розподілу Фермі-
Дірака
f (e) = |
1 |
|
(4.1) |
||
exp( |
e - m |
) +1 |
|||
|
|
||||
|
|
|
|||
k BT
(тут μ – параметр закону розподілу, відомий у статистичній фізиці під назвоюхімічний потенціал). За означенням, кількість заселених станів, енергія яких належить інтервалу (ε, ε + dε), становить величину g(ε)f(ε)dε.
Знання функцій g(ε) і f(ε) дозволяє знайти ряд характеристик електронної системи кристалу, наприклад середню енергію електрона в ньому. Дійсно, загальна кількість станів, заселених електронами
¥ |
|
N = ò g(e) f (e)de , |
(4.2) |
-¥ |
|
середня енергія системи електронів у кристалі |
|
¥ |
|
Ee = òeg(e) f (e)de , |
(4.3) |
-¥ |
|
а середня енергія одноелектронного стану –
¥
òeg(e) f (e)de
e |
= |
-¥ |
. |
(4.4) |
|
||||
|
¥ |
|
|
|
ò g(e) f (e)de
-¥
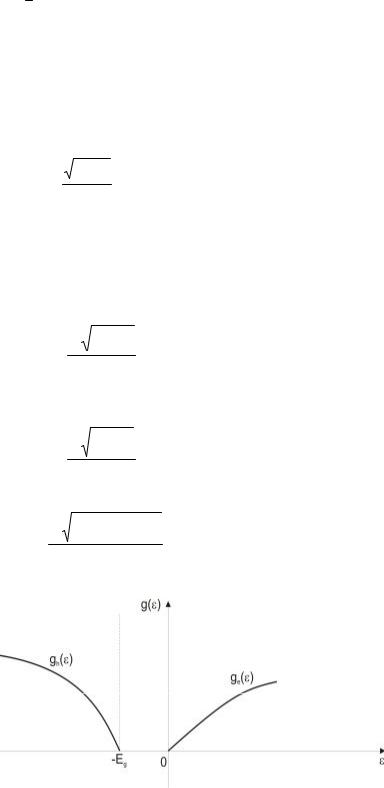
Явний вигляд функції g(ε) залежить від структури енергетичної зони і тому різний у різних кристалах, а в окремо взятому кристалі – у різних зонах. Найпростіший вигляд вона має у випадку параболічних зон, закон дисперсії яких має вигляд (3.47). У цьому випадку енергія електрона залежить від модуля хвильового вектора, так що усі стани з енергієюε знаходяться на поверхні сфери k-простору, радіус якої
k = 2m*e |
(4.5) |
h |
|
(тут для простоти відлік енергії ведеться від дна зони ). Стани, енергія яких належить інтервалу (ε, ε + dε), знаходяться всередині шару між двома концентричним сферами з радіусами k та k + dk (див рис. 2.7), а їх кількість, згідно (2.26), становить величину Ωk2dk/π2 (тут враховано також можливість знаходження на одному рівні двох електронів з протилежно напрямленими спіновими моментами). Переходячи від змінноїk до ε, з означення щільності розподілу станів за енергією знаходимо
|
|
|
|
|
g(e ) = |
W 2m*3e |
. |
|
(4.6) |
||
|
|
|
|
|
p 2h |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
||
Зокрема, |
якщо відлік енергії здійснювати від дна зони |
провідності(Ec = |
0), то |
||||||||
щільність розподілу для електронів провідності у напівпровіднику |
|
|
|||||||||
|
|
|
|
|
ge (e) = |
W 2me*3e |
, |
|
(4.7) |
||
|
|
|
|
|
p 2h |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
||
а дірок – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gh (e) = |
W 2mh*3 (Ev |
- e) |
|
(4.8) |
||
|
|
|
|
|
|
p 2h3 |
. |
|
|||
|
|
|
|
|
|
|
|
|
|
||
Графіки залежності g(ε) наведені на рис. 4.1. |
|
|
|
|
|
||||||
Функція розподілу Фермі- |
|
|
|
|
|
|
|||||
Дірака |
у |
якості |
параметрів |
|
|
|
|
|
|
||
містить |
дві |
величини |
– |
|
|
|
|
|
|
||
абсолютну |
|
температуру |
|
|
|
|
|
|
|||
системи |
Т |
та |
її |
хімічний |
|
|
|
|
|
|
|
потенціал μ. В області низьких |
|
|
|
|
|
|
|||||
температур |
(таких, |
|
що |
|
|
|
|
|
|
||
kBT < |ε – μ|) її |
значення мало |
|
|
|
|
|
|
||||
відрізняються |
від |
одиниці |
при |
|
|
|
|
|
|
||
ε < μ та від нуля при ε > μ і ці |
|
|
|
|
|
|
|||||
відмінності тим менші, чим |
|
|
|
|
|
|
|||||
нижча |
|
|
|
температура). |
|
|
|
|
розподілу за |
енер |
|
|
|
|
|
|
Рис. 4.1. Залежність щільності |
||||||
Апроксимуючи |
|
поведінкуелектронів провідності ge(ε) та дірок gh(ε) у напівпровіднику |
|||||||||
залежності f(ε) до абсолютного |
|
|
|
|
|
|
|||||
нуля температур, можна стверджувати, що при Т = 0 К |
|
|
|||||||||
|
|
|
|
|
ì1, |
якщо e |
< m; |
|
(4.9) |
||
|
|
|
|
|
f (e ) = í |
якщо e |
> m. |
|
|||
|
|
|
|
|
î0, |
|
|
||||

З цього факту випливає, що при Т = 0 одноелектронні стани, енергія яких більша ніж значення хімічного потенціалу, незаселені.
Значення енергії, що відділяє заселені при температурі абсолютного нуля рівні від
незаселених, у |
фізиці твердого тіла називаєтьсяенергією або рівнем Фермі. Очевидно, |
|||||
положення |
|
рівня |
|
ФерміEF |
|
|
визначається |
значенням |
хімічного |
|
|||
потенціалу μ, а саме – EF = μ при Т = 0 |
|
|
||||
К. |
|
|
|
|
|
|
При Т > 0 частинки знаходяться |
|
|
||||
у тепловому русі, енергія якого тим |
|
|
||||
більша, чим вища температура. Отже, |
|
|
||||
зростання |
|
температури |
означає |
|
||
можливість заселення рівнів, вищих |
|
|
||||
рівня Фермі на величину порівняну з |
|
|||||
енергією |
теплового |
рухуkT, що |
Рис. 4.2. Рівноважний |
розподіл електронів |
||
приводить |
до |
зміни |
розподілу(рис. |
енергією при Т = 0 (а) та Т > 0 (б) |
||
4.2). |
|
|
|
|
|
|
4.2. Відмінність законів розподілу у металах і напівпровідниках |
||||||
|
|
r |
|
|
поверхню k-простору, яка |
|
Рівняння |
e(k ) = EF визначає |
відокремлює повністю |
||||
зайняті (при Т = 0) одноелектронні стани від незаповнених. У наближенні квадратичного
закону дисперсії це – сфера, радіуса kF = 2me*EF |
і об’єму |
4 |
pkF3 (сфера Фермі). |
|
|||
h |
3 |
|
|
На кожний одноелектронний стан припадає елементарний об’єм(2π)3/Ω, так що їх
4p kF3 W
кількість під сферою Фермі 3(2p )3 . Ці стани заповнені електронами (по два на кожному рівні), концентрація яких у кристалі-провіднику визначається енергією Фермі
n = kF3 |
= ( 2me*EF )3 |
(4.10) |
3p 2 |
3p 2h3 |
|
іне залежить від температури. У металах ця величина набуває значень 1025 ... 1026 м-3.
З(4.10) одержується формула для оцінки величини енергії Фермі у провідниках
|
h2 |
|
|
EF = |
|
(3p 2n)2 / 3 . |
(4.11) |
2m* |
|||
|
e |
|
|
Вважаючи n = 5∙1025 м-3, а me* рівною масі спокою вільного електрона, отримуємо EF ≈ 5 еВ. Тоді середня енергія електрона провідності у металах
|
EF |
EF |
3 |
||
e |
= òe g(e)de : ò g(e)de = |
|
EF ≈ 3 еВ, |
||
5 |
|||||
0 |
0 |
|
|||
а середня швидкість руху вільних електронів у металах u = 2e / me* ≈ 106 м/c.
Одержані значення енергій є надзвичайно великим для мікрочастинки. Для того, щоби молекули ідеального газу володіли такою енергією, його необхідно нагріти до температури близько 25000 К. Це означає, що в області нормальних температур у металах рівність (4.9) виконується з ймовірністю, практично рівною одиниці (закон розподілу у такому випадку називають виродженим). З цієї причини електронний газ у металах також називають виродженим.
Підвищення температури провідника приводить до зміни розподілу електронів за енергією – відбувається їх перехід на незаповнені рівні вище рівня Фермі, хоча й з малою ймовірністю (f(ε) << 1 при ε > EF). Це приводить до того, що хімічний потенціал системи електронів у провіднику стає залежним від температури. З умови незмінності кількості електронів провідності можна отримати наближений вираз, що описує температурну залежність хімічного потенціалу
m(T ) = EF [1 - |
1 |
( |
pk BT |
) |
2 |
] , |
(4.12) |
3 |
2EF |
|
|||||
|
|
|
|
|
|
де EF визначається виразом (4.11). Як видно з (4.12), зростання температури приводить до зменшення хімічного потенціалу провідника, проте, внаслідок великих значеньEF такі зменшення несуттєві – навіть при кімнатних температурах μ(Т)/μ(0) ≈ 0,9999.
У напівпровіднику функція розподілу електронів провідностіf (e) » exp( m -e ) kBT
експоненціально спадає при збільшенні енергії стануε (якщо відлік енергії проводиться від дна зони провідності, то μ < 0), так що практично для усіх рівнів зони провідності за звичайних умов виконується умова невиродженості
|
|
f (e) <<1 . |
|
|
|
(4.13) |
||||||
З цієї причини електронний газ у напівпровіднику, |
іноді і |
сам кристал, називають |
||||||||||
невиродженим. |
|
|
|
|
|
|
|
|
|
|
|
|
Повна функція розподілу невиродженого електронного газу |
|
|
|
|
||||||||
|
|
W 2m*3 |
|
m |
|
- |
e |
|
|
|
|
|
f (e )ge (e) = |
|
|
|
k BT |
(4.14) |
|||||||
e |
e kBT e e |
|||||||||||
|
|
p 2h3 |
|
|
|
|
|
|
|
|
|
|
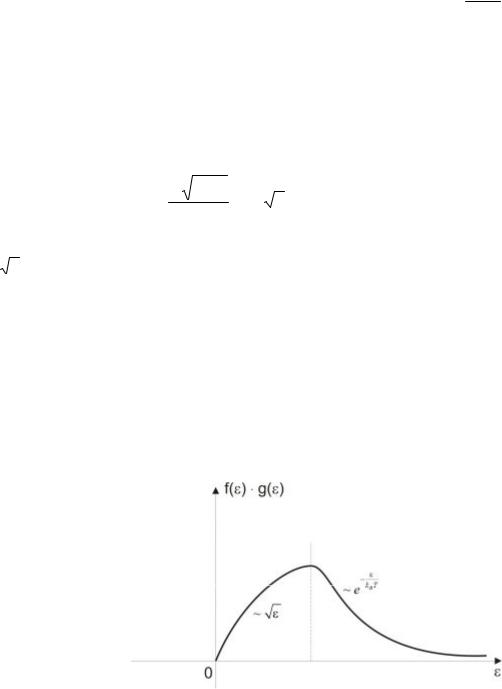
має немонотонну залежність відε: в області дна |
|
зони |
провідності вона |
зростає |
||||||||
пропорційно до e , а при великих значеннях енергії – спадає пропорційно до exp(- |
e |
|
) |
|||||||||
|
|
|||||||||||
(рис. 4.3). Це дозволяє обчислити концентрацію електронів як |
|
kBT |
||||||||||
|
|
|
|
|||||||||
|
1 |
¥ |
|
|
|
|
|
|
|
|
|
|
n = |
|
ò f (e)ge (e)de , |
|
|
|
|
|
|
|
|||
W |
|
|
|
|
|
|
|
|||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
що після інтегрування набуває вигляду
|
m*k |
|
T |
|
|
m |
|
m |
|
|
|
|
B |
)3/ 2 |
×e kBT |
= Nc e kBT , |
|
||||||
n = 2( |
e |
|
(4.15) |
||||||||
2p h2 |
|||||||||||
|
|
|
|
|
|
|
|
||||
де Nc – величина, яку називають ефективною кількістю станів зони провідності.
З (4.15) видно, що концентрація електронів провідності у напівпровіднику залежить від сорту кристалу (ним визначається значення хімічного потенціалу) та його температури – зростає при її збільшенні.
Ймовірність |
того, що |
|
|
одноелектронний |
стан |
|
|
енергією |
ε |
незаселений, |
|
визначається функцією |
Рис. 4.3. Характер енергетичної залежності функції f(ε)ge(ε) |
||
|
|
|
|
fh (e) =1- f (e ) = |
1 |
|
, |
(4.16) |
||
exp( |
m -e |
) +1 |
||||
|
|
|
||||
|
|
|
|
|||
kBT
яку слід вважати функцією розподілу дірок. Очевидно, для глибоких рівнів валентної зони також виконується умова невиродженості закону розподілу дірок(fh(ε) << 1), а їх концентрація
|
mh* k BT |
|
|
- |
m+Eg |
- |
m+Eg |
|
|
p = 2( |
) |
3/ 2 |
k T |
k T |
, |
(4.17) |
|||
|
|
×e |
B |
= N ve |
B |
||||
|
2p h2 |
|
|
|
|
|
|
|
|
де Nv – величина, яку називають ефективною кількістю станів валентної зони. Як і у випадку електронів, концентрація дірок визначається характеристиками напівпровідника (μ, Eg) та його температурою T.
Формули (4.15, 17) дозволяють встановити значення ширини забороненої зони та енергії Фермі електронного газу у досконалому напівпровіднику, також залежність концентрації вільних носіїв заряду від Eg. Дійсно, вільні носії заряду (електрони і дірки) з’являються в ньому парами, а тому ni = pi (індекс і означає, що розглядається властива провідність напівпровідника). Тоді розглядаючи (4.15) і (4.17) як систему рівнянь відносно концентрацій, одержимо
|
|
|
|
|
|
|
- |
Eg |
|
kBT |
|
3 / 2 |
|
3 / 4 |
- |
Eg |
|
|
|
n |
= p |
= |
N |
c |
N |
v |
× e 2kBT |
= 2( |
) |
(m*m* ) |
×e 2kBT |
– |
(4.18) |
||||||
|
|
|
|||||||||||||||||
i |
i |
|
|
|
|
|
|
2p h2 |
|
e h |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
концентрація вільних носіїв у досконалому напівпровіднику визначається його типом (через характеристики кристалу – ширину забороненої зони, ефективні маси електрона і дірки) та температурою. Зазначимо, що формула (4.18) одержана з використанням закону розподілу Фермі-Дірака, який виконується за умови термодинамічної рівноваги в системі електронів. З цієї причини вільні носії заряду, що з’являються завдяки тепловому збудженню системи електронів у напівпровіднику, та їх концентрації, визначені формулою (4.18), називаються рівноважними. Оскільки при малих температурах множник перед експонентою в (4.18) залежить від Т слабше, ніж експонента, то можна вважати, що рівноважна концентрація електронів і дірок у досконалому напівпровіднику залежить від температури за законом
E g
-
n (T ) = p |
(T ) = A ×e 2k BT , |
(4.19) |
|
i |
i |
|
|
де А – постійна величина.
Прирівнявши праві частини(4.15) і (4.17), одержуємо рівняння для знаходження хімічного потенціалу, звідки
|
Eg |
|
3 |
|
m* |
|
|
m(T ) = - |
|
+ |
|
kBT ln |
h |
, |
(4.20) |
|
|
me* |
|||||
2 |
|
4 |
|
|
|
||
а EF = μ(0) = – Eg/2 (рівень Фермі електронів у досконалому напівпровіднику відповідає середині забороненої зони).
З (4.20) видно також, що у випадку me* < mh*, що має місце у більшості випадків , хімічний потенціал електронної системи досконалого напівпровідника зростає при його нагріванні пропорційно до абсолютної температури, а при me* > mh* – зменшується.
4.3. Статистика вільних носіїв у домішкових напівпровідниках
У випадку напівпровідників з домішками або дефектами кристалічної ґратки (наприклад, вакансіями) вільні носії заряду можуть з’являтися також внаслідок переходів
з локальних рівнів(донорних або акцепторних) у стани валентної зони або зони провідності. Кількість вільних носіїв заряду, викликаних переходами за участю певного локального рівня у забороненій зоні, пропорційна до кількості домішкових центрів або дефектів, що спричинили появу даного рівня. Крім того, як і у випадку зонних станів, заселеність рівнів електронами у стані термодинамічної рівноваги визначається функцією розподілу. Закон розподілу описується функцією, подібною до функції розподілу ФерміДірака
¢ |
1 |
|
, |
(4.21) |
|
|
|
|
|||
f (e ) = |
g ×exp( |
e¢ - m |
) +1 |
||
|
|
|
|
||
kBT
де ε΄ – енергія рівня, а g – фактор виродження, – множник, значення якого залежить від природи локального рівня. Зокрема, у випадку мілких рівнів донорного типуg = 1/2, акцепторних – g = 2. Очевидно, рівноважна концентрація електронів, локалізованих на енергетичному рівні донорного або акцепторного типу, дорівнює добутку концентрації відповідних домішкових центрів на функцію розподілу (4.21).
Розглянемо мілкий донорний рівень з глибиною заляганняEd, створений домішковими атомами, концентрація яких Nd. За умови настільки малих температур, що появою властивої провідності можна знехтувати, кількість електронів у зоні провідності напівпровідника практично повністю визначається кількістю звільнених в результаті переходу до неї місць на домішковому рівні, тобто Nd[1 – f(-Ed)]. З іншого боку, вважаючи,
що електрони в зоні провідності |
утворюють невироджений електронний(це газ |
||||||||||||
справедливо при малих концентраціях домішкових |
|
атомів), їх концентрацію можна |
|||||||||||
знайти, подібно до випадку |
досконалого |
напівпровідника, за |
формулою (4.15). |
||||||||||
Прирівнюючи названі величини, отримуємо |
рівняння |
для |
знаходження хімічного |
||||||||||
потенціалу напівпровідника n-типу |
|
|
|
|
|
|
|
|
|
||||
|
m*k |
B |
T |
)3/ 2 exp( |
m |
|
|
N |
d |
|
|
||
2( |
e |
|
|
) = |
|
|
. |
(4.22) |
|||||
2p h2 |
kBT |
|
Ed |
|
|||||||||
|
|
|
|
|
+ m |
|
|
||||||
|
|
|
|
|
|
|
2 exp( |
|
|
|
) +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k BT
Знайти розвозок рівняння(4.22) можливо тільки чисельними методами, проте у ряді граничних випадків це можна зробити й аналітично. Розглянемо їх детальніше.
При Т → 0 донорні центри слабко іонізовані, концентрація електронів, що з’явилися
у зоні провідності внаслідок переходу з рівня одновалентної домішки, |
|
||||||||||||||||||||||
|
nd = |
|
|
|
|
|
N d |
|
|
|
|
<< N d . |
|
||||||||||
|
|
|
|
|
|
Ed + m |
|
|
|
|
|||||||||||||
|
|
|
|
|
2 exp( |
) +1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
k BT |
|
|
|
|
|
|
|
|
|
|
|
||
Виконання цієї нерівності |
можливе |
за умови2 exp( |
Ed |
|
+ m |
) +1 >> 1 . Тоді (4.22) |
можна |
||||||||||||||||
|
|
|
|||||||||||||||||||||
подати у вигляді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k BT |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp( |
m |
) = |
N d |
( |
2p h2 |
)3/ 2 exp(- |
|
Ed |
) , |
(4.23) |
|||||||||||||
kBT |
|
|
|
me*kBT |
|
|
|||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
k BT |
|
||||||||||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m(T ) = - |
Ed |
+ |
k BT |
ln[ |
N d |
( |
2p h2 |
|
)3/ 2 ]. |
(4.24) |
|||||||||||||
|
|
|
me*k BT |
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|||||||
Другим доданком у (4.24) при Т → 0 можна знехтувати, так що m(0) º EF = - |
Ed |
– рівень |
|
2 |
|||
|
|
Фермі у напівпровіднику n-типу знаходиться посередині між донорним рівнем і дном зони провідності.
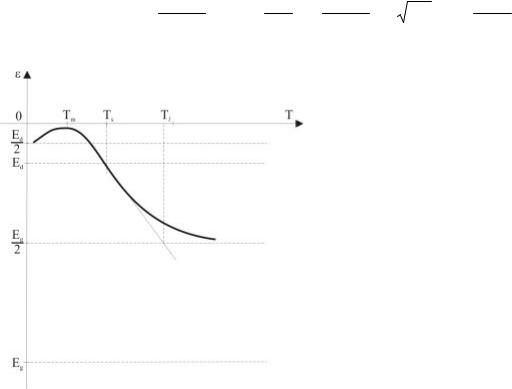
Згідно (4.24), зростання температури приводить до зсуву хімічного потенціалу на шкалі енергій за рахунок зростання величини другого доданку. Його зміни із збільшенням температури немонотонні – він нелінійно зростає до тих пір, поки me*kBT < 2πħ2, досягає максимуму у точці Tm = 2πħ2/(me*kB), а потім – зменшується. Відповідно змінюються і значення хімічного потенціалу (рис. 4.4), який у точці Ts досягає значення μ = − Ed, так що подальші переходи з донорного рівня неможливі . З цієї причини Ts називається
температурою виснаження домішкового рівня.
Для оцінки величини Ts використаємо (4.22) вважаючи множник перед експонентою у лівій частині слабко залежним від температури(це можливо, оскільки ми працюємо у припущенні низьких температур). Тоді для температури виснаження домішкового рівня одержується вираз
Ts = |
Ed |
, |
(4.25) |
||
k B ln |
3Nc |
||||
|
|
|
|||
|
N d |
|
|
||
|
|
|
|
||
з якого видно, що величина Ts залежить від характеристик кристалу, типу і кількості домішкових атомів у ньому – me*, Ed, Nd. Зокрема, впровадження атомів As у кристал Ge приводить до утворення донорних рівнів з глибиною залягання0,01 еВ. Ефективна маса електрона у зоні провідності такого напівпровідника становить 0,23m0 при концентрації Nd = 4,7∙1021 м-3. Розрахована за формулою (4.25) температура виснаження домішкового рівня цієї системи становить 28 K.
Відповідно до (4.24), за умови T < Ts рівноважна концентрація електронів у зоні провідності, які перейшли з донорного рівня, визначається температурою кристалу і глибиною залягання рівня:
nd (T ) = 2( |
me*kBT |
) |
3/ 2 |
exp( |
m |
) = ( |
me*kBT |
) |
3/ 4 |
N d exp(- |
Ed |
) , |
|
2p h |
2 |
|
k BT |
2p h2 |
|
2k BT |
|||||||
|
|
|
|
|
|
|
|
|
|||||
або, аналогічно до (4.19),
Рис. 4.4. Температурний зсув хімічного потенціалу електронів у напівпровіднику n-типу
|
|
|
|
|
|
- |
Ed |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nd (T ) = Bd e 2kBT , |
|
|
|
|
(4.26) |
|||||||||
де Вd |
– практично |
|
незалежна |
від |
|||||||||||
температури |
величина, |
значення |
|
якої |
|||||||||||
залежить від типу кристалу, домішки та її |
|||||||||||||||
концентрації, |
а Еd |
– |
глибина |
|
залягання |
||||||||||
донорного рівня. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При |
|
температурах, |
вищих |
|
Ts, |
||||||||||
донорний рівень практично іонізований, |
|||||||||||||||
усі електрони здійснили перехід з |
нього |
||||||||||||||
до зони провідності, а тому |
|
можна |
|||||||||||||
вважати, |
що |
nd = Nd, |
звідки |
|
|
визначаємо |
|||||||||
температурну |
|
|
залежність |
|
|
хімічного |
|||||||||
потенціалу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m(T ) = kBT ln[ |
N d |
( |
2p h2 |
) |
3/ 2 |
]. |
(4.27) |
||||||||
2 |
me*kBT |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
Аналіз |
формули (4.27) |
|
показує, |
що |
|||||||||||

зростання температури від значенняTs приводить до майже лінійного зменшення хімічного потенціалу. У околі температури збудження властивої провідностіTі (рис. 4.4) швидкість зміни хімічного потенціалу зменшується, а його значення наближаються до величини, характерної для досконалого напівпровідника.
Температура збудження властивої провідності визначає граничні умови теплового режиму роботи напівпровідникових пристроїв. Величину Tі можна оцінити припустивши, що при її досягненні у зоні провідності зрівнюються концентрації електронів, збуджених переходами з валентної зони і з домішкового рівня, тобто ni(Ti) = nd(Ti). Звідси
Ti |
= |
Eg |
|
. |
(4.28) |
|
|
||||
|
|
k B ln( Nc Nv / N d2 ) |
|
||
Підставляючи у одержану формулу значення |
величин, характерних |
для германію і |
|||
кремнію при концентраціях домішкових атомів близько1022 м-3, одержуємо Tі ≈ 500 K (Ge)
і Tі ≈ 680 K (Si).
Зауваження. 1. У випадку домішки-акцептора усі висновки, описані вище, також залишаються справедливими з тією різницею, що хімічний потенціал системи електронів має протилежний напрямок температурного зсуву (рис. 4.5).
Рис. 4.5. Температурний зсув хімічного потенціалу у напівпровіднику p-типу
Концентрація дірок у валентній при T < Ts залежить від температури законом, подібним до (4.26):
зоніРис. 4.6. Заселеність рівнів компенсованого |
|
за |
напівпровідника при Т = 0 |
|
|
- Ea |
|
pa (T ) = Ba e 2kBT , |
(4.29) |
де Ва – практично незалежна від температури величина, значення якої залежить від типу кристалу, домішки та її концентрації, а Еа – глибина залягання акцепторного рівня.
2. Часто у напівпровідниках присутні як донорні, так і акцепторні домішкові центри. Їх присутність зменшує домішкову провідність одного типу (електронну або діркову) кристалу. З цієї причини такі напівпровідники називаютьсякомпенсованими. За умови рівної кількості валентних електронів атомів-донорів і місць на акцепторних рівнях приT = 0 домішки обох типів іонізуються, електрони заселять найнижчі дозволені енергетичні
рівні у забороненій зоні(рис. 4.6), а кристал буде поводити себе як досконалий з властивим типом провідності.
4.4. Рівноважний розподіл вільних носіїв заряду за швидкостями |
|
|
|
||||||||||||
Робота |
твердотільних |
електронних |
|
пристроїв |
ґрунтується |
|
на |
я |
|||||||
електропровідності, надпровідності та інших, пов’язаних з особливостями руху вільних |
|
||||||||||||||
носіїв заряду у зовнішніх полях. Метою даного розділу є ознайомлення з сучасними |
|
||||||||||||||
уявленнями про природу названих явищ. Це можна зробити на основі викладеної у |
|
||||||||||||||
попередніх розділах інформації про будову енергетичного спектра фононів і електронів, а |
|
||||||||||||||
також статистичних закономірностях, яким підпорядковується рух цих квазічастинок. |
|
||||||||||||||
Досягнення поставленої мети можливе за умови формування уявлення про особливості |
|
||||||||||||||
руху і взаємодії квазічастинок у кристалах, зокрема розподіл електронів по швидкостях. |
|
|
|||||||||||||
Для |
знаходження |
закону |
розподілу |
|
|
вільних |
носіїв |
заряду |
по |
швидкос |
|||||
використаємо знайдений вище їх розподіл за енергією у досконалому напівпровіднику. |
|
||||||||||||||
Відповідно до означення функції розподілу за енергією та (4.14), кількість електронів, що |
|
||||||||||||||
володіють енергією в інтервалі (ε, ε + dε) у зоні провідності, становить величину |
|
|
|
||||||||||||
|
|
|
W 2me*3 |
|
m |
- |
e |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
e |
k |
T |
k |
T |
de . |
|
(4.30) |
|
||||
|
f (e )ge (e)de = |
2h3 |
B |
|
e e |
B |
|
|
|
||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
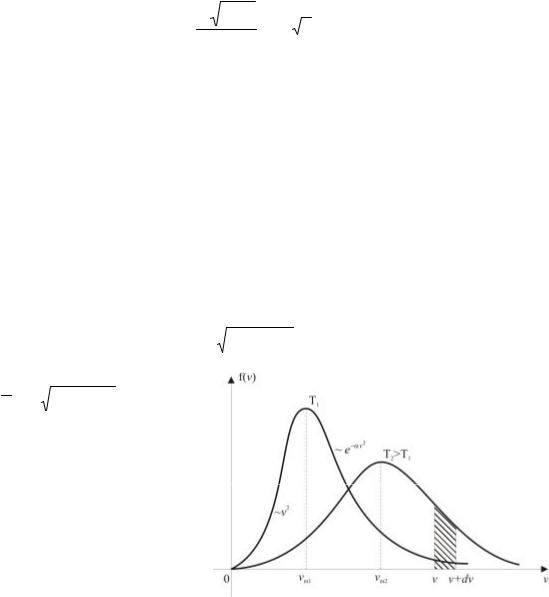
Вважаючи, що повна енергія електрона провідностіε = me*υ2/2, з (4.30) отримується концентрація електронів, швидкість руху яких належить інтервалу (υ, υ + dυ):
|
|
|
m*u2 |
|
|
|
m* |
- |
e |
|
|
|
2kBT 4pu 2du . |
|
|||
dn =n( |
e |
)3/ 2 e |
(4.31) |
||
|
|||||
u |
2p kBT |
|
|
|
|
|
|
|
|
|
|
Тут n – їх рівноважна |
концентрація, що визначається |
формулою(4.15). |
|||
Співвідношення (4.31) являє собою розподіл електронів провідності у напівпровіднику за значеннями їх швидкостей з щільністю розподілу Максвелла
|
|
|
|
|
m*u2 |
|
|
|
|
|
me* |
|
|
- |
e |
|
|
|
|
f (u) =( |
|
3/ 2 |
2k T |
|
2 |
|
|
||
|
) |
|
e |
B |
4pu |
|
. |
(4.32) |
|
|
|
|
2p k BT
Як видно, швидкість руху електронів провідності може набувати довільного значення, проте з різною ймовірністю. Найімовірніша
|
|
|
|
|
|
|
|
|
|
um = 2kBT / me* |
|
та середньоквадратична |
|
|
|
|
|||||||
|
|
u |
кв |
= |
3k |
B |
T / m* |
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
||
швидкості |
|
|
|
теплового |
|
|
|||||
визначаються |
|
ефективною |
масою |
||||||||
електрона, |
що |
є |
|
характеристикою |
|
||||||
системи, |
і |
|
температурою |
кристалу |
|
||||||
(зростає |
пропорційно |
до T1/2 при її |
|
||||||||
збільшенні). Оцінка, |
виконана |
за |
|
||||||||
умови me* = m0 при T = 300 K свідчить, |
|
||||||||||
що |
швидкість |
|
руху |
електрона |
|
||||||
напівпровіднику |
становить |
величину |
|
||||||||
того ж порядку, що |
й |
швидкість |
|
||||||||
вільних |
електронів |
|
у |
металах, – |
106 |
Рис. 4.7. Щільність розподілу електронів провідності |
|||||
м/с. |
|
|
|
|
|
|
|
|
|
|
невиродженого напівпровідника за швидкостями |
|
При швидкостях, значно менших |
(площа заштрихованої смуги дорівнює ймовірності |
|||||||||
від |
υm, |
функція |
|
(4.32) |
зростає, |
попадання швидкості електрона у інтервал (υ, υ + dυ) |
|||||
пропорційно до υ2, а при υ >> υm – експоненціально спадає (рис. 4.7).
Відповідно, відстань між сусідніми дозволеними значеннями однойменної
компоненти його швидкості дорівнюєh/(me*Li), так що деякій виділеній множині швидкостей {(υx, υx + dυx), (υy, υy + dυy), (υz, υz + dυz)} відповідає 2Ωdυxdυydυz/(h/me*)3 станів
(з урахуванням їх спінового виродження). Беручи до уваги, що заповнення станів невиродженого електронного газу підпорядковується розподілу Больцмана з щільністю
|
|
|
|
|
|
|
|
|
|
m-e |
|
|
|
|
|
m |
- |
me* |
(ux2 +uy2 +uz2 ) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
f (e) = e kBT = e kBT e 2kBT |
|
|
, |
|
|
|
|
|
|||||||||||||||||||
знаходимо концентрацію електронів, що |
|
володіють |
|
швидкостями |
з |
вказаної області |
||||||||||||||||||||||||||
значень |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
me* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
- |
|
(ux2 +uy2 +uz2 ) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dnux ,uy ,uz |
=n( |
me |
|
|
) |
3/ 2 |
e |
|
2kBT |
|
|
|
|
|
dux du y duz = |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2p k BT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
m*u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
me*u2y |
|
|
|
|
|
m*u2 |
|||||
|
|
m* |
- |
e x |
|
|
|
m* |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
m* |
- |
|
e z |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
=n[( |
|
e |
)1/ 2 e 2kBT dux ] ×[( |
|
|
|
|
e |
|
|
)1/ 2 e 2kBT du y ] ×[( |
e |
)1/ 2 e 2kBT duz ] . |
|||||||||||||||||||
2p k BT |
2p kBT |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2p k BT |
|
|
|
|
||||||||||
Компоненти |
вектора |
швидкості |
|
|
|
електрона |
провідності– незалежні випадкові |
|||||||||||||||||||||||||
величини, тому кожний з виразів у |
|
|
|
прямокутних дужках являє собою ймовірність |
||||||||||||||||||||||||||||
попадання υi |
у інтервал (υi, υi + dυi). Це означає, що функція |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m*u2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
me* |
|
|
|
|
|
|
- |
e |
i |
|
|
|
|
|
|
||||
|
|
|
|
|
|
f (ui ) =( |
|
|
|
|
1/ 2 |
|
2kBT |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
e |
|
|
|
|
|
|
(4.33) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2p kBT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
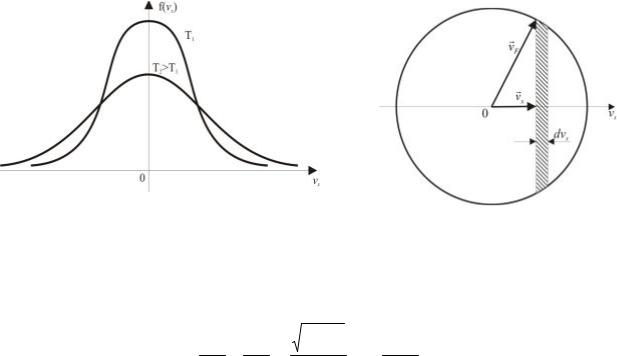
є щільністю розподілу електронів провідності невиродженого напівпровідника іза-ою компонентою вектора швидкості(i= x, y, z); її графік – гауссова крива, – схематично поданий на рис. 4.8.
Рис. 4.8. |
Щільність |
розподілу |
ронів |
|
провідності |
невиродженого |
напівпровідника |
за |
|
значеннями проекції швидкості υx |
|
Рис. 4.9. |
||
У випадку провідників електронний газ вироджений і при T =0 усі стани аж до рівня Фермі повністю заповнені, отже щільність розподілу електронів за швидкостями дорівнює густині станів
|
n |
|
1 |
EF |
*3 |
e |
|
*3 |
|
|
f (u) = |
= |
|
2me |
de = |
2me |
, |
(4.34) |
|||
WF |
WF 0ò |
p 2h3 |
|
h3 |
||||||
де ΩF = 4πυF3/3 – об’єм сфери Фермі радіуса υF.
За умови υx < υF сфера Фермі відтинає від множини точок, що містяться між площинами υx = const i υx + dυx = const простору зміни швидкостей область(рис. 4.9), об’єм якої при малих значеннях dυx становить величину π(υF2 - υx2)dυx. Відношення цієї
