
FTT-stud / view7
.pdfРОЗДІЛ 7. КОНТАКТИ ТА ГЕТЕРОПЕРЕХОДИ
7.1. Особливості меж розділу середовищ
До цих пір нами розглядалися явища, спостережувані у практично однорідних твердих тілах, з досконалою у більшості випадків кристалічною ґраткою. До особливих випадків відносилися ґратки з дефектами типу вакансій, домішкових атомів, дислокацій і т.п. При цьому вважалося, що кристалічна ґратка, як це випливає з її означення, безмежна. Проте реальні кристали мають скінчені розміри, а при створенні на їх основі електронних приладів, вони входять до складу електричних , контактуючиіл з електродами, виготовленими з іншого матеріалу. Це означає, що у реальних умовах кристали мають суттєві дефекти ґратки – вільну поверхню або межу розділу середовищ. Поблизу вільної поверхні або межі розділу середовищ характер руху електронів і атомів кристалу істотно відрізняється від їхнього руху в безмежній ґратці. Виявляється, що у приповерхневій зоні
контактуючих матеріалів |
структура зонного |
спектру має |
суттєво інший вигляд, ніж у |
об’ємі, а це приводить до протікання у них особливих процесів– так званих контактних |
|||
явищ. Зазначені явища |
істотно впливають |
на фізичні |
властивості усієї структури і |
приводять до нових, надзвичайно важливих з практичної точки зору якостей.
Межі розділу двох різних матеріалів (в подальшому будемо називати її контактами) використовують не тільки для утворення з’єднань між елементами приладів, під’єднання їх до зовнішніх електричних кіл, але й для створення багатьох приладів: електронних (діодів, транзисторів, елементів інтегральних схем), термоелектричних (генераторів струму, пристроїв кондиціонування) та оптоелектронних (фотота світлодіодів, фото транзисторів, напівпровідникових лазерів).
З точки зору електричних властивостей контакти класифікуються як омічні, нелінійні або інжектуючі. Залежно від конкретного призначення контактів, до них ставляться певні вимоги. Так омічний контакт призначений для забезпечення провідності; він повинен володіти малим опором, не спотворювати форму сигналу, що передається через нього, не створювати у колі електричних шумів, його вольт-амперна характеристика повинна бути лінійною. Нелінійні контакти, призначенням яких є нелінійні перетворення електричних сигналів (випрямлення, детектування, модуляція, генерування і т.п.), навпаки повинен мати різко нелінійну вольт-амперну характеристику, зі спеціальними вимогами в кожному конкретному випадку. Інжектуючі контакти, призначені для інжектування (впорскування, примусового введення) неосновних носіїв тільки в одному напрямку, а тому властивості його повинні бути різко асиметричними; носії повинні пройти через
нього не встигнувши рекомбінувати. |
|
Наведена вище інформація не |
є вичерпною, проте ілюструє складність і |
різноманітність контактних явищ, розгляду |
яких і присвячується даний та наступні |
розділи. |
|
7.2. Емісія електронів з поверхні кристалу
Робота багатьох електронних приладів ґрунтується на явищіелектронної емісії – витоку електронів з кристалу через його поверхню. Наприклад, у електронно-променевих трубках кінескопів та електровакуумних лампах потік електронів від катода до анода
забезпечується вириванням електронів з поверхні катоду внаслідок його нагрівання(це |
|
||
явище називається термоелектронною емісією); у вакуумних фотоприймачах – за рахунок |
|
||
зовнішнього фотоефекту – явища виривання |
електронів з поверхні катода |
при |
його |
освітленні (його іноді називають фотоемісією). |
|
|
|
Електрони провідності знаходяться |
у кристалічному , щополі є |
для |
них |
потенціальною ямою (див. рис. 3.2 б). Вирватися з неї здатні тільки ті електрони, що знаходяться на “хвості” розподілу Фермі-Дірака при T > 0 (права частина графіка на рис. 4.2 б). Їх статистика добре описується функцією розподілу Больцмана
f (e) = exp(- |
e - m |
) |
(7.1) |
|
|||
|
k BT |
|
|
(тут μ < ε < 0), з чого випливає, що за умови ε >> EF існує відмінна від нуля ймовірність набуття електроном енергії ε > 0, тобто вирватися за межі кристалу.
Вивільнення електрона з кристала можливе за умови одержання ним додаткової енергії, необхідної для подолання потенціального бар’єру, яким є для нього поверхня кристалу. У обох наведених прикладах термоелектронної та фотоемісії електрони набувають необхідного запасу енергії за рахунок поглинання фонона ,абовідповідно, фотона.
Найменша величина запасу енергіїχ0, необхідної електронові для виривання з кристалу називається термодинамічною роботою виходу. Очевидно, у металах при 0 К термодинамічна робота виходу дорівнює різниці енергій вільного електрона(найменше її значення вважається рівним нулю) і енергії Фермі: χ0 = −EF. Для характеристики властивостей напівпровідника її відлік також ведеться від рівня Фермі, хоча у випадку невироджених напівпровідників він знаходиться у забороненій зоні і жодного електрона
на ньому не може бути. |
|
|
|
Е |
|
|
Різниця |
енергій вільного |
електрона |
і енергії |
дна зони |
називається |
|
|
|
|
|
|
провідності |
|
зовнішньою роботою виходу або спорідненістю до електрона; значення її χс = −Ес. |
||||||
Струм, |
обумовлений електронами, |
що вирвалися з кристалу внаслідок його |
||||
нагрівання або освітлення, називається |
струмом |
емісії (відповідно, |
термоабо |
|||
фотоелектронної). Розрахуємо |
струм |
емісії електронів |
з поверхні кристалу, що |
|||
знаходиться у стані термодинамічної рівноваги, виходячи з уявлень квантової статистики. Відповідно до принципу Паулі, координати і квазіімпульси мікрочастинок пов’язані
між собою так, що мінімальний об’єм, який може займати одна з них у просторі координат-квазіїмпульсів, становить
(Dpx × Dx)(Dp y × Dy)(Dpz × Dz) ³ h3 . |
(7.2) |
У випадку одиничного об’єму у просторі координат Dx × Dy × Dz = 1 ця умова набуває |
|
вигляду |
|
(Dpx × Dp y × Dpz ) ³ h3 . |
(7.3) |
Тоді кількість одноелектронних станівdz у одиниці об’єму, що характеризуються квазіімпульсами, компоненти яких належать інтервалам (px, px + dpx), (py, py + dpy) та (pz, pz + dpz), дорівнює
dz = 2 |
dpx dp y dpz |
= |
2(me* )3 |
|
dυx dυy dυz . |
(7.4) |
|||
h3 |
|
|
h3 |
|
|||||
|
|
|
|
|
|
|
|||
Концентрацію dn таких електронів знайдемо, помноживши кількість станів dz на |
|||||||||
ймовірність їх заповнення f(ε): |
|
|
|
|
|
|
|
|
|
|
|
2(m* )3 - |
e -m |
|
|
|
|||
|
|
|
|
|
|
||||
|
dn = |
|
e |
|
e kBT dυx dυ y dυz . |
(7.5) |
|||
|
h3 |
|
|||||||
|
|
|
|
|
|
|
|
||
Потік електронів, що вирвалися з поверхні кристалу, дорівнює їх кількості у елементі об’єму з одиничною площею основи і висотоюl = υz: dN = υzdn, а щільність струму емісії –
j = eò dN = eòυz dn = |
2e(me* )3 |
òòòexp(- |
e - m |
)υz dυx dυy dυz . |
(7.6) |
h3 |
|
||||
|
|
kBT |
|
||
Для обчислення щільність струму виразимо у(7.6) повну енергію електрона провідності через його швидкість υ
|
|
|
|
|
m*υ2 |
|
|
|
|
m* |
|
|
|
|
|
|
|
||
|
|
e = Ec |
+ |
|
e |
= Ec + |
e |
(υx2 + υ2y + υz2 ) . |
|
|
|
|
(7.7) |
||||||
|
|
|
2 |
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тоді для щільності струму отримуємо вираз |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
m*υ2 |
|
|
|
me*υ2y |
|
m*υ2 |
|
|
|
||
|
2e(me* )3 |
|
Ec |
- m |
¥ - |
e |
x |
|
¥ - |
|
¥ - |
e |
z |
|
|
|
|||
|
|
2k |
T |
|
2k T |
2k |
T |
|
|
|
|||||||||
j = |
|
exp(- |
|
|
|
) ò e |
|
B |
|
dυx òe |
B |
dυy ò e |
B |
|
uz dυz , |
(7.8) |
|||
h3 |
k BT |
|
|
|
|||||||||||||||
|
|
|
-¥ |
|
|
|
|
-¥ |
|
uz min |
|
|
|
|
|
||||
де перший і другий інтеграли |
виражаються |
|
|
|
|
|
|
¥ |
-x 2 dx = |
p , а |
|||||||||
через інтеграл Пуассонаe |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-¥ |
|
|
останній береться безпосередньо. У результаті для щільності струму термоелектронної емісії отримуємо вираз
j = AT 2 exp(- |
c0 |
) , |
(7.9) |
|
|||
|
k BT |
|
|
де враховано, що χ0 = −μ. Формула (7.9) називається формулою Річардсона – Дешмена, а
коефіцієнт A = 4πeme*kB2/h3 = (me*/m0)∙1,2∙106 A/(м2∙К2) – постійною Річардсона.
З (7.9) видно, що струм термоелектронної емісії визначається тільки роботою виходу кристалу і його температурою.
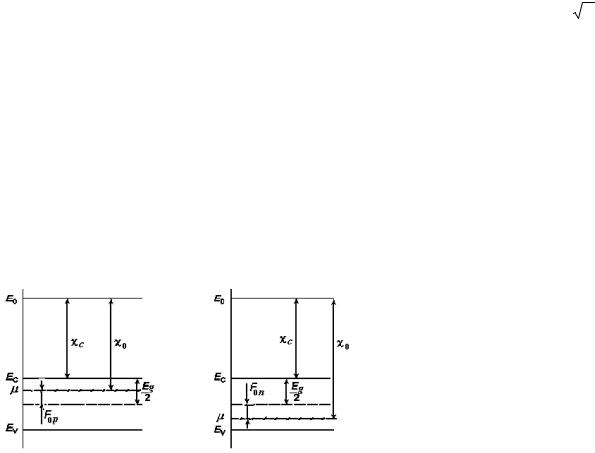
Розглянемо зонні діаграми напівпровідниківn- та p-типу, одержаних легуванням деякого кристалу відповідними домішками– донорами і акцепторами. Положення хімічного потенціалу в них будуть відрізнятися від його положення у досконалому напівпровіднику (рівня Фермі) на величину Fn або Fp відповідно (рис. 7.1).
Згідно означення термодинамічної роботи виходу, її величина у напівпровіднику n-типу
|
|
|
|
|
|
|
c |
0n |
= -m = c |
c |
+ |
|
Eg |
|
- F |
(7.10) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
n |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
більша від роботи виходу у з |
||||||||||||||
|
|
|
|
|
|
|
напівпровідника p-типу |
|
|||||||||||||
|
|
|
|
|
|
|
c0 p |
= -m = cc + |
|
Eg |
+ Fp . |
(7.11) |
|||||||||
а) |
|
|
б) |
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Відповідно |
|
|
|
|
|
|
і |
струм |
|||||||
Рис. 7.1. Зонні діаграми напівпровідників n- (а) та p- |
|
|
|
|
|
|
|
|
|
||||||||||||
|
термоелектронної емісії з поверхні |
||||||||||||||||||||
типу (б). |
|
|
|
|
|
|
|||||||||||||||
E0, Ec і Ev – енергії вільного електрона, дна зони провідності і |
|
напівпровідника |
|
з |
|
n-типу |
буде |
||||||||||||||
верха валентної зони; Eg – ширина забороненої зони; χс – |
|
більшим, |
ніж |
|
|
напівпровідника |
|||||||||||||||
спорідненість до електрона; χ0 – |
|
термодинамічна робота |
у |
p-типу при тій самій температурі. |
|||||||||||||||||
виходу; F0n і F0p – зміна положень |
хімічного |
потенціалу |
|
|
Якщо |
|
|
|
|
між |
емітером |
||||||||||
домішкових напівпровідниках відносно його положення у |
|
|
|
|
|
|
|||||||||||||||
електронів (катодом) і колектором |
|||||||||||||||||||||
досконалому кристалі при Т = 0 К |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
(анодом) |
створено |
|
гальмуючу |
|||||||||||
різницю потенціалів U < 0, то до анода зможуть дістатись тільки ті електрони , енергія |
|||||||||||||||||||||
яких перевищує величину χс – eU. У цьому випадку сила струму термоелектронної емісії |
|||||||||||||||||||||
I = AST |
2 |
exp(- |
cc |
- eU - m |
) = I0 exp( |
eU |
) |
|
|
|
|
|
|
|
|
(7.12) |
|||||
|
|
k BT |
kBT |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
стає експоненціально залежною від напруги U.
При U > 0 усі електрони, що емітували з поверхні катода, дістануться до анода. Відповідно до (7.9) їх кількість не залежить відU, а тому і сила струму термоелектронної емісії має бути постійною, рівною величині струму насичення I0 = jS (S – площа поверхні емітера). Проте, прискорююче зовнішнє електричне поле, сприяючи виходу електрона з

катода, зменшує потенціальний бар’єр на деяку величину (це явище називається ефектом Шотткі). Розрахунки показують, що величина зниження бар’єра у не дуже сильних полях пропорційна Е1/2. Ефект Шотткі є причиною того, що зростання позитивного потенціалу на колекторі струм емісії не зберігається постійним, рівним струмові насичення, а дещо збільшується.
7.3. Ефект поля
Розглянемо вплив зовнішнього електричного поля на розподіл вільних носіїв заряду у при поверхневій області напівпровідника. Для простоти будемо вважати, що поле створюється зарядженою металевою площиною з поверхневою густиною зарядуσ. Оскільки силові лінії електричного поля повинні бути замкнуті , то на поверхні
напівпровідника виникне рівний по величині заряд протилежного знаку. Залежно |
від |
||||||
знаку заряду на металевій площині, екрануюче поле заряду у приповерхневій області |
|||||||
напівпровідника буде мати різні напрямки (рис. 7.2). |
|
|
|
||||
Якщо поле напрямлене |
|
|
|
|
|||
від |
поверхні |
всередину |
|
|
|
|
|
напівпровідника (рис. 7.2 а), |
|
|
|
|
|||
то енергія |
електронів буде |
|
|
|
|
||
мінімальною |
біля |
поверхні. |
|
|
|
|
|
Це означає, що поверхня для |
|
|
|
|
|||
електронів |
провідності |
а) |
б) |
|
|
||
цьому |
випадку |
є |
|
|
|||
потенціальною ямою. |
Рис. 7.2. |
Зміни розподілу вільних |
носіїв |
заряду |
у- |
||
Зміна |
потенціальної поверхневій області напівпровідника n-типу під |
дією |
поля |
||||
енергії |
електронів |
внаслідок металевої площини, зарядженої а) позитивно, б) негативно |
|
||||
їх переміщення до поверхні |
z |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
DV = V (z) -V (¥) = ò E(z)dz , |
|
|
|
|
|
|
|
|
¥ |
|
|
|
де V(∞) – потенціальна енергія електронів у квазінейтральному об’ємі напівпровідника, z – координата електрона (його відстань від поверхні) всередині кристалу. Оскільки на дні зони провідності кінетична енергія електронів дорівнює нулю, то зміна потенціальної
енергії по координаті повинна так само змінити енергетичне положення дна зони провідності Eс та, відповідно, і верха валентної зони Ev. Такі зміни проявляються у згині енергетичних зон і є причиною згадуваних вище ефектів Франца – Келдиша та Шотткі.
У випадку збільшення концентрації вільних носіїв у приповерхневій області (рис. 7.2 а) кажуть, що має місце їїзбагачення; у протилежному (рис. 7.2 б) – збіднення. Явище
зміни концентрації вільних носіїв у приповерхневій області напівпровідника під дією
зовнішнього електричного поля називається ефектом поля. |
|
|
|
||||
Внаслідок |
ефекту |
поля |
приповерхнева |
область |
напівпровідника |
набу |
|
надлишкового |
заряду (позитивного |
чи негативного). |
Його |
називають просторовим |
|
||
зарядом, а саму область– |
областю |
просторового |
заряду. |
Електричне поле області |
|
||
просторового заряду змінює величину потенціальної енергії електрона. Величина різниці потенціалів між квазінейтральним об’ємом і довільною точкою області просторового заряду
j= 1 òz E(z)dz e ¥
називається електростатичним потенціалом цієї точки.
Значення енергії електростатичного поля на поверхні напівпровідника називається поверхневим потенціалом і позначається символомys (ys = eφs); його знак відповідає
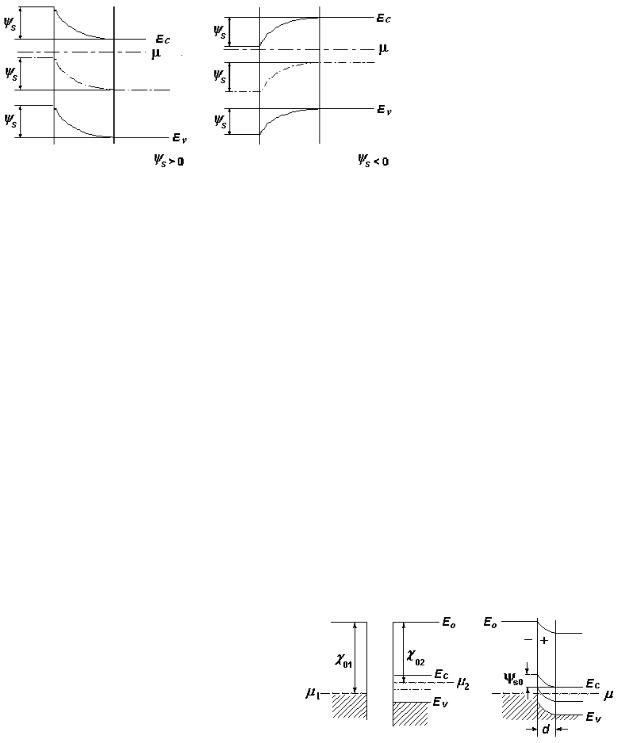
знакові заряду на металевому електроді, який викликає згин енергетичних зон. При ys > 0 зони зігнуті вниз, а при ys < 0 – вгору (рис. 7.3).
а) |
б) |
Рис. 7.3. Згин енергетичних зон напівпровідник n-типу у випадку збіднення (а) та збагачення (б) приповерхневої області
При малому збуренні електронної системи приповерхневої області напівпровідника (ys < kBT) електростатичний потенціал, а відповідно, й електричне поле всередині нього спадають за експоненціальним законом:
|
|
- |
z |
- |
z |
|
y(z) =y |
e |
|
|
|||
|
LD ; E(z) = E e LD , |
|||||
s |
|
|
|
s |
||
|
|
|
|
(7.13) |
||
де LD – так звана дебаївська довжина екранування – кількісна характеристика ефекту поля, що має зміст середньої глибини проникнення зовнішнього поля у кристал.
7.4. Контакт метал-напівпровідник
У випадку створення контакту метал – напівпроводник, можливі різні комбінації (p-
і n-типи напівпроводника) і співвдношення термодинамичних робіт виходу з металу і напівпровідника. Залежно від цих співвідношень в області контакту можуть реалізуватися три стани. Перший стан відповідає умові плоских зон у напівпровіднику; у цьому випадку
реалізується нейтральний контакт. Другий стан відповідає умові збагачення приповерхневої області напівпровідника основними носіями (електронами у n- і дірками у p-типі); уцьому випадку реалізується омічний контакт. Третій випадок – приповерхнева область напівпровідника виснежена на основні носії; у цьому випадку в області контакту з боку напівпровідника формується область просторового заряду іонізованих донорів або акцепторів і реалізується блокуючий контакт, який має найбільше практичне застосування у напівпровідниковому приладобудуванні.
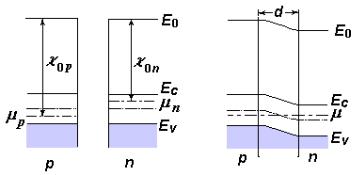
Розглянемо умови його виникнення на прикладі контакту металу з напівпровідником n-типу. Будемо вважати для визначеності, що термодинамічна робота виходу електрона з
металу χ01 |
більша, |
|
ніж з напівпровідникаχ02. Згідно |
(7.9) у цьому |
випадку |
струм |
|||||||
термоелектронної емісії з поверхні напівпровідникаj2 |
буде більшим струму емісії з |
||||||||||||
поверхні металу j1. |
|
|
показані |
зонні |
|
|
|
|
|||||
На |
рисунку 7.4 |
|
|
|
|
||||||||
диаграми |
етапів |
|
формування |
контакту |
|
|
|
|
|||||
метал – напівпровідник. |
У початковий |
|
|
|
|
||||||||
момент струм з напівпровідника у метал |
|
|
|
|
|||||||||
буде перевищувати зворотній струм з |
|
|
|
||||||||||
металу |
у |
|
|
|
напівпровідник; у |
|
|
|
|
||||
приконтактній |
|
|
області |
|
|
|
|
|
|
||||
накопичуватися |
|
|
об’ємні |
|
заряди– |
а) |
|
б) |
|
||||
негативні |
у |
металі, позитивні |
– |
у |
|
|
|||||||
Рис. 7.4. Зонні діаграми |
металу |
(1) і |
|||||||||||
напівпровіднику. |
Як |
наслідок, |
у |
області |
|||||||||
напівпровідника n-типу (2) а) |
до та б) після |
||||||||||||
контакту |
виникне |
електричне |
поле, |
що |
|||||||||
утворення контакту |
|
|
|||||||||||
приведе до згину енергетичних зон, а це, |
|
|
|||||||||||
|
|
|
|
||||||||||
у свою чергу, – до зростання термодинамічної роботи виходу з поверхні напівпровідника. Цей процес буде проходити до тих пір, поки хімічні потенціалиμ1 і μ2 контактуючих поверхонь не зрівняються і не встановиться рівновага. Між металом і напівпровідником

внаслідок ефекту поля виникне різниця потенціалівφк = ψs0/e = (χ01 – χ02)/e (її називають
контактною).
Вирівнювання хімічних потенціалів на межі розділу металу і напівпровідника
відбувається |
за рахунок перетікання електронів у метал |
з приконтктного ш |
|||
напівпровідника деякої товщини d (рис. |
7.4) і саме на нього припадає уся контактна |
||||
різниця потенціалів. Іонізовані атоми домішки, що залишилися в цьому шарі, утворюють |
|||||
область позитивного просторового заряду, де |
практично відсутні основні носії– |
||||
електрони. З |
цієї причини збіднений |
контакт |
метал– напівпровідник n-типу володіє |
||
високим електричним опором і називаєтьсяблокуючим. Блокуючі контакти іноді |
|||||
назвивають бар’єрами Шотткі. |
|
|
|
|
|
Розподіл |
r |
і потенціалуφ |
електричного поля |
всередині області |
|
напруженості E |
|||||
просторового |
заряду знайдемо |
з рівняння Пуассона. Спрямувавши вісь Oz від поверхні |
|||
вглиб напівпровідника, розглянемо одновимірний випадок рівняння Пуассона
¶2j(z) |
= - |
r(z) |
, |
¶z 2 |
|
||
|
ee0 |
||
r(z) – об’ємна густина заряду, ee0 – діелектрична проникність напівпровідника. У області просторового заряду напівпровідникаn-типу заряд
іонізованими атомами домішки-донора з концентрацією Nd, тому
(7.14)
створений
r(z) = qN d ,
r
де q – заряд домішки. Враховуючи зв’язок напруженості і потенціалу поляE подамо (7.14) у вигляді лінійного диференціального рівняння
dE = - qN d . dx ee0
(7.15)
=-Ñj ,
(7.16)
Вибираючи постійну інтегрування з умови, що на глибині d напруженість поля дорівнює нулю, отримуємо розв’язок
|
|
E(z) = |
qN d |
(d - z) , |
|
(7.17) |
|
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
ee0 |
|
|
|
|
||
аналіз якого показує, що напруженість поляЕ максимальна на |
межі метал– |
|
|||||||||
напівпровідник (z = 0), лінійно спадає в області просторового заряду і дорівнює нулю на |
|
||||||||||
межі цієї області з квазінейтральним об’ємом решти напівпровідника (z = d). |
|
|
|||||||||
Розподіл |
потенціалу |
по |
області |
просторового |
заряду |
знаходимо |
шлях |
||||
інтегрування (7.17) за умови j(d) = 0. Отримуємо, що потенціал поля бар’єрного контакту |
|
||||||||||
|
|
j(z )= |
qN d |
(d - z)2 . |
|
(7.18) |
|
||||
|
|
|
|
|
|||||||
|
|
|
|
2ee0 |
|
|
|
|
|||
зменшується за параболічним законом при заглибленні у напівпровідник. Аналогічно поводить себе і потенціальна енергія: зменшується до нуля на відстаніd від поверхні контакту; на межі розділу метал – напівпровідник вона набуває максимального значення ys0 = c01 - c02 (рис. 7.4 б). Підставляючи це значення у(7.18), знаходимо ширину області просторового заряду
d = 2ee0y s0 = |
2ee0jк , |
(7.19) |
e2nn0 |
enn0 |
|
де nn0 – концентрація основних носіїв у напівпровіднику n-типу (якщо q = e, то nn0 = Nd). Співвідношення (7.19) дуже важливе для аналізу бар’єрних структур. Воно має
універсальний характер і свідчить, що ширина області просторового заряду зростає при зростанні контактної різниці потенціалів і зменшується при збільшенні концентрації основних носіїв. Зокрема з нього можна знайти, що при контактній різниці потенціалів φк
= 1 В і концентрації електронівnn0 |
= 1020 м-3 |
у n-германії (ε |
= 10) ширина |
області |
|
||||||||||||
збіднення на межі контакту з металом становить 3∙мкм, а при nn0 = 1022 м-3 – 0,3 мкм. |
|
|
|||||||||||||||
|
Наявність потенціального бар’єру для електронів дає можливість створювати на |
||||||||||||||||
основі блокуючого бар’єра пристрої для випрямлення змінного струму– діоди Шотткі. |
|
||||||||||||||||
Детальніше це питання буде розглянуте у наступному розділі. |
|
|
|
|
|
|
|
|
|||||||||
|
Якщо термодинамічна робота виходу електрона з напівпровідникаn-типу більша, |
|
|||||||||||||||
ніж з металу, то при утворенні контакту між ними електрони будуть перетікати з металу у |
|
||||||||||||||||
напівпровідник. Енергія електрона при віддаленні його від |
поверхні |
розділу |
буде |
||||||||||||||
зростати, внаслідок чого викривлення зон буде відбуватися у напрямку, протилежному до |
|
||||||||||||||||
показаного |
на |
рис. 7.4 б (див. рис. 7.3 б), – створюється |
потенціальний бар’єр, що |
|
|||||||||||||
перешкоджає подальшому проникненню елктронів у напівпровідник. Після вирівнювання |
|
||||||||||||||||
хімічних потенціалів у приконтактному шарі глибини d утворюється область негативного |
|
||||||||||||||||
просторового |
заряду. |
Концентрація |
вільних |
електронів |
у |
|
приповерхневій |
області |
|||||||||
напівпровідника збільшується, відповідно зростає її електропровідність. Таку область |
|
||||||||||||||||
називають збагаченою, а контакт – неблокуючим. |
|
|
|
|
|
|
|
|
|
||||||||
|
Поблизу контакту метал – напівпровідник p-типу також |
можуть виникати |
області |
|
|||||||||||||
просторового |
заряду, |
збагачені |
|
основними |
носіями |
або |
збіднені, залежно |
від |
|
||||||||
співідношення величин роботи виходу. Зокрема блокуючий контакт утворюється тоді, |
|
||||||||||||||||
коли термодинамічна робота виходу з напівпровідника p-типу більша, ніж з металу. |
|
|
|
||||||||||||||
|
7.5. Електронно-дірковий перехід |
|
|
|
|
|
|
|
|
|
|||||||
|
Контакт бар’єрного типу утворюється також на межі розділу двох зразків |
|
|||||||||||||||
напівпровідникового матеріалу з різним типом провідності(електронним та дірковим). |
|
||||||||||||||||
Такі контакти називають електронно-дірковим або p – n-переходом. Найпоширенішими |
|
||||||||||||||||
прикладами p – n-переходів є такі, як n-Si – p-Si та n-Ge – p-Ge. |
|
|
|
|
|
|
|
|
|||||||||
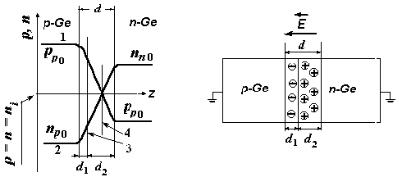
|
Нехай утворено контакт двох напівпровідників |
з різним типом провідності, |
|||||||||||||||
наприклад |
n-Ge |
– p-Ge. Через |
поверхню, яка |
розмежовує |
області |
з |
донорними |
і |
|||||||||
акцепторними домішками (її називають металургійним p – n-переходом) можливий обмін |
|
||||||||||||||||
електронами з напівпровідника n-типу (де вони є основними носіями) у напівпровідник p- |
|
||||||||||||||||
типу |
і навпаки – з |
напівпровідника p-типу (тут |
вони – неосновні, |
їх поява |
може |
бути |
|
||||||||||
викликана факторами стимулювання властивої провідності або наявністю домішок іншого |
|
||||||||||||||||
типу; важливо, що їх кількість значно менша, аніж кількість основних носіїв – дірок) у |
|
||||||||||||||||
напівпровідник n-типу. Оскільки термодинамічна робота виходу уp-Ge χ0p більша, ніж у |
|
||||||||||||||||
n-Ge χ0n (рис. 7.5 а), то згідно (7.10) і (7.11) контактна різниця поверхневих потенціалів |
|
|
|||||||||||||||
|
|
|
|
|
|
Dy s0 = c0 p - c0n = Fp + Fn > 0 , |
|
|
|
|
|
(7.20) |
|
||||
з чого випливає, що кількість елек- |
|
|
|
|
|
|
|
|
|
|
|
||||||
тронів, які переходять за одиницю |
|
|
|
|
|
|
|
|
|
||||||||
часу з напівпровідникаn-типу у |
|
|
|
|
|
|
|
|
|
|
|||||||
напівпровідник p-типу завжди буде |
|
|
|
|
|
|
|
|
|
|
|||||||
більшою, ніж зворотній потік. Отже з |
|
|
|
|
|
|
|
|
|
|
|||||||
приконтактної |
|
області |
напівпро- |
|
|
|
|
|
|
|
|
|
|||||
відника n-типу буде спостерігатися |
|
|
|
|
|
|
|
|
|
||||||||
відтік електронів у напівпровідник p- |
|
|
|
|
|
|
|
|
|
|
|||||||
типу, |
де |
вони |
рекомбінують |
|
|
|
|
|
|
|
|
|
|
||||
основними |
носіями – |
дірками. |
|
а) |
|
|
|
|
б) |
|
|
|
|||||
Аналогічно і з приконтактної області |
|
|
|
|
|
|
|
|
|||||||||
напівпровідника |
|
p-типу |
|
буде Рис. 7.5. Зонні діаграми |
напівпровідників p- і n-типу |
|
|||||||||||
спостерігатися |
|
відтік |
дірок |
до (а) та після (б) утворення контакту |
|
|
|
|
|
||||||||
|
у |
|
|
|
|
|
|
|
|
|
|||||||
напівпровідник n-типу, де вони рекомбінують з основними носіями– електронами. |
|
||||||||||||||||
Іншими словами, при створенні контакту напівпровідників з різним типом провідності |
|
||||||||||||||||
виникає емісійний |
струм |
через |
металургійнийp |
– n-перехід. |
При |
цьому |
існує |
чотири |
|
||||||||
компоненти струму – дві дифузійні і двідрейфові. Дифузійні компоненти обумовлені рухом основних, а дрейфові – неосновних носіїв.
Оскільки зовнішні джерела і стоки зарядів відсутні, то зміна розподілу зарядів у області контакту (рис. 7.6 а) не змінює електронейтральності системи, проте спричиняє появу внутрішнього електричного поля(іноді його називають дифузійним), яке протидіє взаємному переміщенню основних носіїв (рис. 7.6 б), та згин енергетичних зон по обидва боки контакту (ефект поля). При цьому на поверхні зразка p-типу термодинамічна робота виходу зменшиться, а у зразку n-типу – збільшиться. Термодинамічна рівновага буде
досягнута, |
коли |
|
емісійні |
|
|
|||
потоки |
носіїв |
з |
поверхонь |
|
|
|||
обох |
зразків |
|
|
зрівняються. |
|
|
||
При |
цьому |
|
|
зрівняються |
|
|
||
також і значення їх хімічних |
|
|
||||||
потенціалів (рис. 7.5 б), у |
|
|
||||||
приконтактному |
шарі зразку |
|
|
|||||
n-типу утвориться збіднена |
|
|
||||||
область |
просторового заряду |
|
|
|||||
позитивно |
|
|
|
іонізованих |
|
|
||
атомів-донорів, |
|
|
а |
у |
а) |
б) |
||
напівпровіднику |
|
p-типу |
– |
|||||
негативно |
|
|
|
іонізованихРис. 7.6. а) Розподіл концентації дірок (1) та електронів (2) у |
||||
акцепторів |
(рис. |
|
7.6 |
б). несиметричному p – n-переході; б) Схема p – n-переходу |
||||
Електропровідність |
областей |
3 – площина металургійного, а (4) – фізичного p – n-переходу |
||||||
просторового заряду, збіднених на вільні носії, мала. |
уp – n-переході, вважаючи, що |
|||||||
Розглянемо |
|
тепер |
процеси, |
що відбуваються |
||||
провідність напівпровідників викликана одновалентними домішками. У цьому випадку
положення |
хімічних потенціалів |
уn-і p-областях |
|
відносно |
рівня Фермі |
досконалого |
|||||||
кристалу |
задовольняють умовам jn < jp |
і за |
відсутності |
зовнішнього |
поля висота |
||||||||
потенціального бар’єра p – n-переходу буде становити величину |
|
|
|||||||||||
|
Dy |
s0 |
= F |
p |
+ F |
= |
k BT |
ln |
N a N d |
. |
|
(7.21) |
|
|
|
|
|
||||||||||
|
|
|
n |
|
e |
|
ni2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
Розподіл вільних носіїв заряду – електронів і дірок у p- та n-областях по обидва боки приконтактного шару шириною d (рис. 7.6) у припущенні їх електронейтральності має вигляд:
- p-область: концентрація основних носіїв (дірок) |
p p0 |
= ni exp( |
F0 p |
) = N a , |
|
|||||||||||
k BT |
(7.22) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
неосновних (електронів) – n p0 = ni exp(- |
F0 p |
) = |
ni2 |
; |
||||||||||||
k BT |
N a |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
- n-область: концентрація основних носіїв (електронів) |
nn0 = ni |
exp( |
F0n |
) = N d , |
||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
kBT |
|
(7.23) |
||||
|
|
|
|
|
|
|
|
|
|
n2 |
|
|||||
|
|
|
F |
|
|
|
|
|
|
|
||||||
неосновних (дірок) – pn0 |
= ni exp(- |
0n |
|
) = |
|
|
|
i |
|
|
|
|||||
kBT |
|
|
N d |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
(тут використано закон діючих мас: pp0np0 = nn0pn0 = ni2).
Для області просторового заряду p у– n-переході ці співвідношення трансформуються так, що F0p і F0n стають функціями, залежними від координат, Fp(z) і

Fn(z). Відповідно і концентрації носіїв у області просторового заряду також будуть функціями координат
p p (z) = ni exp( |
Fp (z) |
|
|
), n p |
|
|
||
|
k BT |
|
nn (z) = ni exp( Fn (z)), pn k BT
(z) = ni exp(- Fp (z)),
kBT (7.24) (z) = ni exp(- Fn (z)).
k BT
При заглибленні у область просторового заряду з боку напівпровідникаp-типу величина Fp зменшується майже лінійно (зростає хімічний потенціал), тому концентрація дірок pp буде при цьому експоненціально спадати при наближенні до ,точкиу якій значення хімічного потенціалу відповідають середині забороненої зони(множину таких точок називають фізичним p – n-переходом; на рис. 7.5 б це – точка перетину штрихової і штрих-пунктирної ліній). У точках фізичного p-n-переходу Fp = 0, а концентрація дірок досягає значення рівноважної концентрації носіїв для випадку властивої провідностіni. Концентрація ж електронів np навпаки – експоненціально зростає до значенняni у точці фізичного p – n-переходу (рис. 7.6 а).
Аналогічно змінюється концентрація основнихnn і неосновнихpn носіїв при заглибленні у область просторового заряду з боку напівпровідникаn-типу. Характер розподілу носіїв у несиметричномуp-n-переході (Na > Nd) разом зі схемою переходу показаний схематично на рис. 7.6, з якого можна побачити, що у несиметричних p – n- переходах фізичні і металургійні p – n-переходи просторово рознесені. Розподіл основних і неосновних носіїв симетричний відносно лінії, що відповідає концентрації властивої
провідності ni. |
його характеристик розглянемо рівняння Пуассона(7.14) |
|
Для |
знаходження |
|
сумістивши |
координатну |
площину xOy з площиною металургійногоp – n-переходу (її |
положення показане стрілкою 3 на рис. 7.6 а, а вісь Oz спрямуємо у бік напівпровідника n- типу.
Заряд області просторового заряду p – n-переходу, що відповідає z > 0 обумовлений наявністю іонізованих донорів з концентрацією Nd, а для z < 0 – іонізованих акцепторів з концентрацією Na, тому
r(z) = ìí- eN a , z < 0,
îeN d , z > 0.
Інтегруванням рівняння Пуассона знаходимо вирази для просторового розподілу напруженості
ì |
|
eN |
a |
(d1 |
||||
ï- |
|
|
||||||
|
|
|
||||||
ï |
|
ee0 |
||||||
E(z) = í |
|
|
eN d |
|
||||
ï |
- |
(d |
||||||
|
||||||||
ï |
|
|
ee |
0 |
|
|||
î |
|
|
|
|
|
|||
(знак мінус вказує напрям вектора напівпровідника p-типу) та потенціалу
+ z), - d1 < z < 0,
2 - z), 0 < z < d 2
напруженості– від
(7.25)
напівпровідника n-типу до
ì |
|
|
|
eN a |
(d1 |
+ z) |
2 |
, - d1 |
< z < 0, |
|
ïjк - |
|
|
|
|||||||
2ee0 |
|
|||||||||
ï |
|
|
|
|
|
|
|
(7.26) |
||
j(z) = í |
eN d |
|
|
|
2 |
|
|
|
||
ï |
|
(d 2 - z) |
, |
|
0 < z < d2 , |
|||||
ï |
ee |
0 |
|
|
|
|||||
î |
|
|
|
|
|
|
|
|
|
|
де φк – контактна різниця потенціалів. Формули (7.25 – 26) виведені з використанням наступних граничних умов: E(-d1) = E(d2) = 0 та φ(-d1) = φк, φ(d2) = 0. Хід залежності потенціалу в області просторового заряду p-n-переходу схематично показаний на рис. 7.7.
З (7.25) видно, що напруженість електричного поля максимальна на площині металургійного p – n-переходу (z = 0), лінійно спадає у області просторового заряду і дорівнює нулю на її межах z = - d1 та z = - d2. Максимальна величина напруженості
Рис. 7.7. Розподіл потенціалу вздовж p – n-переходу
|
|
|
Emax |
= |
eN a d1 |
= |
eN d d 2 |
, |
|
|
|
|
(7.27) |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
ee0 |
|
|
|
|
ee0 |
|
|
|
|
|
|
|||
з чого випливає співвідношення між |
протяжністю областей |
|||||||||||||||||||
збіднення у напівпровідниках n- та p-типу: |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
d2 = |
N a |
d1 . |
|
|
|
(7.28) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
N d |
|
|
|
|
|
|
|
|
|
|
|
З умови нерозривності потенціалу(7.26) |
на поверхні |
|||||||||||||||||||
металургійного p – n-переходу (z = 0) одержуємо |
|
|
|
|||||||||||||||||
Dy |
|
= |
e |
(N |
d 2 + N |
|
|
d 2 ) = |
e |
|
N 2 d 2 |
( |
1 |
+ |
1 |
) , |
||||
|
2ee0 |
|
|
2ee0 |
N a |
|
||||||||||||||
|
s0 |
|
|
a 1 |
d |
2 |
|
a 1 |
|
|
N d |
|||||||||
звідки знаходимо вирази для ширини збіднених областей з обох боків металургійногоp – n-переходу
d1 |
= |
2ee0 Dy s0 |
N d |
, |
d2 |
= |
2ee0Dy s0 |
N a |
, |
(7.29) |
||
e |
N a (N a + N d ) |
e |
N d (N a + N d ) |
|||||||||
|
|
|
|
|
|
|
||||||
тобто при істотних |
різницях |
концентрації |
|
домішок різного типу |
|
ширина облас |
||||||
просторового заряду буде різною – більшою там, де концентрація менша; p – n-перехід у цьому випадку називається несиметричним. Зокрема, повна ширина області просторового заряду
d = d1 + d2 |
= |
2ee0 Dy s0 |
N a + N d |
= |
2ee0Dy s0 |
p p + nn |
(7.30) |
|
e |
N a N d |
e |
p p nn |
|||||
|
|
|
|
при Na >> Nd буде майже рівною d2 – область збіднення практично повністю знаходиться у напівпровіднику n-типу.
Наявність потенціального бар’єру для основних носіїв заряду уp – n-переході надає йому властивостей, характерних для розглянутого вище бар’єра Шотткі. Зокрема, він також володіє односторонньою провідністю, що дає можливість створювати на його основі напівпровідникові діоди. Детальніше це питання буде розглянуте у розділі 9.
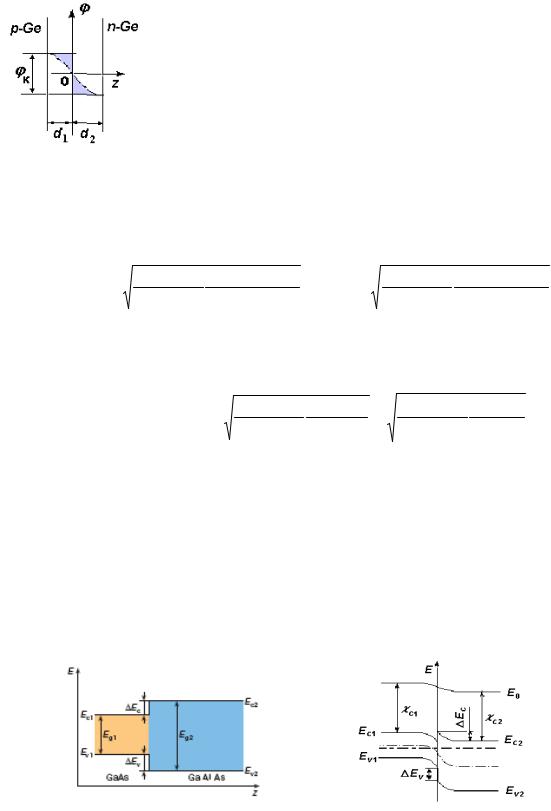
7.6. Гетеропереходи та низьковимірні структури
Ще одним типом бар’єрних структур є гетероперехід – контакт двох різних за своєю природою напівпровідників з різною шириною забороненої (рисзони. 7.8 а). Гетеропереходи характеризуються рядом специфічних особливостей, що дають
а) |
б) |
Рис. 7.8. Зонна діаграма гетеропереходуp-GaAs – n-Ga1-xAlxAs (твердий розчин алюмінію в арсеніді галію змінного складу (0 < x < 1) а) до та б) після встановлення рівноваги
