
FTT-stud / view6
.pdfРОЗДІЛ 6. ОПТИЧНІ ЯВИЩА В НАПІВПРОВІДНИКАХ
6.1. Механізми поглинання світла у кристалах
Відомо, що речовина, поміщена у зовнішнє електромагнітне ,полездатна поляризуватися та намагнічуватися. Явища поляризації та намагнічування речовини пояснюються дією сил поля, що змінюють характер руху електронів і ядер, які входять до складу її молекул. Ступінь поляризації і намагнічування речовини залежить від її властивостей та силових характеристик електричної і магнітної складових зовнішнього електромагнітного поля.
Енергія електромагнітної хвилі, падаючої на поверхню речовини, розподіляється у точці падіння між відбитою і заломленою хвилями. Емпіричним шляхом встановлено, що інтенсивність заломленої хвилі зменшується тим сильніше, чим довший шлях вона пройшла у речовині. Явище зменшення інтенсивності електромагнітної хвилі при проходженні її через речовину називаєтьсязгасанням і пояснюється різними процесами взаємодії хвилі з речовиною. Причиною згасання електромагнітної хвилі у однорідному середовищі є процеси поглинання, а в неоднорідному, крім того, – розсіювання.
Поглинанням називається явище зменшення інтенсивності електромагнітної хвилі при проходженні її через речовину внаслідок перетворення енергії поля у внутрішню енергію речовини або у енергію вторинного випромінювання, що має інший спектральний склад та інші напрямки поширення. Внаслідок поглинання може відбуватися нагрівання речовини, іонізація атомів або молекул, фотохімічні реакції, фотолюмінісценція і т.п.
Кількісною мірою ефективності процесу поглинання |
речовиноюлінійнийє |
||||
коефіцієнт поглинання – скалярна фізична величина |
|
||||
a = |
1 |
|
dI |
, |
(6.1) |
|
|
||||
|
I dx |
|
|||
яка має зміст відносної швидкості зміни інтенсивності хвиліІ при зміні довжиних пройденого нею шляху у речовині. Згідно експериментально встановленогозакону Бугера-Ламберта зміна інтенсивності монохроматичного світла при зміні глибини його проникнення у речовину визначається експоненціальною залежністю
I (x) = I0e-ax , |
(6.2) |
де І0 = І(0). Коефіцієнт поглинання є характеристикою поглинаючої системи ,і як видно з означення, вимірюється у одиницях, обернених до одиниць вимірювання довжини. У оптичній спектроскопії кристалів зручною одиницею вимірювання α є см-1.
Розсіюванням називається процес перетворення енергії електромагнітної хвилі у неоднорідному середовищі, яке супроводжується зміною напрямку її поширення і проявляється у вигляді невластивого світіння речовини. Невластиве світіння обумовлене вимушеними коливаннями електронів у атомах розсіюючого середовища, викликаними дією періодично змінного поля електромагнітної хвилі.
Кількісною мірою ефективності процесу розсіювання є коефіцієнт екстинції ε – скалярна фізична величина, що визначається подібно до(6.1) і має аналогічний зміст– відносної швидкості зміни інтенсивності при зміні довжини пройденого хвилею шляху у речовині. Різниця між коефіцієнтами поглинання і екстинції полягає у тому, що вони характеризують швидкість згасання хвилі внаслідок різних причин– поглинання або розсіювання, відповідно. Якщо у середовищі обидва процеси протікають одночасно, то зміна інтенсивності монохроматичної хвилі при заглибленні її у речовину визначається залежністю
I (x) = I0e-(a+e ) x . |
(6.3) |
Причиною поглинання світла речовиною є взаємодія електромагнітної хвилі з зарядженими частинками, що входять до складу речовини(електронами, ядрами атомів, іонами). З боку електромагнітного поля хвилі на частинки діють сили , що змінюють

характер їх руху – переводять у збуджений стан. Внаслідок трансляційної симетрії ґратки збудження не може бути локалізованим, а тому пошириться на увесь кристал у вигляді хвилі, яка переносить енергію. Отже має місце перетворення енергії зовнішнього електромагнітного поля у енергію збудження. При цьому енергія збуджуючої електромагнітної хвилі зменшується і тим більше, чим довший шлях вона проходить у речовині, що й трактується як поглинання.
Залежно від типу збудження, викликаного електромагнітною хвилею у кристалі, поглинання світла у ньому може здійснюватись за одним з наступних механізмів:
-фундаментального (властивого) поглинання;
-екситонного поглинання;
-поглинання вільними носіями зарядів;
-домішкового поглинання;
-поглинання кристалічною ґраткою.
6.2. Фундаментальне поглинання
Якщо на напівпровідниковий кристал падає світло частотиν з видимого діапазону, то енергії фотона може вистачити для того, щоби перевести електрон з валентної зони у зону провідності. Такі переходи супроводжуються поглинанням світла, яке назване властивим, оскільки вони викликають появу провідності, властивого для напівпровідників типу, при якому носіями струму є різнойменно заряджені квазічастинки– електрони та дірки (це явище називається внутрішнім фотоефектом). Оскільки для реалізації властивого поглинання необхідно виконання умови hν ≥ Eg, то це обумовлює наявність червоної межі внутрішнього фотоефекту – максимальної довжини хвилі λmax = hc/Eg, яка може викликати властиве поглинання. Значення її залежить від ширини забороненої зони напівпровідника і відповідає у різних кристалах видимому або ультрафіолетовому діапазону. Наприклад,
для Si (Eg ≈ 1,1eB) λmax ≈ 11300Å.
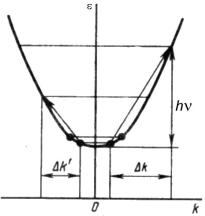
Розрізняють два типи процесів, що сприяють властивому поглинанню: прямі міжзонні переходи, що відбуваються без зміни квазіімпульсу електрона (на рис. 6.1 вони показані стрілками 1 і 3), та непрямі – зі зміною.
Реалізацію прямого переходу можна уявити наслідок зіткнення двох квазічастинок– електрона і фотона. Їх взаємодія відбуваються з виконанням законів збереження енергії та імпульсу
|
|
|
r |
|
r |
¢ |
r |
|
r |
r |
¢ |
, |
|
|
|
|
|
|
|
|
|
|
|
e(k ) + hn = e(k ) , |
p + pфот = p |
|
|
|
|
|
|
|
|
|
|
||||||||
r |
r |
|
r |
r¢ |
r¢ |
|
r |
¢ |
) – енергія і квазіімпульс |
|
|
|
|
|
|||||||
де e(k ) |
і p = hk (e(k ) і |
p |
= hk |
|
|
|
|
|
|
||||||||||||
електрона |
у |
початковому(кінцевому) |
енергетичному |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
станах з відповідним значеннями хвильового вектораk ; |
|
|
|
|
|
||||||||||||||||
r |
r |
– квазіімпульс фотона з хвильовим вектором |
|
|
|
|
|
||||||||||||||
pфот = hk |
|
|
|
|
|
||||||||||||||||
kr , що викликав такий перехід. У межах зони Бріллюена |
|
|
|
|
|
||||||||||||||||
k ≤ π/a, отже р ~ ћπ/a, тому при a = 3∙10-10 |
м квазіімпульс |
|
|
|
|
|
|||||||||||||||
електрона |
можна |
оцінити |
|
|
величиною |
|
|
10 |
ћ. |
Рис. 6.1. Дисперсійні криві |
|||||||||||
|
|
|
порядка10 |
|
|||||||||||||||||
Квазіімпульс фотона рфот = ћκ = 2πћ/λ з видимої області |
схема |
міжзонних |
|
переходів у |
|||||||||||||||||
спектра |
(λ |
~ |
5∙10-7 |
м) |
набуває значень близько108ћ. |
прямозонному напівпровіднику |
|||||||||||||||
Оскільки значення квазіімпульсу електрона набагато більше, |
ніж у фотона, |
то при їх |
|||||||||||||||||||
зіткненні він |
практично |
не |
змінюється. Тобто |
r |
r |
|
r |
|
r |
а тому й |
r |
r |
|||||||||
p¢ = |
p + pфот » |
p , |
k ¢ » k – це |
||||||||||||||||||
прямі переходи без зміни хвильового вектора; їх називають ще вертикальними. Теоретичний розрахунок коефіцієнта поглинання для прямих міжзонних переходів у
прямозонних напівпровідниках (таких, у структурі зонного спектра яких екстремуми
дисперсійних кривих валентної зони і зони провідності, як показано на рис. 6.1,
r
знаходяться у одній точці k -простору), дає наступний вираз:

|
e2 (2m)3 / 2 |
f |
hn - Eg , |
|
|
||
|
a = 4p nch2e |
0 |
m |
|
(6.4) |
||
|
|
0 |
|
|
|
|
|
де f – сила осцилятора |
переходу(безрозмірна |
величина, що |
визначає |
ймовірність |
|||
переходу), μ = me*mh*/(me* |
+ mh*) – приведена |
маса електрона |
й дірки, me* |
і mh* – їх |
|||
ефективні маси, а m0 – маса вільного електрона. |
|
|
|
|
|||
Хвильовий вектор квазічастинки є характеристикою її стану, |
тому хвильова функція |
||||||
|
|
|
|
|
|
|
r |
електрона у кристалі залежить не тільки від змінних – координат і часу, але й від k . За
r
теоремою Блоха, вона повинна мати вигляд(3.39), де ukr (r ) – періодична функція
координат з періодом ґратки. Поблизу вузлів кристалічної ґратки вона повинна описувати стан валентного електрона атома, локалізованого у цьому вузлі. Отже, функція Блоха (3.39) являє собою плоску хвилю, модульовану атомоподібними функціями (типу s- або p- орбіталей).
У центрі зони Бріллюена координатна |
r r |
повністю |
частина функції Блохаu (r ) |
||
|
k |
|
збігається з атомоподібною, тому для переходів |
типу1 (рис. 6.1) повинні виконуватись |
|
правила відбору, встановлені для ізольованих атомів. В електродипольному наближенні таке правило має вигляд l = ± 1 (l – орбітальне квантове число). Тому, якщо, наприклад, верхні стани валентної зони прямозонного напівпровідника відповідають s-, а нижні стани
зони |
провідності – p-оболонкам |
ізольованого |
|
атома, то |
вказані |
переходи |
будуть |
|||||||||||
дозволеними. |
Якщо ж стани зони провідності походять від одноелектронних d-станів |
|||||||||||||||||
атома, то переходи будуть забороненими. Проте у інших точках зони Бріллюена така |
||||||||||||||||||
заборона не діє – у цьому випадку можуть здійснюватись |
прямі переходи типу 3. |
|||||||||||||||||
Коефіцієнт поглинання “заборонених” переходів визначається формулою |
|
|||||||||||||||||
|
|
|
|
|
|
|
e2 (2m)5/ 2 |
|
¢ |
|
(hn - Eg )3/ 2 |
|
|
|
||||
|
|
|
|
|
a = |
3p nch2e0 m02 × f |
× |
|
hn |
. |
|
(6.5) |
||||||
|
|
|
|
|
|
|
|
|||||||||||
Вважаючи, що me* = mh* = m0, n = 4 і f′ = f = 1, одержуємо |
для “дозволених” |
|||||||||||||||||
вертикальних переходів α = 6,7∙104∙(hν – Eg)1/2 см-1, а для “заборонених” – α′ ≈ 4,5∙104∙(hν – |
||||||||||||||||||
Eg)3/2/hν см-1. Зокрема, при hν ~ 1 еВ на краю властивого поглинання, де hν – Eg ~ 0,01 еВ, |
||||||||||||||||||
коефіцієнт |
поглинання |
напівпровідника |
досягає |
величини104 – 105∙см-1 у випадку |
||||||||||||||
дозволених переходів, що значно переважає його значення, характерні будь-якому іншому |
||||||||||||||||||
механізмові |
поглинання. |
З |
цієї |
причини |
|
властиве |
поглинання часто |
називають |
||||||||||
фундаментальним. Коефіцієнт поглинання для “заборонених” переходів при тих самих |
||||||||||||||||||
значеннях параметрів сягає 100 см-1. |
|
|
|
|
|
|
r |
|
|
|
|
|||||||
Якщо дно зони провідностіEc |
|
|
|
|
|
|
|
|
|
|
||||||||
відповідає значенню k іншому, ніж верх валентної |
||||||||||||||||||
зони Ev (рис. 6.2), як це має місце у випадку Si, Ge та |
|
|
|
|
|
|||||||||||||
багатьох напівпровідникових сполук, то відстань Egо |
|
|
|
|
|
|||||||||||||
по вертикалі між зонами більша, аніж ширина |
|
|
|
|
|
|||||||||||||
забороненої зони Eg. Тоді |
прямі оптичні |
переходи |
|
|
|
|
|
|||||||||||
(типу |
1) |
можуть |
збуджуватись |
тільки |
квантами |
|
|
|
|
|||||||||
світла з енергіями hn ³ Egо. Величину Egо називають |
|
|
|
|
|
|||||||||||||
оптичною |
|
|
шириною забороненої |
|
|
|
|
|
|
|
|
|
|
|||||
напівпровідника. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Непрямі |
міжзонні |
переходи |
відбуваються |
зі |
|
|
|
|
||||||||||
зміною |
|
|
|
|
|
|
|
|
r |
|
r |
|
|
|
|
|
||
квазіімпульсу електрона, тобто при k ¢ ¹ k . |
|
|
|
|
|
|||||||||||||
Оскільки зміна імпульсу електрона при поглинанні |
|
|
|
|
||||||||||||||
одного фотона неможлива, а одночасне зіткнення з |
Рис. 6.2. Дисперсійні криві і схем |
|||||||||||||||||
більшою |
їх |
кількістю малоймовірне, то непрямі |
||||||||||||||||
переходи здійснюються внаслідок процесів тільки за |
міжзонних переходів у непрямозон- |
|||||||||||||||||
участі “третіх |
тіл” |
– частинок |
іншої природи, ніж |
ному напівпровіднику |
|
|||||||||||||
|
|
|
|
|
||||||||||||||
фотон і електрон. У якості таких найімовірніше можуть виступати збудження коливань атомів кристалічної ґратки – фонони.
Поглинання світла у процесах міжзонних переходів із зміною квазіімпульсу супроводжується зникненням фотона і фонона, сумарна енергія яких витрачається на перевід електрона з валентної зони у зону провідності. Тоді поглинання стає можливим і
поза смугою фундаментального поглинання, тобто за умови hν < Eg.
При hν > Eg поглинання може супроводжуватися також і народженням фонона – надлишкова енергія фотона передається ґратці. У обох випадках закони збереження набувають вигляду
r |
r¢ |
r r |
r |
r |
¢ |
, |
e(k ) + hn ± hw = e(k ) , |
p + pфот ± pфон = p |
|
||||
звідки, зокрема, випливає необхідність зміни хвильового вектора електрона:
r r |
r |
r |
r |
r |
k ¢ = k +k |
± q |
» k ± q |
||
(знак плюс відповідає процесам з поглинанням, а мінус – з випромінюванням фонона з
частотою w, імпульсом |
r |
r |
pфон |
і хвильовим вектором q ). Такі переходи показані стрілками |
2 на рис. 6.1 і 6.2.
В області малих енергій фотона(hν < Eg – ħω) коефіцієнт поглинання дорівнює нулю; на краю смуги фундаментального поглинання, де Eg – ħω ≤ hν < Eg, – можливі непрямі переходи з поглинанням фонона для яких
aпог = |
|
A (hn - Eg |
+ hw)2 |
|
||||
|
|
|
|
|
, |
|
(6.6) |
|
|
|
|
|
|
||||
|
|
exp(hw / k БT ) -1 |
|
|||||
а при hν > Eg + ħω – з випромінюванням, де |
|
|
|
|
||||
aвип |
= |
A(hn - Eg - hw)2 |
|
(6.7) |
||||
|
- exp(-hw / kБT ) |
|||||||
|
1 |
|
||||||
(тут А – слабко залежна від частоти |
світлаν |
функція). На |
відрізку Eg ≤ hν ≤ Eg + ħω |
|||||
можливі процеси як з поглинанням, так і з випромінюванням фононів, отже тут α = αпог +
αвип.
Оскільки ймовірність протікання процесів з участю трьох частинок значно менша, ніж процесів з участю двох – електрон і фотон, то коефіцієнт поглинання в області непрямих міжзонних переходів набагато менший, ніж в області прямих переходів.
Значення його істотно залежить від температури– при охолодженні напівпровідника процеси з поглинанням фонона протікають рідше і коефіцієнт поглинання за схемою непрямих переходів зменшується.
Положення краю фундаментального поглинання у напівпровідниках визначається шириною забороненої зони, яка, у свою чергу, залежить від структури енергетичних зон, а вона змінюється під дією зовнішніх чинників. Наприклад, при стискуванні кристалу змінюється постійна ґратки, а з нею й структура енергетичного спектру. При всебічному стискуванні кристала Eg може як зменшуватись, так і збільшуватись. Це означає можливість зсуву краю фундаментального поглинання у довгоабо короткохвильову область спектра. Цей самий ефект може досягатись зміною температури напівпровідника. Зсув краю фундаментального поглинання у довгохвильову область спектра можливий також внаслідок дії зовнішнього електричного поля (ефект Франца-Келдиша), яке змінює енергію вільних носіїв і зонну структуру в цілому. Останнє проявляється у появі можливості переводу електрона у зону провідності шляхом збудження його фотонами, енергія яких дещо менша значення Eg, визначеного за відсутності електричного поля.
6.3. Екситонне поглинання
Відповідно з викладеними вище міркуваннями, переходи електронів з валентної зони у зону провідності внаслідок поглинання світла можливі тільки тоді, коли енергія фотонів

hν не менша ширині забороненої зониEg. Проте експериментальні дослідження поглинання світла в області фундаментального поглинання закису міді(Cu2O) показали, що кристал здатний поглинати кванти і з енергією, дещо меншою, ніж ширина забороненої зони, до того ж без появи електропровідності.
Пояснення цього явища полягає у припущенні можливості взаємодії збудженого світлом електрона з діркою, що утворилася у валентній зоні. В результаті цієї взаємодії електрон і дірка знаходяться у зв’язаному стані. При цьому вони здатні рухатись, обертаючись навколо спільного центра мас, який може поступально рухатися по кристалу.
Віддаль між електроном і діркою (радіус екситона) становить декілька періодів ґратки кристалу. З цієї причини пара зв’язаних частинок(електрон і дірка) названа екситоном великого радіуса або екситоном Ваньє-Мотта.
У діелектриках і напівпровідниках з великою діелектричною проникністю основні особливості такого збудження описуються на основі найпростішої енергетичної моделі, де електрон і дірка розглядаються як квазічастинки з однаковими по величині зарядами протилежного знаку, що взаємодіють між собою з силою кулонівської взаємодії. У
найпростішому випадку параболічних |
зон з екстремумом в центрі зони Бріллюена |
||||||||||||
залежність енергії електрона провідності та дірки з валентної зони від хвильового вектора |
|||||||||||||
можна подати у вигляді |
2 |
|
2 |
|
|
|
2 |
|
2 |
|
|
||
r |
k |
|
r |
k |
|
|
|||||||
ec (k ) = |
h |
|
|
, |
ev (k ) = - |
h |
|
|
- Eg , |
(6.8) |
|||
2me* |
2mh* |
||||||||||||
|
|
|
|
|
|||||||||
а рівняння Шредінґера системи взаємодіючих частинок електрон-дірка –
|
h |
2 r |
|
h2 r |
|
e2 |
1 |
|
|
r r |
|
||||||
[- |
|
|
Ñ2 |
- |
|
Ñ2 |
- |
|
|
|
r |
r |
- E |
g |
]Y(r |
, r |
) = EY |
|
|
|
|
|
|||||||||||||
|
2me* |
e |
|
2mh* |
h |
|
4pee0 |
|
re - rh |
|
e |
h |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
|
|
|
де E – енергія системи у стаціонарному стані Y(re , rh ) . |
|
|
|
|
|||||||||||||
r r
Для подальшого розгляду зручніше перейти від координатre , rh до нових змінних:
r r
(re , rh ) , (6.9)
електрона і дірки
|
r |
m*rr + m*rr |
|||
- |
R = |
e |
e |
h h |
– радіус-вектор центра мас екситона при спільному (переносному) |
|
mex |
|
|||
|
|
|
|
|
|
рухові електрона й дірки; |
|||||
- |
r |
r |
r |
– координати їх відносного руху. Оскільки вказані рухи можуть |
|
r = rh |
- re |
||||
здійснюватись незалежно один від одного, то введенням двох нових хвильових функцій
r |
r |
y (R) |
і j(r ) , кожна з яких описує один з цих рухів, рівняння Шредінґера зводиться до |
пари незалежних рівнянь, що описують рух пари в цілому, та їх відносний рух. Дійсно,
r r |
r r |
r |
r |
поклавши у (6.9) Y(re , rh ) = Y(R, r ) = y (R)j(r ) , запишемо його у вигляді системи |
|||
ì |
|
|
|
h |
2 |
r |
|
r |
r |
|
|
ï |
|
[- |
|
|
Ñ2r |
]y (R) = E ry (R) |
|
||||
|
* |
* |
|
||||||||
ï |
|
|
|
|
R |
|
|
R |
(6.10) |
||
í |
|
h2 |
2(me |
+ mh ) |
|
|
|
|
, |
||
ï |
|
r 2 |
e2 |
|
|
r |
|
r |
|
||
ï[- |
|
Ñrr - |
|
|
]j |
(r ) |
= |
(Err + Eg )j(r ) |
|
||
|
|
|
|
||||||||
î |
|
2m |
|
4pee0 r |
|
|
|
|
|||
де μ = m*em*h /(m*e + m*h) – приведена |
|
маса |
електрона і дірки, а ER та Er – енергії |
||||||||
переносного та відносного рухів цієї пари частинок. |
|
||||||||||
Розв'язком першого рівняння системи(6.10) є хвильова функція вільної частинки |
|||||||||||
масою mex = m*e + m*h, |
що |
рухається |
|
у |
кристалі. Внаслідок трансляційної |
симетрії |
|||||
кристалу, вона повинна володіти хвильовими властивостями. Подібно до інших вільних частинок у кристалі – електрона провідності, дірки, – її функція стану може бути подана у вигляді плоскої хвилі

r r r
y (R,t) = Aei[( K ,R)-wt ] ,
r
з хвильовим вектором K . Енергія, яку переносить ця хвиля – енергія поступального руху екситона
r |
2 |
K |
2 |
|
|
|
ER (K ) = |
h |
|
|
. |
(6.11) |
|
|
|
|
|
|||
|
2mex |
|
||||
Друге рівняння системи (6.10) подібне до рівняння Шредінґера для електрона у атомі водню. Тому його розв’язок – енергію і функцію стану екситона, можна подати у вигляді, подібному до енергії і функції стану електрона у атомі водню, з умовою заміни маси електрона на приведену масу екситонаμ та його заряду на величинуe/ε. Тоді енергія зв’язаного стану екситона знаходиться за формулою, подібною до формули, що визначає енергію зв’язку електрона у атомі водню:
Ern = - |
Rex |
, |
(6.12) |
|
|||
|
n2 |
|
|
r
а хвильова функція стану з енергією(6.11) jn (r ) може бути знайдена з відповідної
хвильової функції електрона в атомі водню заміною його маси на ефективну масу електрона у кристалі, а постійної Рідберґа– на величину Rex = μe4/ (2ћ2ε2) – постійна Рідберґа екситона (енергія зв'язку електрона і дірки в екситоні); n = 1, 2, … - квантове число. Зокрема, в основному стані екситона n = 1
|
|
|
|
|
|
r |
1 |
|
- |
r |
|
|
|
|
|
|
j |
|
e |
aex , |
(6.13) |
||||
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
(r ) = |
2p aex |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
де |
aex = |
h |
2e |
– екситонний радіус Бора. |
|
|
|
|
|
|
||
m e2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
Повна енергія екситона є сумою(6.11) і (6.12); значення її при кожному значенні хвильового вектора квантуються, так що
r |
2 |
K |
2 |
|
Rex |
|
|
|
En (k ) = |
h |
|
|
- |
, |
(6.14) |
||
2mex |
|
|||||||
|
|
n2 |
|
|||||
а нормована на об’єм кристалу Ω хвильова функція цього стану –
r r |
1 |
r |
r r |
|
|
i[( K ,R)-wt ] |
. |
(6.15) |
|||
YnKr (r , R, t) = |
W |
jn (r )e |
|
||
|
|
|
|
|
При K = 0 перший доданок у (6.14) відсутній – є тільки відносний рух електрона і дірки, тоді як центр їх мас нерухомий. Це означає, що екситон Ваньє-Мотта можна уявити як пару „електрон-дірка”, що обертається навколо спільного центра мас. Другий доданок відповідає дискретним (n = 1, 2, 3, ...) збудженим станам водневоподібного атома з
приведеною масою μ, який знаходиться в однорідному середовищі з діелектричною
r
проникністю ε. Оскільки хвильовий вектор K може набувати довільного зN значень у першій зоні Бріллюена (N – кількість атомів у кристалі), то кожному дискретному рівню n такого „атома” у кристалі відповідає енергетична зона певної ширини.
Окрім енергії, характеристикою екситонного стану є такожрадіус екситона – величина, що вводиться аналогічно до радіуса орбіти електрона у n-му стані атома водню:
r = a |
ex |
× n2 . |
(6.16) |
n |
|
|
Відзначимо, що екситонні розміри можуть бути досить значними. Наприклад, у випадку класичного напівпровідника германію аех = 80аВ (аВ = 0,529 Å – борівський радіус атома водню), що значно перевищує розміри атома германію і постійну його ґратки
а = 5,657 Å.
Оскільки енергія зв’язаного стану електрона менша, аніж у вільного (у межах зони провідності), то енергетичні рівні екситона, що визначаються формулою(6.12), знаходяться під дном зони провідності. Як показали експериментальні дослідження, глибина залягання їх у забороненій зоні становить близько0,01 еВ. Переходи між цими рівнями супроводжуються поглинанням та випромінюванням енергії, що формує відповідний оптичний спектр. Очевидно, він має бути подібним до атомних спектрів– лінійчатим, з виконанням серіальних закономірностей. При цьому спектральні лінії екситонних серій зміщені відносно ліній водневоподібних атомів у бік ІЧ-діапазону, оскільки стала Рідберґа системи зв’язаних електрона й діркиRеx значно менша її значення для атомів.
Збудження екситонів – перехід електронів з валентної зони екситонні стани, – супроводжується поглинанням світла. Саме цей процес називаютьекситонним поглинанням. Спостережуваний спектр екситонного поглинання має вигляд вузьких ізольованих смуг (а не ліній) на краю області фундаментального поглинання. Розширення спектральних ліній у смуги свідчить про можливість трансляційного руху екситона у кристалі.
Вперше експериментально екситонну спектральну серію було зареєстровано на краю смуги фундаментального поглинання кристалів закису міді, де було зареєстровано дві водневоподібні серії:
En = (2,173 - 0,0968/n2) eВ |
(n = 2, 3, 4, 5, 6), |
та |
|
En = (2,306 - 0,154/n2) eВ |
(n = 2, 3, 4). |
Існування двох серій зумовлене екситонними станами, що утворюються двома валентними зонами та однією зоною провідності напівпровідника.
Водневоподібний спектр екситнів був спостережуваний експериментально також у інших кристалах. Зокрема, у кристалі дийодиду свинцюPbI2 чотири інтенсивні лінії спектра екситонного поглинання описуються формулою
En = (2,568 - 0,142/n2) eВ (n = 2, 3, 4, 5).
6.4. Поглинання світла вільними носіями
За наявності вільних носіїв заряду у кристалах на частотах ІЧ-діапазону, недостатньо високих для реалізації міжзонних переходів або збудження екситонних станів, поглинання електромагнітних хвиль може здійснюватися за рахунок переходів між одноелектронними станами у межах однієї зони дозволених значень енергії. Вони відбуваються тільки всередині незаповнених зон, що завжди має місце у кристалічних провідниках – металах, а також у напівпровідниках за наявності електронів у зоні провідності та( бо) дірок – у валентній. Оскільки при таких переходах змінюється хвильовий вектор носія (рис. 6.3), то вони можуть відбуватися тільки за участі “третіх тіл”.
З класичної точки зору поглинання вільними носіями відбувається таким чином: електрони (дірки) прискорюються електричним полем світлової
хвилі |
, і розсіюючись |
на |
спотвореннях |
ґратки |
||||
(коливаннях |
атомів, |
домішках, |
вакансіях |
і |
т.),.п |
|||
частково передають їм свою енергію. Іншими словами, |
||||||||
енергія |
падаючої |
електромагнітної |
хвилі(світла) |
|||||
витрачається на збільшення енергії теплового руху у ґратці (збудження фононних станів). Класична теорія встановлює для такого механізму залежність коефіцієнта поглинання вільними носіями від довжини хвилі у вигляді
Рис. 6.3. Схема переходів між рівнями зони провідності

a = |
e3 |
× |
ncl2 |
, |
(6.17) |
|
4pe0c3 |
nmm* |
|||||
|
|
|
|
де n – показник заломлення кристалу, nc – концентрація носіїв, μ – їх рухливість, а m* – ефективна маса.
За відсутності виродження зон для поглинання у ІЧ-області квантова теорія дає практично той самий результат – α ~ λ2, що підтверджується експериментально. Проте у
ближній ІЧ-області, а у ряді матеріалів і у видимій, при розсіянні на акустичних коливаннях α ~ λ1,5, на оптичних – α ~ λ2,5, на домішках – α ~ λ3-3,5. Тобто, залежність α від
λвизначається ще й природою “третіх тіл”.
Уреальних кристалах в деякій мірі присутні усі вказані типи розсіяння, тому залежність α від λ не визначається простим степеневим законом; однак завжди із збільшенням довжини хвилі поглинання швидко зростає. З (6.17) видно, що величина
коефіцієнта поглинання пропорційна концентрації носіївnc. У досконалих напівпровідниках за умови низьких температур і відсутності освітленняnc » 0, у домішкових – визначається концентрацією домішкових атомів, а у металах – близька до кількості атомів ґратки (~ 1026 м-3). Отже, у діапазоні великих довжин хвиль (ІЧ-область) напівпровідники поглинають тільки за наявності провідності(зазвичай домішкової), а метали – завжди і значно сильніше. При зменшенні λ до видимого та УФ-діапазону метали майже не поглинають, відбиваючи практично повністю; в УФ-області вони прозорі.
Зокрема, характерний блиск металевих поверхонь пояснюється саме ефективним відбиванням падаючого світла.
6.5. Домішкове поглинання
Явище поглинання світла за участі локальних рівнів із забороненої зони називається домішковим. Причина домішкового поглинання пов’язується з переходами типу „зона – рівень”, „рівень – зона” або „рівень – рівень” (рис. 6.4). Вони можливі за умови, що енергії поглиненого фотона достатньо для переводу електрона з початкового стану у кінцевий, а вигляд спектра поглинання істотно залежить від конкретного типу переходу.
Якщо Еак |
– енергія |
активації локального |
рівня |
|
|
|||
(робота, яку необхідно для переведення електрона |
|
|
||||||
заселеного рівня до зони провідності(перехід 1 на рис. |
|
|
||||||
6.4) або дірки з валентної зони – на незаповнений рівень |
|
|
||||||
(перехід 2) у |
забороненій |
зоні), то |
при |
опроміненні |
|
|
||
напівпровідника |
електромагнітним |
полем, |
енергія |
|
|
|||
квантів якого hν ≥ Eак, одержується неперервна |
смуга |
|
|
|||||
домішкового поглинання. |
|
|
|
|
|
|
|
|
У випадку збудження донорних та акцепторних |
|
|
||||||
рівнів, глибина |
залягання |
якихЕак ~ 0,01 |
еВ, |
|
смуга |
|
|
|
поглинання лежить у далекій ІЧ-області спектра. На |
|
|
||||||
відміну від фундаментального, поглинання цього типу |
|
|
||||||
супроводжуються виникненням вільних носіїв тільки |
|
|
||||||
одного знаку – електронів |
або дірок |
і спостерігається |
|
|
||||
при низьких температурах, коли |
основна |
|
частина Рис. |
6.4. Схема |
перходів з |
|||
домішкових атомів ще не іонізована. |
|
|
|
участі |
локальних |
домішко |
||
Можливі також переходи електронів |
з |
|
станів |
|
|
|||
валентної |
|
|
||||||
зони на звільнені внаслідок термічної активації донорні рівні або з заповнених з тієї ж причини акцепторних рівнів– у зону провідності. Такі переходи супроводжуються поглинанням на довгохвильовій межі фундаментального поглинання і появою домішкової провідності. Спектр поглинання цього типу має вигляд смуги, що накладається на смугу поглинання, викликаного вільними носіями та екситонні лінії. Коефіцієнт поглинання за таким механізмом залежить від частоти електромагнітного поля за законом

a = A × N d hn - Eg + Eак , |
(6.18) |
де Nd – концентрація домішкових атомів, А – константа, значення якої залежить від типу напівпровідника і домішки. Характерні значення А ~ 10-18, якщо концентрація вимірюється у см–3, енергія – у еВ, а коефіцієнт поглинання – у см-1. З цього випливає, що
при середніх концентраціях домішкових атомів~ 10 |
16 |
-3 |
|
см коефіцієнт поглинання |
становить величину 1 – 10 см-1.
Деякі атоми, наприклад елементи III і V груп у Si та Ge, утворюють у забороненій зоні напівпровідника декілька рівнів. У цьому випадку освітлення кристалу приводить до збудження електронів домішки, тобто їх переходу з основного стану у збуджений, обидва з яких знаходяться у забороненій зоні напівпровідника. Такі переходи (показані стрілкою 3 на рис. 6.4) супроводжуються поглинанням світла у видимій області, але без зміни провідності кристалу (їх називають внутрішньоцентровими). Спектр внутрішньоцентрових переходів має лінійчатий вигляд.
Зрозуміло, що коефіцієнт домішкового поглинання за довільною з можливих схем істотно залежить від концентрації домішкових атомів, проте завжди αдом << αфунд.
6.6. Поглинання кристалічною ґраткою |
|
||||
До сих пір явище поглинання світла |
пов’язувалося з можливістю збуренн |
||||
електронної системи кристалу зовнішнім електромагнітним полем. Проте, воно може |
|||||
змінювати також і стан фононної системи, отже за рахунок енергії поглиненого фотона у |
|||||
кристалі можуть виникати додаткові фонони. |
|
||||
Якщо кристал з іонним типом |
зв’язку знаходиться у зовнішньому електричному |
||||
полі, то різнойменно заряджені іони змістяться |
під дією сил поля у протилежних |
||||
напрямках – виникне |
електричний |
дипольний |
момент. Тоді падаюча на кристал |
||
електромагнітна |
хвиля |
змусить |
іони |
ґратки коливатися з частотою зміни зовнішнього |
|
поля. Робота, |
яку виконує |
поле |
для виникнення і підтримання таких коливань, |
||
здійснюється за рахунок енергії хвилі. |
Отже, електромагнітна хвиля втрачає енергію при |
||||
поширенні її у кристалі– поглинається системою змінних диполів. Внутрішня енергія кристалу при цьому зростає за рахунок збудження у ньому коливних станів– оптичних
фононів. |
|
|
Нехай у результаті елементарного акту поглинання світла |
ґраткою |
зникає фотон з |
r |
|
r |
енергією hν і хвильовим вектором k , а у кристалі виникає фонон у стані |
q . При цьому |
|
повинні виконуватися закони збереження енергіїhν = ћω та |
|
r r |
квазіімпульсу k = q . |
||
Внаслідок того, що для збудження коливного руху необхідно долати сили пружних взаємодій між атомами, значно менших, ніж сили взаємодій між електронами та ядрами, енергія фононів істотно менша від енергії збудження електронних станів за механізмом міжзонних переходів і складає величину близько 0,01 еВ. Тому значення фононних частот відповідають ІЧ-області спектра. Відповідно, значення хвильових векторів фотона, що поглинається, і фонона, що виникає при цьому, дуже малі. Оскільки енергія акустичного
r
фонона з q » 0 дуже мала, то це означає, що у результаті поглинання електромагнітної хвилі можуть збуджуватись тільки оптичні фонони. Сильне поглинання на частотах поперечних оптичних коливань зареєстроване у сполуках елементів III і V та II і VI груп з іонно-ковалентним типом зв’язку.
У ковалентних кристалах, таких як Si та Ge, поглинання, викликане збудженням коливань ґратки, також спостерігається, причому у досить широкій спектральній області, хоча і значно слабше, ніж в іонних. Воно пов’язане з тим, що електромагнітні хвилі здатні взаємодіяти також і з акустичними коливаннями, які спричиняють періодичні зміни розподілу густини заряду у кристалі, що супроводжується появою змінного електричного поля і, як наслідок, – поглинанням енергії хвиль. Із закону збереження імпульсу випливає можливість такого поглинання за участі не одного, а принаймні двох фононів: при kr » 0 з рівності
|
|
r r |
r |
|
r |
r |
k = q1 |
+ q2 |
|
. Закон збереження енергії у цьому випадку має вигляд |
||||
випливає q1 |
» -q2 |
|||
hn = hw1 + hw2 ,
де ω1 і ω2 – частоти фононів, що народжуються у результаті зникнення фотона. Взагалі кажучи, вони можуть належати різним гілкам закону дисперсії, наприклад, один – оптичній, а другий – акустичній.
У наведених схемах розглядаються тільки процеси поглинання світла, пов’язані з народженням фононів. Це має місце за умови низьких температур, коли відсутнє термічне збудження коливного руху. Проте при високих температурах рівноважні концентрації фононів великі, так що можливими стають процеси поглинання фотона і фонона
r |
r |
hn + hw1(q) = hw2 |
(-q) , |
енергія яких передається народженому фонону з близьким значенням хвильового вектора.
6.7. Фотопровідність
Освітлення |
напівпровідника |
у |
області |
фундаментального |
або |
домішковог |
|||
поглинання супроводжується появою нерівноважних вільних носіїв заряду. Вказане явище |
|
||||||||
називається |
внутрішнім фотоефектом, а виникнення при цьому додаткової(понад |
|
|||||||
теплову) електропровідності – фотопровідністю. |
|
|
|
|
|||||
Явище |
фотопровідності використовується для створення пристроїв реєстрації |
||||||||
світлового |
випромінювання – |
фотоприймачів, модуляторів світлових |
потоків |
та |
|||||
перетворювачів світлової енергії в електричну(сонячних батарей). Принцип дії цих |
|||||||||
пристроїв ґрунтується на можливості зміни опору напівпровідника при зміні освітленості |
|
||||||||
(з цієї причини їх називають також фоторезисторами). |
|
|
|
|
|||||
Будову |
світлочутливого |
елемента |
фоторезистора схематично можна |
уявити |
як |
||||
плівку, виготовлену з моноабо полікристалічного напівпровідника. За допомогою пари омічних контактів його підключають до джерела напругиU0. Товщина світлочутливого елемента повинна бути достатньо великою, щоби у ньому поглиналася практично уся енергія світла, що попало у кристал. Ця умова легко виконується у випадку фоторезисторів, які працюють в області властивого поглинання і значно складніше для домішкових. Якщо вона виконується, то кількість носіїв(у випадку властивого
поглинання – електрон-діркових пар), які генеруються за одиницю |
часу внаслідок |
||
освітлення поверхні фоторезистора при λ < λmax, становить величину |
|
||
g = |
W0 |
(1 - r)h . |
(6.19) |
|
|||
|
hn |
|
|
Тут W0 – потужність світла, що падає на поверхню фоторезистора з коефіцієнтом відбивання r; λmax – червона межа внутрішнього фотоефекту, а η – його квантовий вихід – середня кількість носіїв (електрон-діркових пар), утворених кожним поглиненим фотоном частоти ν. Якщо при поглинанні високоенергетичного фотона народжується декілька електрон-діркових пар, то η > 1; у випадку поглинання частини фотонів без появи вільних носіїв (наприклад внаслідок переходів між станами всередині однієї зони) – η < 1.
Припустимо, що при досить тривалому незмінному за інтенсивністю освітленні у кристалі об’єму Ω збуджено фотоелектрони з надлишковою(понад рівноважну n0) стаціонарною концентрацією n = gτ/Ω. Після припинення освітлення вони рекомбінують, так що їх концентрація поступово зменшується за експоненціальним законом(4.39). Під впливом електричного поля, створеного джерелом з напругоюU0, нерівноважні носії прискорюються у напрямку дії сил поля, створюючи у колі струм(його називають
фотострумом).
