Лаб №1 (методичка)
.pdfЛабораторна робота №1
Аналіз і обробка зображень із використанням MATLAB Image Processing Toolbox
Мета: Метою даної лабораторної роботи є утворення основних навичок роботи із зображеннями в додатку Image Processing Toolbox середовища MATLAB.
Вступ
Значну частину даних, що передаються в сучасних системах передавання інформації, насьогодні становлять нерухомі зображення й відео. У зв'язку із цим, знайомство з методами представлення, аналізу, обробки й передавання зображень і відео, як одного з типів інформації, має дуже важливе значення при вивченні принципів побудови й проектування систем зв'язку взагалі, і поліграфії, зокрема.
Надзвичайно зручним і гнучким інструментом для розв'язку перерахованих завдань є пакет Image Processing Toolbox середовища
MATLAB.
Що таке Image Processing Toolbox?
Додаток Image Processing Toolbox являє собою набір функцій, які розширюють можливості моделювання в середовищі MATLAB. Додаток Image Processing Toolbox підтримує різні операції обробки зображень, включаючи:
просторові перетворення зображень;
лінійну й нелінійну фільтрацію зображень;
аналіз і покращення зображень;
відновлення зображень;
стиснення (компресію) зображень;
1. Представлення цифрових зображень
Зображення можна представити як двовимірну функцію f (x, y) , де x і y –
це просторові координати (на площині), а f - амплітуда (яскравість, інтенсивність) зображення в точці з координатами (x, y).
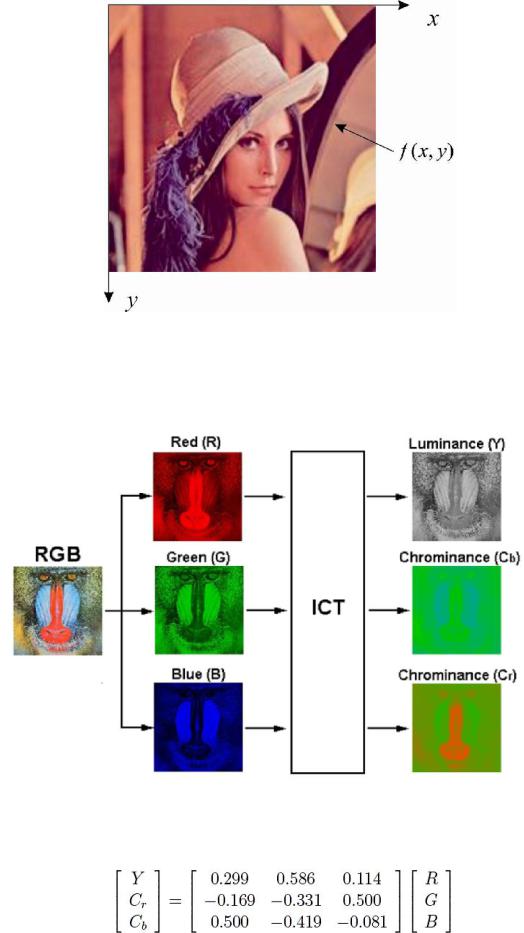
Кольорові зображення являють собою комбінацію з декількох (зазвичай з трьох) монохромних зображень. Наприклад, у колірній системі RGB – це червона, зелена й синя компоненти, у системі YUV – це яскравістна й дві кольороворізницевих компоненти.
Зв'язок між представленнями повнокольорового зображення в різних колірних схемах можна записати в матричній формі:
(1)
Для зворотного перетворення YUV у кольори RGB потрібно звернути матрицю ICT і підставити її у відповідну матричну форму.
Природні зображення (світлини, кіно) зазвичай носять неперервний характер – координати x, y і яскравість f для них можуть приймати будь-які значення. Під час передавання таких зображень крізь цифрові канали зв'язку, а також при зберіганні й обробці в цифровому вигляді, такі зображення повинні бути дискретизовані за просторовими координатами й за рівнем (дискретизація й квантування).
При цьому координати x,y точок зображення, а також значення яскравості f стають дискретними - xi, yj і fq(xi, yj).
Таке зображення називається цифровим. А значення елемента зображення називається "піксель" - це скорочено від "picture element".
2. Зображення в MATLAB і Image Processing Toolbox
Основною структурною одиницею даних в MATLAB є масив. Для представлення зображення дані в масиві повинні нести інформацію про значення інтенсивностей зображення.
MATLAB запам'ятовує зображення у вигляді двовимірного масиву (тобто матриці розміром M×N), у якому кожний елемент з координатами (x,y) відповідає одному пікселю зображення.
Координати пікселів x і y можуть приймати цілі значення від 1 до M і від 1 до N, відповідно.
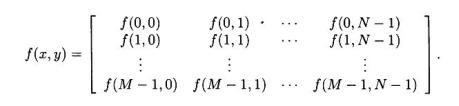(2) Наприклад, якщо зображення складається з 200 рядків і 300 стовпчиків, то воно в системі MATLAB запам'ятовується у вигляді матриці розмірністю
200×300.
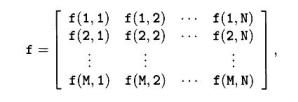
Повнокольорові зображення представляються у вигляді тривимірних масивів (наприклад – RGB), де є червона, зелена й синя складові.
Індексація масивів в MATLAB починається з одиниці, тому відповідна матриця в MATLAB буде мати вигляд
(3)
2.1. Зчитування зображень
Зображення, що підлягають обробці в MATLAB зберігаються у файлах, тому першою дією при роботі із зображенням є його завантаження в програму. Очистимо робочий простір MATLAB від усіх змінних і закриємо відкриті вікна відображень.
clear, close all
Для зчитування зображень використовується функція imread.
У цьому прикладі показане зчитування одного зображення pout.tif, яке включено в додаток Image Processing Toolbox, і його запам'ятовування у вигляді масиву I.
I = imread('pout.tif');
Для зчитування зображення, розташованого в деякій конкретній папці потрібно в явному вигляді вказати повний шлях до цієї директорії, наприклад:
f = imread('D:\Myimage\rose.jpg');
У першому прикладі функція imread зчитує дані з графічного формату TIFF (Tagged Image File Format), у другому – JPEG.
Список деяких найбільш відомих підтримуваних форматів наведений нижче:
|
BMP |
Windows Bitmap |
|
GIF |
Graphics Interchange Format |
|
HDF |
Hierarchical Data Format |
|
JPEG, JPG |
Joint Photographic Experts |
|
PBM |
Portable Bitmap |
|
PCX |
Paintbrush |
|
PGM |
Portable Graymap |
|
PNG |
Portable Network Graphics |
TIFF, TIF |
Tagged Image File Format |
Функція imread дозволяє зчитувати зображення із графічних файлів різних форматів і з різною глибиною кольору (кількість біт на піксель у кожному колірному компоненті). Більшість форматів використовує для запам'ятовування значень пікселів 8 біт на піксель.
Якщо ці дані зчитуються у пам’ять, то система MATLAB запам'ятовує їх у форматі uint8.
Для файлових форматів PNG і TIFF, які підтримують 16-бітні дані, система MATLAB запам'ятовує зображення у форматі uint16.
2.2. Інформація про зображення
Після зчитування зображення корисно одержати інформацію про нього. Зокрема, дуже часто потрібна інформація про розмір зображення (кількість пікселів по вертикалі й по горизонталі). Зробити це можливо за командою:
size(I)
Відповіддю програми буде:
ans = |
291 240. |
Більш повну інформацію про зображення можна одержати за командою:
whos I
Відповіддю, у цьому випадку, буде не тільки інформація про розмір зображення в пікселях, але й про ім.’я масиву, його розмір і клас даних, що містяться в ньому.
Name |
Size |
Bytes |
Class |
Attributes |
I |
291x240 |
69840 |
uint8 |
|
2.3. Типи зображень
Пакет Image Processing Toolbox працює з наступними типами зображень:
-півтонові зображення (зображення в градаціях сірого);
-двійкові (чорно-білі) зображення;
-кольорові зображення RGB.
Півтонові зображення
Півтонове зображення – це матриця, елементи якої представлені у вигляді числових значень класів uint8 [0,255], або uint16 [0,65535].
Двійкові зображення
Двійкові зображення в MATLAB являють собою матрицю логічних елементів 0 або 1. Для перетворення числових масивів у логічні слугує
функція logical - B=logical(A)
Повнокольорові зображення
Повнокольорові зображення являють собою такий тип зображень, де кожний піксель описується трьома значеннями червоної, синьої й зеленої складових. Система MATLAB запам'ятовує повнокольорові зображення у вигляді масиву даних з розмірністю m×n×3. У цьому масиві зберігається кожний компонент кольору для кожного окремого пікселя.
Графічний файловий формат запам'ятовує повнокольорові зображення як 24-бітні дані, де червоний, зелений і синій компонент представлено 8 бітами кожний. У сумі це дає близько 16 мільйонів кольорів. Повнокольорові зображення можуть бути представлені у форматах uint8, uint16, single
або double.
2.4. Виведення зображення на монітор
Розглянемо питання відображення зчитаного зображення.
Зображення можна вивести на дисплей за допомогою функції imshow, що має наступний синтаксис:
imshow(f, G)
де f – матриця зображення, G – число градацій яскравості, що використовуються для відображення. Якщо параметр G не вказано, то за замовчуванням G = 256.
imshow(I)
Якщо потрібно вивести на монітор послідовно кілька зображень, зробити це можна в такий спосіб:
imshow(I), figure, imshow(f)
Приклад:
clear, close all
I = imread('pout.tif');
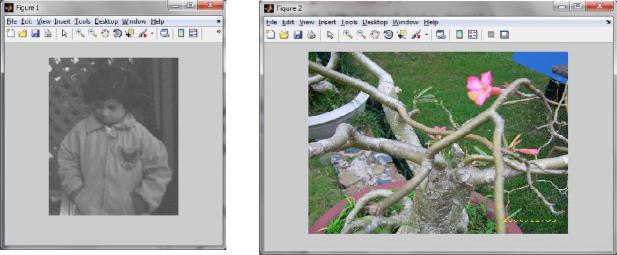
f = imread('D:\Myimage\rose.jpg'); imshow(I), figure, imshow(f)
Результат:
2.5. Збереження зображення.
Зображення записується на диск із використанням функції imwrite, що
має наступний синтаксис:
imwrite(а,'filename')
При цьому, розширення імені файлу filename повинне мати формат, що підтримується MATLAB, наприклад, tif або jpg.
Якщо не зазначений повний шлях до директорії збереження, то збереження проводиться в поточну папку.
3. Найпростіші методи обробки зображень
Процедуру, що забезпечує представлення зображення на екрані ПК або телевізора, називають візуалізацією. При цьому дуже часто характер відображуваного зображення не повною мірою задовольняє користувача. Бажано за допомогою обробки додати виведеному зображенню такі якості, завдяки яким його сприйняття людиною було б по можливості комфортним. Часто буває корисним підкреслити, підсилити якісь риси, особливості, нюанси спостережуваної картини з метою поліпшення її суб’єктивного сприйняття.
3.1. Поелементне перетворення зображень
Однією найпоширеніших дій, що виконуються над зображеннями є так звана поелементна обробка. Тут результат обробки в будь-якій точці зображення залежить тільки від значення зображення в цій самій точці. Перевагою таких процедур є їх гранична простота. Разом з тим, багато з них приводять до очевидного суб’єктивного поліпшення візуальної якості. Цим пояснюється увага, яка приділяється поелементним процедурам.
Сутність поелементної обробки зображень зводиться до наступного. Нехай, x(i,j) і y(i,j) – значення вихідного й обробленого зображень у деякій точці (i,j). Поелементна обробка означає, що існує функціональна однозначна залежність між цими яскравостями
y(i,j)= f x(i,j)
Якщо обробка є однорідною, тобто однаковою для всіх точок зображення, то ця залежність спрощується
y = f(x)
Лінійне контрастування зображення
Контрастність зображення – це співвідношення між найбільш яскравими й найбільш темними ділянками зображення, або його динамічний діапазон за яскравістю. Наприклад, для чорно-білих зображень, що зберігаються у форматі uint8 максимальний динамічний діапазон становить 0 … 255 (0 – рівень чорного, 255 – рівень білого). Насправді не всі зображення мають такий динамічний діапазон. Наприклад, на рисунку, наведеному нижче динамічний діапазон яскравостей становить xmin =180, xmax =240. Зображення в цьому випадку виглядає як ненасичене, незручне, таке, що втомлює під час спостереження.
Завдання контрастування поліпшує узгодження динамічного діапазону
зображення (для розглянутого зображення – 180…240) і пристрою відображення (для відображення у форматі uint8 –0 … 255).
Процедура лінійного контрастування виконується відповідно до виразу y = ax + b
Результат лінійного контрастування для ymin = 0 і ymax = 255 наведений на правому рисунку.
Приведення розподілу яскравостей вихідного зображення до повного динамічного діапазону монітору в MATLAB виконується з використанням
функції – imadjust(I);.
Процедура imadjust(I) обчислює гістограму розподілу яскравостей вихідного зображення (частоту зустрічі тих або інших яскравостей) - histeq, і
потім змінює яскравість кожної точки, віднімаючи від неї константу b = xmin і
домножаючи на коефіцієнт 255/xmax.
Нижче наведений приклад MATLAB коду, що виконує контрастування зображення:
Приклад:
pout = imread('pout.tif'); pout_imadjust = imadjust(pout);
pout_histeq = histeq(pout); figure, imhist(pout) figure, imhist(pout_imadjust)
figure imshow(pout);
title('Вихідне зображення'); figure, imshow(pout_imadjust); title(Контрастоване зображення');
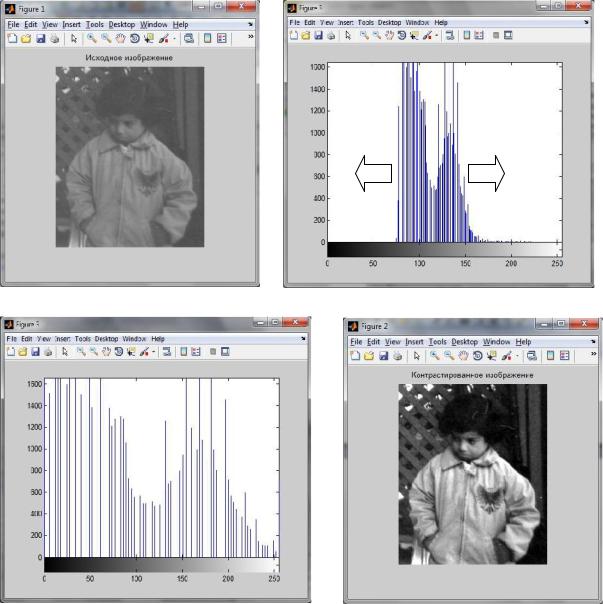
Результат виконання процедури показаний на рисунках.
Вихідне зображення |
Гістограма яскравостей |
Перетворена гістограма |
Контрастоване зображення |
Повний синтаксис функції зміни яскравості зображення y= f(x) - imadjust має вигляд
Imadjust(I, [low_in, high_in], [low_out, high_out], gamma)
де low_in, high_in, low_out, high_out – значення мінімальної й
максимальної яскравості вхідного й вихідного зображень, gamma – закон зміни яскравості в межах діапазону відображення (лінійний, опуклий, увігнутий).
Наприклад, параметри [0,1],[1,0] інвертують значення яскравостей на зображенні, тобто дозволяють одержати негатив вихідного зображення.
Приклад:
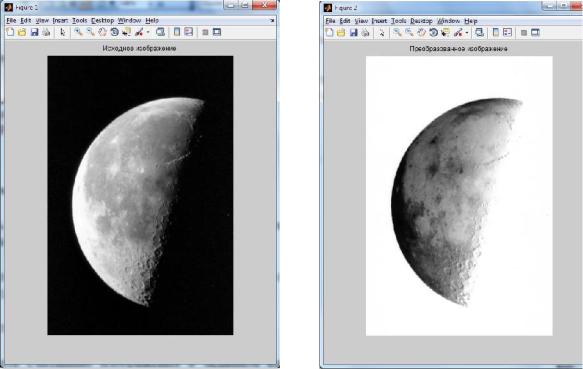
I = imread('moon.tif');
I_imadjust = imadjust(I,[0,1],[1,0],1.5); imshow(I);
title('Вихідне зображення'); figure, imshow(I_imadjust); title('Перетворене зображення');
Іноді зображення, навпаки, мають занадто великий динамічний діапазон яскравостей ( від найтемнішої до найсвітлішої точки), і потрібно його зменшити. Тоді зазвичай застосовують логарифмічне перетворення яскравостей з використанням функції:
g = c*log(1 + f).
При використанні логарифмічного перетворення, дані - f, що мають,